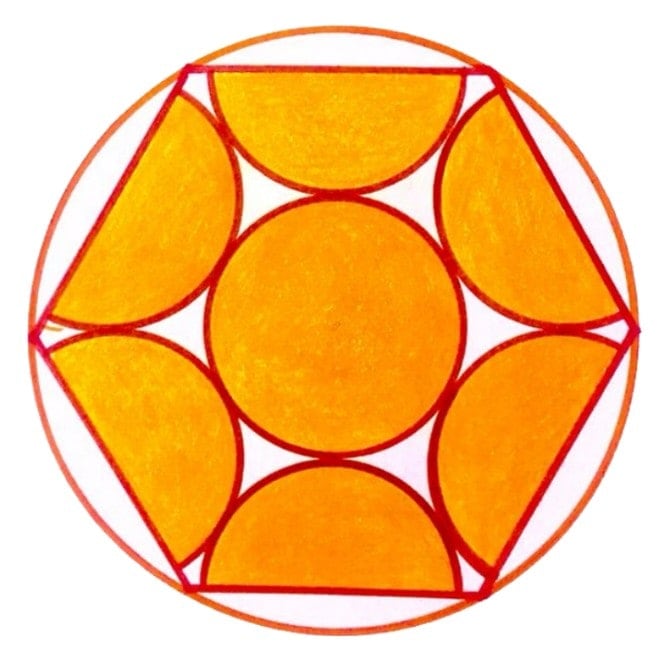
Semicircles in a Hexagon in a Circle

Six equal semicircles (and a circle) sitting in a regular hexagon. What fraction of the outer circle is shaded?

Let the radius of the large circle and the sides of the hexagon have lengths equal to 1. Then, using the Pythagorean Theorem, we see that the lengths of the perpendiculars from the center of the hexagon to its sides are equal to \sqrt{3}/2, and that the radius of a small circle has a length of \sqrt{3}/4. Therefore, the total orange area is 3π/4 which is 75\% of the area of the large circle.