Equilateral Triangles in a Rectangle

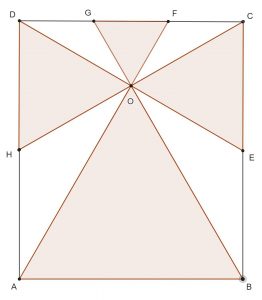
All four triangles are equilateral. What fraction of the rectangle do they cover?

Let the rectangle be ABCD and the four equilateral triangles be ABO, ECO, DGO, DHO.

Because of symmetry, we can see that:

\angle BOE = \angle COF = \angle GOD = \angle HOA.

Therefore, triangles △BCO, △CGO, △FDO, △DAO, △DEC, △HCD are 30°-60°-90°, and

S(BEO)=S(ECO)=S(DHO)=S(HAO),

S(CFO)=S(FGO)=S(GDO).

Thus, if set S(FGO)=S, we find

S(BEO)=S(ECO)=S(CDO)=S(DHO)=S(HAO)=3S,

and

S(ABO)=S(DAO)+S(BCO)-S(CDO)=9S.

Finally, the answer is (9S+3S+3S+S)/24S=2/3.