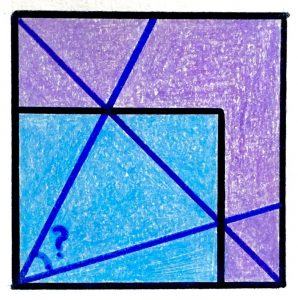
A Rectangle Inside a Square

The blue rectangle covers half of the square’s area. What’s the angle?

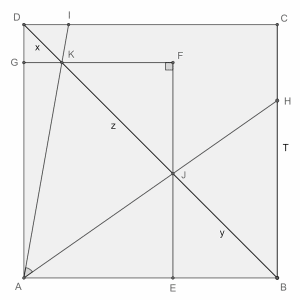
Let the square be ABCD and the rectangle be AEFG. Let EF and FG intersect BD in points J and K. We denote by x, y, z, T the lengths of DK, KJ, JB, BC respectively.

From S(ABD)=S(AEFG), we get that S(KDG)+S(BJE)=S(KJF), and since △KDG, △BJE, △KJF are 90°-45°-45°, we find that:

x^2+y^2=z^2.

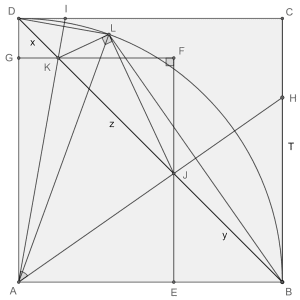
Using the Pythagorean Theorem, we choose a point L inside △BCD, such that KL=x and KL=y, and △KJL is right-angle.

We have

∠DKL+∠LJB=360°-LKJ-KJL=270°,

so using that △JBL and △DKL are isosceles, we get:

∠BLD=90°+∠KLD+∠BLJ=270°-∠DKL-∠LJB=135°.

Thus, the point L lies on the circle with center A and radius AB, and AD=AL=AB. Then, we see that AK and AJ are bisectors of ∠DAL and ∠LAB respectively. We conclude:

∠KAJ=∠KAL+∠LAJ=\frac{∠DAL+∠LAB}{2}=45°.