Raymond Merrill Smullyan (1919 – 2017) was an American mathematician, magician, concert pianist, logician, Taoist, and philosopher. Born in Far Rockaway, New York, his first career was stage magic. He earned a BSc from the University of Chicago in 1955 and his Ph.D. from Princeton University in 1959. He is one of many logicians to have studied with Alonzo Church.
If you make a CORRECT statement, you will get either a lollipop or a chewing gum. If you make a FALSE statement, you will get either a chocolate or a car. What statement should you make in order to get the car?
You should say “I will receive a chocolate”. This statement cannot be correct, since if it was, you would get a lollipop or a chewing gum, not a chocolate. Therefore, you will get the car.
You encounter three Gods in a room – the God of Truth, the God of Lie and the God of Uncertainty. You don’t know which one is which, but know that the God of Truth always says the truth, the God of Lie always says the lie and the God of Uncertainty sometimes lies and sometimes says the truth. You can ask in succession each of the Gods a unique question, to which they can reply only with “Yes” or “No”. However, their responses will be in their native language – “Da” or “Ne”, and you don’t know which translation to which answer corresponds. Your task is to figure out what questions to ask the Gods, so that will recognize which one of them is the God of Truth, which one is the God of Lie and which one is the God of Uncertainty.
Label the gods with numbers – 1, 2, and 3.
First, ask god 1 “If I ask you whether god 2 is random, would you say ‘Da’?”. If he responds “Da”, then god 3 is not the god of uncertainty. If he responds “Ne”, then god 2 is not the god of uncertainty. In both cases we will be able to find a god which is not the god of uncertainty, let without of generality that is god 3.
Next, ask god 3 “If I ask you whether you are the God of Lie, would you say ‘Da’?”. If he says “Da”, then he is the God of Truth. If he says “No”, then he is the God of Lie.
Finally, ask god 3 whether god 1 is the God of Uncertainty and conclude the identities of all gods.
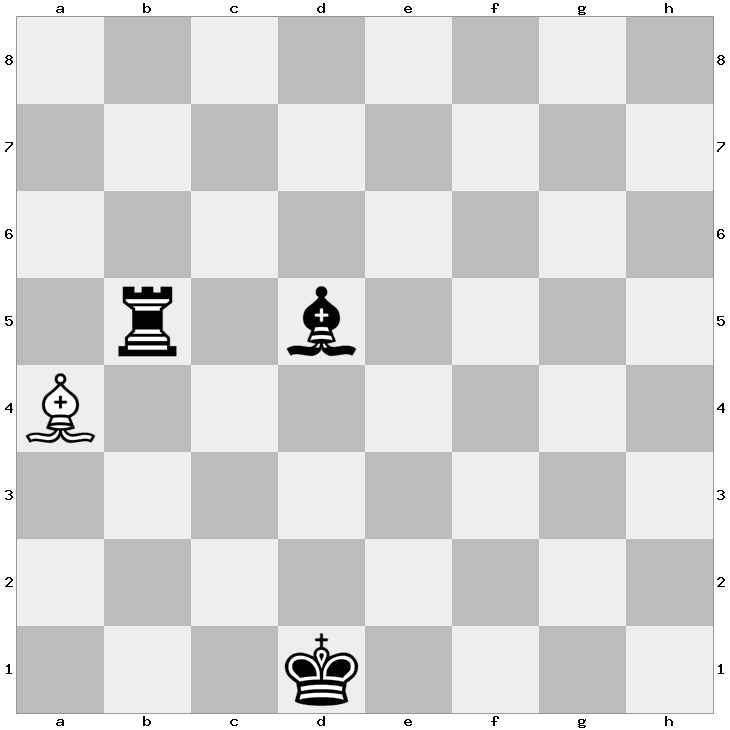
The white king has made himself invisible. Where is he?
The white king is on c3. Since he cannot be currently on b3 (he will be in double check from the black rook and the black bishop), Black must be currently in check from the white bishop. That’s possible only if White has given a discovered check with his king. That’s possible only if on the previous move, the white king was on b3 and was in double check. The only possible way for this to happen is if Black gave two discovered checks at the same time. The one way to do this is if a black pawn on b4 captured a white pawn on c3 using en passant. Thus after b4xc3, the white king has just captured the black pawn on c3, and that is where he is currently hiding.
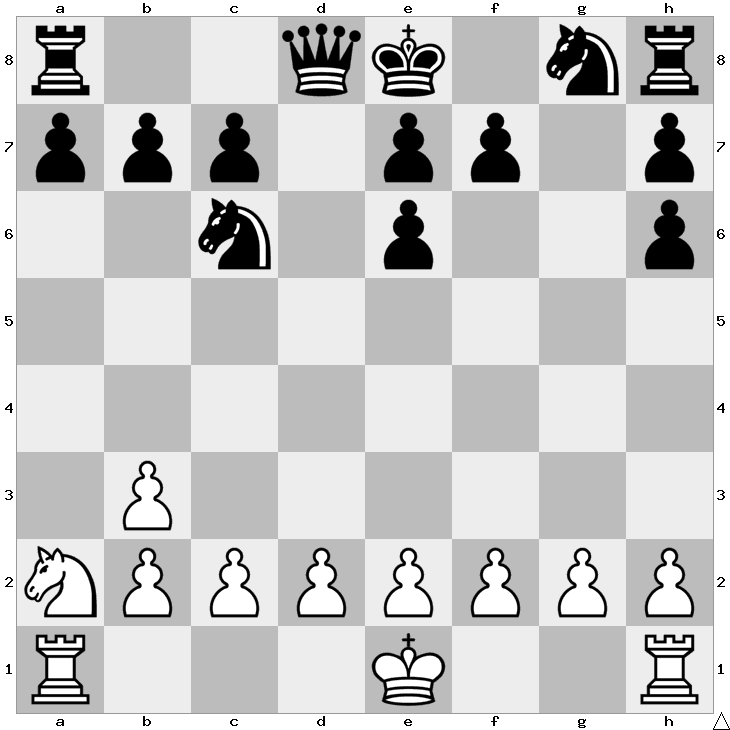
On which spot was the white queen captured?
Since the pawns on e6 and h6 have taken 2 of the White’s pieces, and the only two white pieces which could get there are the knight and the queen, the answer is one of these two squares. Similarly, the pawn on b3 should have taken the Black’s c8 bishop, and this should have happened before the White’s queen was taken. Therefore first the white knight was taken on e6, then the black bishop on b3, and finally the white queen on h6.
Please confirm you want to block this member.
You will no longer be able to:
Please note: This action will also remove this member from your connections and send a report to the site admin. Please allow a few minutes for this process to complete.
