Mammals in Cages
You walk into a room where there are three mammals held in cages:
- a trained dog doing tricks
- a monkey playing with blocks
- a lab rat traversing a maze
Which is the most intelligent mammal in the room?
SOLUTION
The answer is… YOU.
Unknown Author
We do not know where this puzzle originated from. If you have any information, please let us know via email.
We do not know where this puzzle originated from. If you have any information, please let us know via email.
Rabbits, Owls, and Bears
If:
- RABBIT → FROG
- OWL → WOLF
- BEAR → SHEEP
- MOOSE → COW
then BUCK → ?
SOLUTION
The answer is CHICKEN.
RABBIT sounds like the noise a FROG makes, OWL sounds like the noise a WOLF makes, BEAR sounds like the noise a SHEEP makes, and MOOSE sounds like the noise a COW makes. Since BUCK sounds like the noise a CHICKEN makes, that’s the answer.
Pun Riddles
- Why do people go to the corner of the room when they are cold?
- Why was everyone afraid of Albert Einstein’s brother, Frank?
- What subject does a witch teach at school?
- What room can’t a skeleton enter?
- What rock group has only four members and none of them sing?
- What has two butts and kills people?
- How many tickles does it take to make a squid laugh?
- What do you call a squad of babies?
- What is a geologist’s favorite music genre?
- What’s blue and not very heavy?
SOLUTION
- Because it is 90 degrees there.
- Because he was Frank-Einstein, a monster.
- Spell-ing.
- The living room.
- Mount Rushmore.
- An assassin.
- Ten-tickles.
- An infantry.
- Rock.
- Light blue.
Sum Up to 999
Can you find a triple of three-digit numbers that sum up to 999 and collectively contain all digits from 1 to 9 exactly once? How many such triples are there? What if the sum was 1000?
SOLUTION
There are exactly 180 such triples that sum up to 999 and none that sum up to 1000.
In order to see that, notice that the sum of the first digits of the numbers can be no more than 9. Since the sum of all digits is 45, the sum of the middle and the sum of the last digits should be both no more than 9+8+7=24, and no less than 45-9-24=12. We then see that the sum of the last digits should be exactly 19 and the sum of the middle digits should be exactly 18. The sum of the first digits should be 45-19-18=8.
There are 2 ways to get 8 using unique digits from 1 to 9: 1+2+5 and 1+3+4.
- If the first digits are {1, 2, 5}, the options for the middle digits are {3, 6, 9}, {3, 7, 8}, and {4, 6, 8}. The last digits end up {4, 7, 8}, {4, 6, 9}, and {3, 7, 9} respectively.
- If the first digits are {1, 3, 4}, the options for the middle digits are {2, 7, 9} and {5, 6, 7}. The last digits end up {5, 6, 8} and {2, 8, 9} respectively.
Since the set of the first digits, the set of the middle digits, and the set of the last digits of the numbers can be permuted in 6 ways each, we get a total of 5×6×6×6=1080 solutions, or 180 up to permutation of the 3 three-digit numbers.
In order to see that we cannot get a sum of 1000, we note that since the sum of the digits from 1 to 9 is divisible by 9, then the sum of the 3 three-digit numbers should be divisible by 9 as well. Since 1000 is not divisible by 9, the statement follows.
FEATURED
A Broken Circle
There are N points on a circle. If we draw all the chords connecting these points and no three of them intersect at the same point, in how many parts will the interior of the circle get broken?
For example, when N is equal to 1, 2, 3, 4, and 5, we get 1, 2, 4, 8, and 16 parts respectively.
SOLUTION
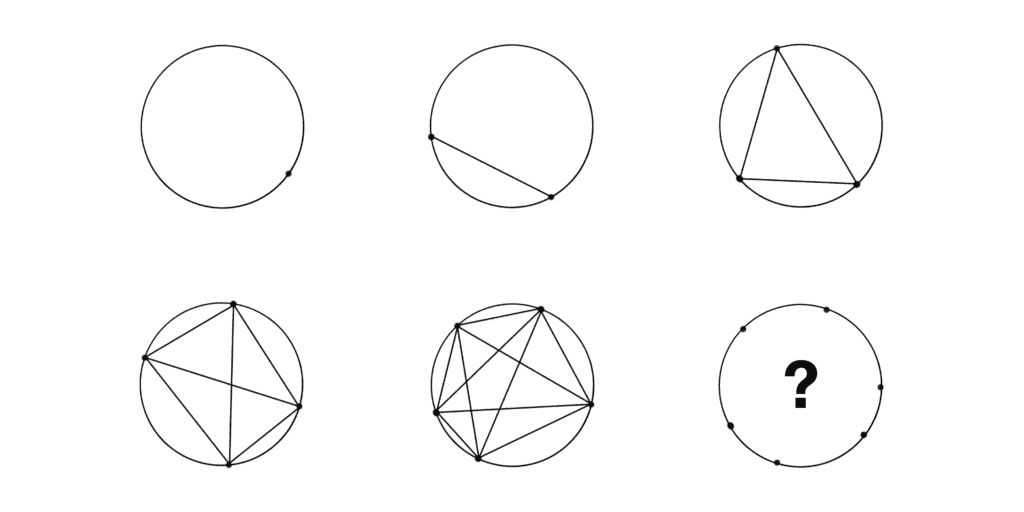
The answer, somewhat surprisingly, is not 2ᴺ⁻¹, but 1 + N(N-1)/2 + N(N-1)(N-2)(N-3)/24.
In order to see that, we start with a single sector, the interior of the circle, and keep successively drawing chords. Every time we draw a new chord, we increase the number of parts by 1 and then add 1 extra part for each intersection with previously drawn chords.
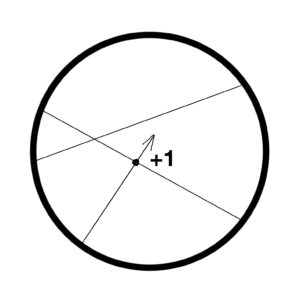
Therefore, the total number of parts at the end will be:
1 + the number of the chords + the number of the intersections of the chords
Each chord is determined by its 2 endpoints and therefore the number of chords is N(N-1)/2.
Each intersection is determined by the 4 endpoints of the two intersecting chords and therefore the number of intersections is N(N-1)(N-2)(N-3)/4!.
Discs, Planets, and Time
Which of the following is the odd one out and why?
- CD
- Venus
- Clock
- DVD
- Mars
- Watch
SOLUTION
The answer is Mars, since it spins counter-clockwise. All the other objects spin (or contain elements that spin) clockwise.
FEATURED
The Bicycle Problem
If you pull straight back on a pedal of a bicycle when it is at its lowest position, will the bicycle move forward or backward?
SOLUTION
The surprising answer is that (usually) the bicycle will move backward.
When a bicycle moves forward, the trajectory its pedal traces with respect to the ground is called a trochoid. Depending on the selected gear of the bicycle, that trochoid could be:
- Curtate trochoid (for almost all gears of most bicycles)
- Prolate trochoid (if the gear is very low and the bicycle moves slowly)
- Common trochoid, a.k.a. cycloid (if the wheels of the bicycle and the pedal spin at identical speeds, practically never happens)
Since we are fixed with respect to the ground, by pulling the pedal backward, we are causing it to move leftward along the trochoid and therefore the bicycle will be moving backward. We note that despite that, the pedal will be moving forward with respect to the bicycle (but not with respect to the ground).
You can see a visual explanation of this puzzle in the video below.
We Go on Vacation
For this puzzle/game, you will need to find a group of friends, preferably 5 or more. The premise is that you will go together on a vacation but each of you can bring only specific items there. The rules regarding which items can be brought and which not are known by one of the players and the other ones are trying to guess them.
In the exchange below, George is the one organizing the trip and the one who knows which items the rest are allowed to bring.
GEORGE: I will take my guitar with me. What do you want to take?
SAM: Can I take an umbrella with me?
GEORGE: No, you cannot take an umbrella, but you can take some sunscreen.
HELLEN: Can I take a scarf with me?
GEORGE: No, you cannot take a scarf, but you can take a hat.
MONICA: Can I take a dress with me?
GEORGE: No, you cannot take a dress, but you can take some makeup.
Can you guess what the rules of the game are?
SOLUTION
Everyone is allowed to take with themselves only items whose first letter is the same as the first letter of their names. Thus, George can take a Guitar, Sam can take Sunscreen, Hellen can take a Hat, and Monica can take Makeup.
Leave No Squares
How many matchsticks do you need to remove so that no squares of any size remain?
SOLUTION
Nine matchsticks are enough, as seen from the solution below.
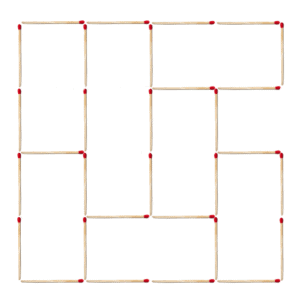
To see that eight matchsticks are not enough, notice that removing an inner matchstick reduces the number of 1×1 squares at most by 2. Since there are 16 such small squares, in order to get rid of them all, we need to remove only inner matchsticks. However, in this case, the large 4×4 square will remain.
The Least Spoken Language
Which is the least spoken language in the world?
SOLUTION
The answer is THE SIGN LANGUAGE.