Do Not Mate!
Find a move for White, which does not result in a mate.

The move is Rc6+. Then Black can play Rxh7.
Find a move for White, which does not result in a mate.

The move is Rc6+. Then Black can play Rxh7.
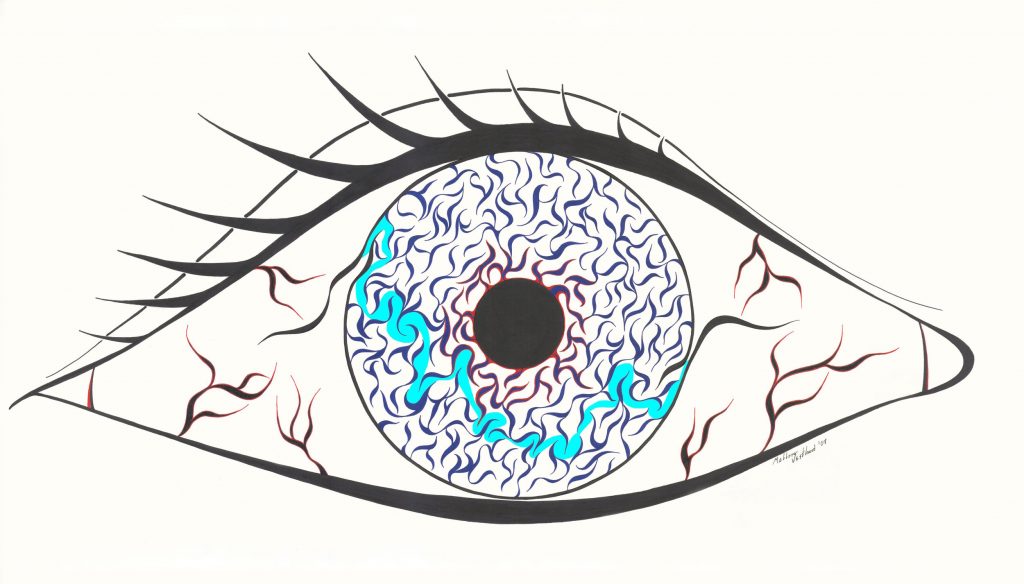
Enter through one side of the iris and exit via the other.
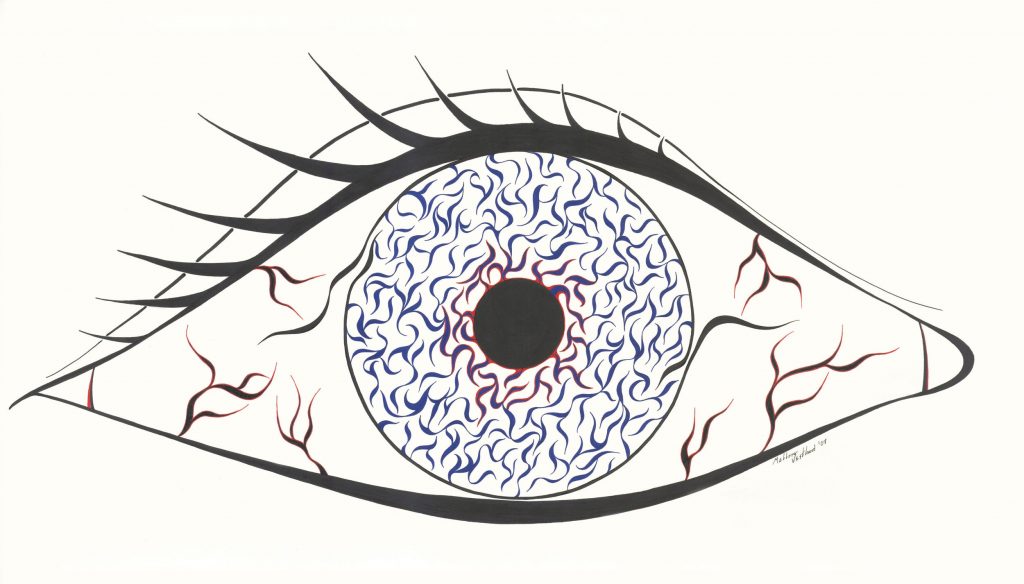
The solution is shown below.
What is correct to say – “the yolk of the egg is white” or “the yolk of the egg are white”?
Neither – the yolk of the egg is yellow.
Can you draw a brain in just 3 seconds? Probably not, at least unless you use some help from Google. AutoDraw by Google Creative Lab is an AI experiment, which lets you make a quick doodle, then tries to guess what it is, and complete it. It does not always work, but it keeps improving and is fun to play with. Also, it shows the powerful capabilities of machine learning. To try
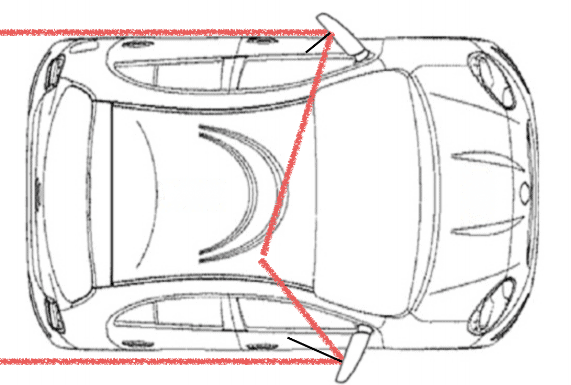
Where is the driver sitting in this car?
Using the positioning of the mirrors, you can conclude that the driver is sitting on the right.
All integer numbers between 1 and 121 are written in the cells of a square grid with size 11 by 11. Then the product of the numbers in every row and the product of the numbers in every column are calculated. Is it possible that the set of all 11 column products coincides with the set of all 11 row-products?
No, it is not possible. There are 13 prime number between 61 and 121. Since there are only 11 rows, two of them, X and Y, appear in the same row. Now that row is divisible by XY, but clearly, no column is divisible by that number.
A scientist has 9 bottles, exactly one of which contains poison. The poison kills any creature which drinks it within 24 hours. If the scientist has 2 lab mice at his disposal, how can he find which is the poisonous bottle within 2 days only?
Label the bottles B1, B2, B3, … , B9.
The first day he lets the first mouse drink B1, B2, B3, and let the second mouse drink B1, B4, and B5. If after 24 hours both mice die, then the poisonous bottle is B1. If only one mouse dies, say the first one, then he lets the second mouse drink B2. If it dies, then the poisonous bottle is B2, otherwise, it is B3. Finally, if neither mouse dies, then he lets the first mouse drink B6 and B7, and lets the second mouse drink B6 and B8. If both mice die after 24 hours, then the poisonous bottle is B6. If only one mouse dies, say the first one, then the poisonous bottle is B7. If neither mouse dies, then the poisonous bottle is B9.
In Y-town all crossroads are Y-shaped, and there are no dead-end roads. Is it true that if you start from any point in the city and start walking along the roads, turning alternatingly left and right at each crossroad, eventually you will arrive at the same spot?
Yes, it is true. If you start walking forward, eventually you will end up in a loop. It is easy to see that your entire path, including the starting spot, must belong to this loop. Therefore, eventually you will end up in the starting spot again.
On top of which number is the car parked?

You are looking at the parking lot upside-down. The numbers on the picture are from 85 to 92. The car is parked on top of 87.
Please confirm you want to block this member.
You will no longer be able to:
Please allow a few minutes for this process to complete.