We do not know where this puzzle originated from. If you have any information, please let us know via email.
How can you split a pizza into 11 equal pieces, using just one clock?
The hour and minute hands of a clock overlap exactly 11 times throughout the day. Keeping the clock in the center of the pizza, just make the cuts along the lines defined by the hands during these times.
Which tire does not move when the car turns right?
The answer is THE SPARE TIRE.
52 cards – 2 of clubs to Ace of clubs, 2 of diamonds to Ace of diamonds, 2 of hearts to Ace of hearts, and 2 of spades to Ace of spades – are arranged in a deck. We shuffle them in the following manner:
Show that this method shuffles the deck uniformly, i.e. every permutation has the same chance to appear.
Notice that at all times the cards below the King of spades are shuffled uniformly. Therefore at the end, after we put the King of spades in a random place inside the deck, the entire shuffle will be uniform as well.
You must cover a 7×7 grid with L-shaped triminos and S-shaped tetrominos, without overlapping (flipping and rotating is permitted). What is the minimum number of pieces you can use in order to do this?
Remark: All pieces must be placed entirely on the board.
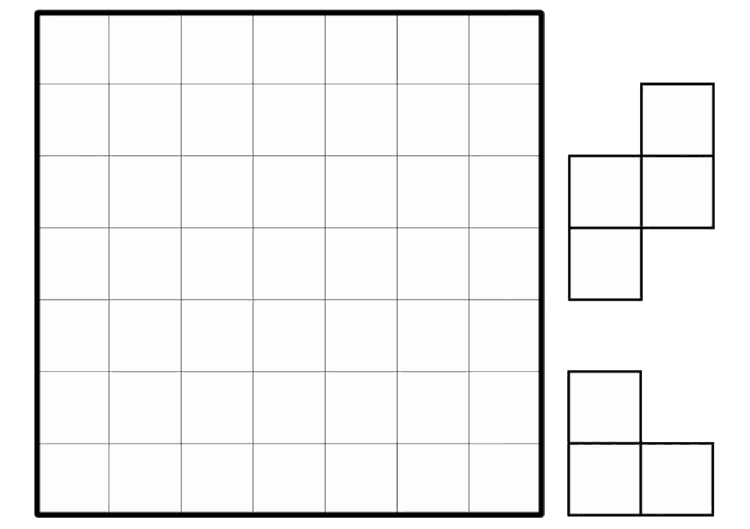
Consider all cells in the grid which lie in an odd row and odd column – there are 16 of them. Since each of the two pieces can cover at most 1 of these cells, we need at least 16 pieces. Giving an example with 16 pieces is easy.
One day, the warden of a prison is, like most wardens in puzzles, feeling a little capricious and decides that he wants to get rid of his prisoners, one way or another. He gathers all the prisoners in the yard and explains to them – “Tonight, I will go to each of you, hand you a key, and tell you who has your key. Each day after that, while the others are out of the cells and no one is watching, I will allow each of you to place your key in someone else’s cell – and each night, you may collect the keys in your own cell. If at any point, you are certain that everyone has the key to their own cell, you may summon me, at which point each of you will open your own cell and walk free. If anyone has the wrong key, everyone will be executed then and there. You may discuss your strategy before tonight, but afterward
That night, just as promised, the warden went to each cell and gave each prisoner a key. As he handed each prisoner the key, he whispered to them the name of the person possessing the key to their cell. The keys were entirely indistinguishable from one another, but that was okay, because the prisoners had not counted on being able to tell anything about them. Indeed, the prisoners all seemed confident.
What was their strategy? How could they beat the warden’s game?
We assume the cells in the prison are arranged in a circle. The prisoners agree every day each of them to pass the key they receive to their left neighbor, except for their own key which they keep. It is easy to figure out which key is their own since they can easily calculate when they will receive it. For example, if prisoner 8 knows that his key is at prisoner 3 in the beginning, then he will get it on the 5th day. Therefore, within 10 days, all prisoners will have their own keys.
A boat has a ladder with six rungs on it. The rungs are spaced one foot from each other, the lowest one starting a foot above the water. The tide rises with 10 inches every 15 minutes.
How many rungs will be still above the water 2 hours later?
Six rings – the ship and the ladder will be rising with the tide.
In one house deep in the forest
The seventh dwarf is also playing chess; 2 people are needed for this.
There are 10 birds on a tree. One hunter shoots at them and hits 2. How many birds are left on the tree?
Zero – the remaining 8 birds get scared and fly away.
Between every pair of major cities in Russia, there is a fixed travel cost for going from either city to the other. Traveling salesman Alexei Frugal starts in Moscow and visits all cities exactly once, choosing every time the cheaper flight to a city he has not visited so far. Salesman Boris Lavish starts in St Petersburg and visits all cities exactly once, choosing every time the most expensive flight to a city he has not visited so far. Can Alexei end up spending more money than Boris after they end their journeys?
No, it is impossible. For every trip of Alexei we will choose a trip of Boris, which costs at least as much.
Let the number of cities is n and Alexei visits them in order 1 -> 2 -> … -> n.
If Boris visits city n-1 before city n, then pair Alexei’s trip (n-1, n) with Boris’ trip (n-1, #). Notice that C(n-1, n) < C(n-1, #).
If Boris also visits city n-2 before city n, then pair Alexei’s trip (n-2, n-1) with Boris’ trip (n-2, #). Notice that C(n-2, n-1) < C(n-2, n) < C(n-2, #).
Continue like this until get to a city k which Boris visits after city n. Then pair Alexei’s trip (k, k+1) with Boris’ trip (n, #). Notice that C(k, k+1) < C(k, n) < C(n, #).
Next, check whether Boris visits city k – 1 before city k, and pair Alexei’s trip (k-1, k) with either (k-1, #) or (k, #). Continue like this, until pair all of Alexei trips with more expensive Boris trips.
Please confirm you want to block this member.
You will no longer be able to:
Please note: This action will also remove this member from your connections and send a report to the site admin. Please allow a few minutes for this process to complete.
