Birthday Candles
If 10 Birthday candles burn out in 8 minutes, in how many minutes will 15 Birthday candles burn out?
Every candle burns out in 8 minutes, so the answer is 8.
We do not know where this puzzle originated from. If you have any information, please let us know via email.
If 10 Birthday candles burn out in 8 minutes, in how many minutes will 15 Birthday candles burn out?
Every candle burns out in 8 minutes, so the answer is 8.
In what color is “2016” written below?

You can not see 2016, so it must be written in white color.
Which is the next symbol in the following sequence?

This is the sequence 1, 2, 3, 4, 5… with all numbers stuck to their mirrored images.
Each night one of three prisoners has steak for dinner, while the other two have fish tacos. Also every night, each of the three prisoners votes for one of the following two options:
If a majority go with option 2, nothing happens that night. If a majority go with option 1, then they are set free if they are right and executed if they are wrong. The distribution of votes is kept secret, so it is unknown what each of the others voted. Also, it is known that every prisoner eventually will get a steak.
The three prisoners can have a brief strategy meeting and after that, they are not allowed to communicate. What should the prisoners’ strategy be?
The prisoner who gets a steak the first night should always vote 2, whereas the other two prisoners should vote 2 until the night they get a steak, and 1 every night after.
Can you move just one card so that you get a correct identity?
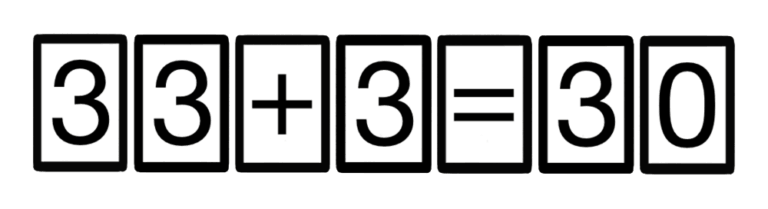
Yes, you can, as shown below.

You have 10 unlimited piles of balls and one digital scale. All balls in a pile have the same weight, which is an integer between 1 and 9 grams. How many measurements do you need in order to find the weight of the balls in every pile?
You need only one measurement – take 1 ball from pile 1, 10 balls from pile 2, 100 balls from pile 3, etc., and measure their total weight. The first digit of the number shown on the scale determines the weight of the balls in the 10th pile, the second digit determines the weight of the balls in the 9th pile and so on.
Why are manholes round?
Because it is impossible for the covers to drop inside the holes, no matter how you position them on top. Also, when they have
Here’s a little maze puzzle I originally built a couple of years ago, that seems apropos to reprise now:

Can you make it from the A in the top left of this grid to the Z in the bottom right, always going either up one letter (for instance, A to B or G to H) or down one letter (for instance, N to M)? The alphabet wraps around, so you can go from Z up to A or A down to Z too. Try as hard as you can (and remember that you can always work backward if you get stuck forwards), and see where you get!
Remark: Solving the maze is not the same thing as solving the puzzle. Read those instructions carefully!
Notice this puzzle is published on April 1st. Actually, it doesn’t have a standard solution. If you connect every two consecutive letters which appear next to each other in the grid, you will get two disconnected components, one of which contains the START and the other contains the END. The first component has 5 dead-ends – at letters A, P, R, I, L, and the second component has 5 dead-ends – at letters F, O, O, L, S. These two spell out “April Fools”, which is the real solution of the maze.

This is a map of old-time Kongsberg. The green shapes are bridges which connect the different parts of the city. Can you find a path through the city which goes through every bridge exactly once?
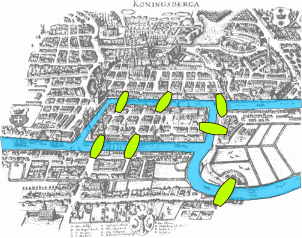
No, you cannot. Notice that, except for the first city and the last city section you finish, the number of bridges used in every other section is even. However, there are three sections with an odd number of bridges, and therefore you cannot use all bridges exactly once.
What is heavier – 1 pound of apples or 1 pound of strawberries?
They are equally heavy – 1 pound each.
Please confirm you want to block this member.
You will no longer be able to:
Please allow a few minutes for this process to complete.