1 to 8 on a Cube
Place the numbers from 1 to 8 on the vertices of a cube so that the sum of the four numbers on every face is the same.
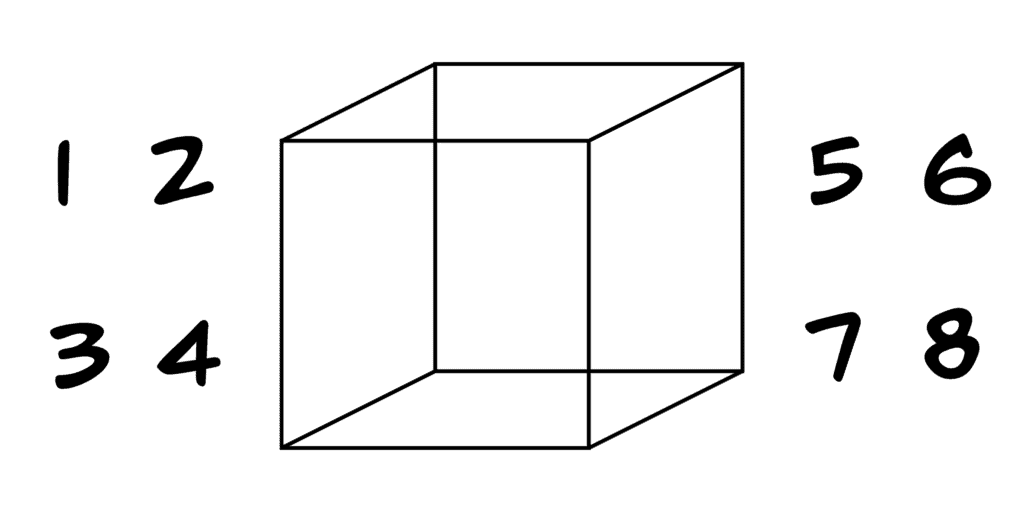
The solution is shown below:
A collection of Math, Chess, Detective, Lateral, Insight, Science, Practical, and Deduction puzzles, carefully curated by Puzzle Prime.
We do not know where this puzzle originated from. If you have any information, please let us know via email.
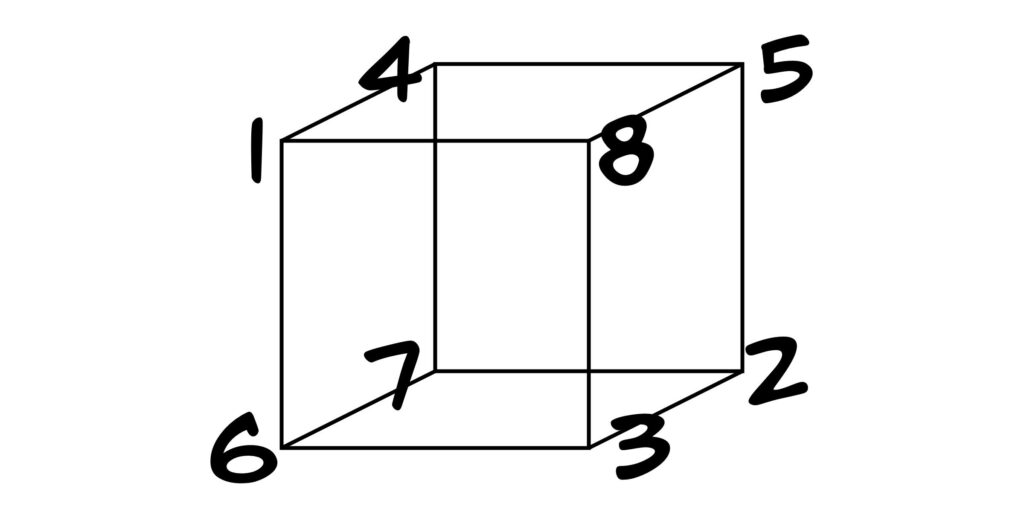
Place the numbers from 1 to 8 on the vertices of a cube so that the sum of the four numbers on every face is the same.

The solution is shown below:

Which is the next number in the following sequence:
1, 3, 7, 12, 18, 26, 35, 45, 56, ?
This is the so called Hofstadter Figure-Figure Sequence.
The sequence of the differences between the consecutive numbers in the original sequence is 2, 4, 5, 6, 8, 9, 10, 11… These are exactly the natural numbers missing from the original sequence. Therefore, the next number should be 56 + 13 = 69.
A cardinal points and says, “thorn, shout, seat, and stew.” Can you explain?
The sentence is a play on words and anagrams. Thorn, shout, seat, and stew are anagrams of the four cardinal directions of the compass: north, south, east, and west.
There are 100 rooms in a row in a building and inside each room there is a lamp that is turned off. One person enters each room and switches the lamp inside. Then, a second person enters every second room (2, 4, 6, etc.) and switches the lamp inside. A third person switches the lamp in every third room and so on and so far, until person #100 switches the lamp in room 100. How many lamps are turned on at the end?
We can see that the only switches that have been switched an odd number of times are the ones in rooms with perfect square numbers.
Indeed, if person N has switched the switch in room M, then person M/N has done that as well. Since person N and M/N coincide only when M=N², the claim above follows.
We conclude that the number of lamps that are turned at the end is equal to the number of perfect squares less than or equal to 100; that is exactly 10 rooms.
What unique feature do the following words share?
FRIEND, FEAST, THERE, THOROUGH, FLIGHT, WONDERFUL, RESIGN, ENDURING, PEST, COVERT
Each of these words contains its antonym as a sub-word:
FRIEND – FIEND, FEAST – FAST, THERE – HERE, THOROUGH – ROUGH, FLIGHT – FIGHT, WONDERFUL – WOEFUL, RESIGN – REIGN, ENDURING – ENDING, PEST – PET, COVERT – OVERT
The numbers 1, 2, … , 100 are arranged in a 10×10 table in increasing order, row by row and column by column, as shown below. The signs of 50 of these numbers are flipped, such that each row and each column have exactly 5 positive and 5 negative numbers. Prove that the sum of all numbers in the resulting table is equal to 0.
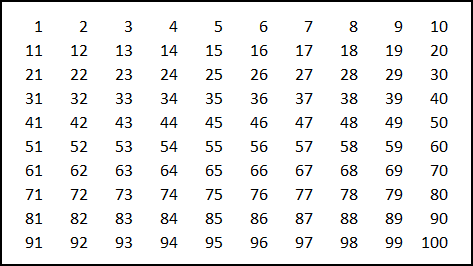
Represent the initial table as the sum of the following two tables:
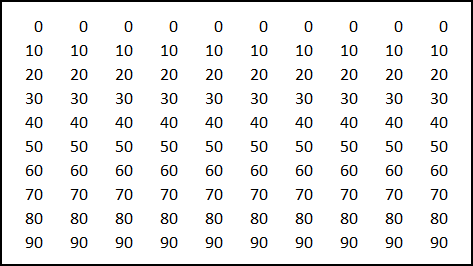

Since the sum of the numbers in each row of the first table is equal to 0 and the sum of the numbers in each column of the second table is equal to 0, it follows that the sum of all numbers in both tables is equal to 0 as well.
Quantum Magazine, November-December 1991
A student was given math homework consisting of the following three problems. What is so special about this homework?
The answer to each of the problems in the homework is hidden within the question itself:
A dog was tied to a tree with a 7-meter rope. How did the dog manage to get to its bowl of food which was 15 meters away from the dog?
The dog was initially on the other side of the tree and the tree’s diameter was 1 meter long. Thus, when the dog moved to the opposite side, it got 2×7+1=15 meters closer to its food.
Find a number containing every digit 0-9 exactly once, such that for every 1≤N≤10, the leftmost N digits comprise a number, divisible by N.
Let the number be ABCDEFGHIJ.
We conclude that the only solution is 3816547290.
How many pawns can you place at most on a chess board so that no three pawns lie on a single line, horizontal, vertical, or diagonal?
Since there are 8 rows on the chess board, if you place more than 16 pawns, then there will be at least 3 that lie on a single horizontal line. An example with 16 pawns is shown below:

Please confirm you want to block this member.
You will no longer be able to:
Please allow a few minutes for this process to complete.