0 > 2, 2 > 5, 5 > 0
0 > 2, 2 > 5, 5 > 0. What is this?
SOLUTION
This is the game “Rock, Paper, Scissors”. Rock (0 fingers) beats scissors (2 fingers). Scissors (2 fingers) beats paper (5 fingers). Paper (5 fingers) beats rock (0 fingers).
Category: Brain Teasers
A collection of Math, Chess, Detective, Lateral, Insight, Science, Practical, and Deduction puzzles, carefully curated by Puzzle Prime.
We do not know where this puzzle originated from. If you have any information, please let us know via email.
Cow and Rope
A cow is tied to a 4 meter long rope. There is food, 20 meters away from the cow. However, the cow manages to go to the food and eat it. How come?
SOLUTION
The rope is not tied to anything but the cow, so the cow is free to go to the food.
The Missing Digit
The number 229 has 9 digits, all different. Which digit is missing?
Bonus: Is the number 9991 prime?
SOLUTION
Let the missing digit be m. Every number and the sum of its digits give the same remainder when divided by 9. The number 229 = 32 * 644 gives remainder 5 when divided by 9, and therefore 9 divides (0 + 1 + 2 + … + 9) – 5 – m = 40 – m. Thus, the missing digit is 4.
Bonus: 9991 = 10000 – 9 = 1002 – 32 = (100 – 3)(100 + 3) = 97 * 103. Therefore the number 9991 is not prime.
Cover the Table
100 coins are placed on a rectangular table, such that no more coins can be added without overlapping. Show that you can cover the entire table with 400 coins (overlapping allowed).
SOLUTION
Since we can not place any more coins on the table, each point of it is at distance at most 2r from the center of some coin, where r is the radius of the coin. Now shrink the entire table twice in width and length, then replace every shrunk coin with a full sized one. This way the small table will be completely covered because every point of it will be at distance at most r from the center of some coin. Add three more of these smaller tables, covered with coins, to create a covering of the big table.
Borromean Rings
Borromean rings are rings in the 3-dimensional space, linked in such a way that if you cut any of the three rings, all of them will be unlinked (see the image below). Show that rigid circular Borromean rings cannot exist.
SOLUTION
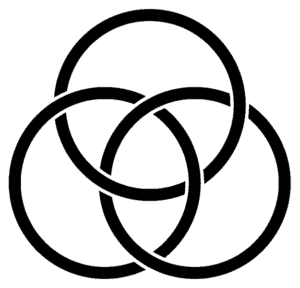
Assume the opposite. Imagine the rings have zero thickness and reposition them in such a way, that two of them, say ring 1 and ring 2, touch each other in two points. These two rings lie either on a sphere or a plane which ring 3 must intersect in four points. However, this is impossible.
Seven Sevens
Seven sevens are given. Find the other digits in this multiplication.
SOLUTION
The answer is:
21817 x 96787 = 2111601979
Fastest Stalemate
Can you design a chess game that ends up with a stalemate in the 10th move?
SOLUTION
One possible game is:
1. h4 h5
2. c4 a5
3. Qa4 Ra6
4. Qxa5 Rah6
5. Qxc7 f6
6. Qxd7 Kf7
7. Qxb7 Qd3
8. Qxb8 Qh7
9. Qxc8 Kg6
10. Qe6
Broken Window
One snowy night, Sherlock Holmes was in his house sitting by a fire. All of a sudden a snowball came crashing through the window, breaking it. Holmes got up and looked out just in time to see three neighborhood kids who were brothers run around the corner. Their names were John Crimson, Mark Crimson
The next day Holmes got a note on his door that read:
“? Crimson. He broke your window.”
Which of the three Crimson brothers should Sherlock Holmes question about the incident?
SOLUTION
He should question Mark. The note read: “QUESTION MARK Crimson. He broke your window.”
Selfmate
White starts and forces Black to mate him in 8 moves.
SOLUTION
1. Nb1+ Kb3
2. Qd1+ Rc23
3. Bc1 axb6
4. Ra1 b5
5. Rh1 bxc4
6. Ke1 c3
7. Ng1 f3
8. Bf1 f2#
WWII Planes
During World War II, the mathematician Abraham Wald was asked to help with determining which parts of the allied forces’ planes must be armored better. After examining the surviving American planes, he noticed that there were many holes in the fuselage, and very few in the engines. After careful thinking, he suggested that the armor on the engines must be improved. Why?
SOLUTION
Abraham Wald realized that the holes should have been distributed more evenly across the planes. Therefore the planes which had more holes in the fuselage survived, while the planes which had more holes in the engines got destroyed.