Brain Teasers 33 - Puzzle Prime

Square Cake

Section: Brain Teasers Category: Mathematics

Difficulty: Medium Tags: Geometry

There is a square cake at a birthday party attended by a dozen people. How can the cake be cut into twelve pieces, so that every person gets the same amount of cake, and also the same amount of frosting?

Remark: The decoration of the cake is put aside, nobody eats it.

SOLUTION

Divide the boundary of the cake into twelve equal parts, then simply make cuts passing through the separation points and the center. This way all tops and bottoms of the formed pieces will have equal areas, and also all their sides will have equal areas. Since all pieces have the same height, their volumes will be equal as well.

Unknown Author January 10, 2020

0 Comments

Cogwheels

Section: Brain Teasers Category: Insight

Difficulty: Medium

There are two cogwheels on a table. The bigger one has 10 teeth and is fixed to the table. The smaller one has 5 teeth and revolves around the bigger one. If the smaller cogwheel makes one full rotation around the bigger cogwheel, how many rotations will it make with respect to the table?

SOLUTION

The answer is three rotations in total. Two because of the ratio 10:5, one more because of the movement of the smaller cogwheel.

Unknown Author January 7, 2020

0 Comments

Mystery Mate

Section: Brain Teasers Category: Chess

Difficulty: Advanced

White plays and mates Black in one move. However, there is a mystery in this position that has to be revealed first.

SOLUTION

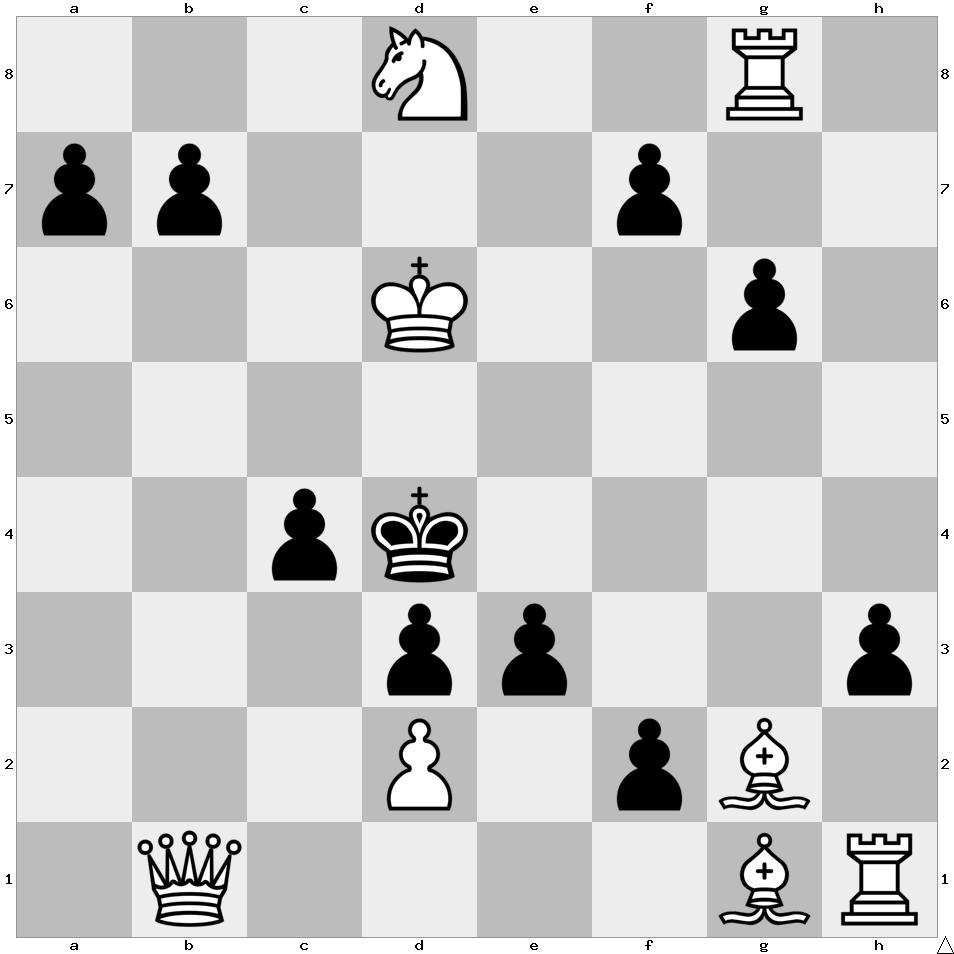
The mystery is that someone has just placed one extra black pawn on the board – there are 9 in total. Also, no matter which one is the added pawn, there always exists a mate in one move.

If the extra pawn was a7 – Qb6
If the extra pawn was b7 – Kc6
If the extra pawn was c4 – Qb4
If the extra pawn was d3 – Qe4
If the extra pawn was e3 – Bxf2
If the extra pawn was f7 – Ke6
If the extra pawn was g6 – Rg4
If the extra pawn was h3 – Rh4

Unknown Author December 28, 2019

0 Comments

Wobbling Table

Section: Brain Teasers Category: Mathematics

Difficulty: Hard

A perfectly symmetrical square 4-legged table is standing in a room with a continuous but uneven floor. Is it always possible to position the table in such a way that it doesn’t wobble, i.e. all four legs are touching the floor?

SOLUTION

The answer is yes. Let the feet of the table clockwise are labeled with 1, 2, 3, 4 clockwise. Place the table in the room such that 3 of its feet – say 1, 2, 3, touch the ground. If foot 4 is on the ground, then the problem is solved. Otherwise, it is easy to see that we can not put it there if we keep legs 2 and 3 in the same places. Now start rotating the table clockwise, keeping feet 1, 2 and 3 on the ground at all times. If at some point foot 4 touches the ground as well, the problem is solved. Otherwise, continue rotating until foot 1 goes to the place where foot 2 was and foot 2 goes to the place where foot 3 was. Foot 3 will be on the ground, but this contradicts the observation that initially we couldn’t place legs 2, 3 and 4 on the ground without replacing feet 2 and 3.

Unknown Author December 25, 2019

0 Comments

Prank the Professors

Section: Brain Teasers Category: Deduction

Difficulty: Medium

Three professors fell asleep under a tree. At some point a prankster passed by and painted their faces with black dye. When the professors woke up, each of them saw the others’ faces and started laughing at them. After a while though, they stopped laughing, realizing that their own faces were painted as well. How did they deduce that?

SOLUTION

Let us denote the professors with A, B and C. The thought process of A would go like this: “If my face is not painted, then B will see that C is laughing at him and will realize immediately that he is being pranked. However, B was laughing for a while and therefore my I must being pranked as well.”. Then A will stop laughing and the same will happen with the other two professors B and C.

Unknown Author December 22, 2019

0 Comments

FEATURED

Repetitive

Section: Brain Teasers Category: Insight

Difficulty: Advanced Tags: Featured, Words

You have two groups of words:

black, word, English, brief, noun, grandiloquent, last
white, number, Russian, long, verb, unpretentious, first

To which group does “repetitive” belong?

SOLUTION

The first group contains self-explanatory words (known as autologicals), the second group does not. Therefore “repetitive” should belong to the first group.

Puzzle Prime December 19, 2019

0 Comments

Chocolate Bar

Section: Brain Teasers Category: Insight

Difficulty: Medium

Louis has a bar of chocolate 4×6 which is marked into 24 little squares. At each step, he breaks up one of its pieces along any of the marked horizontal/vertical lines. Show that no matter how he does that, it will always take the same number of steps until the chocolate is broken into single 1×1 pieces.

SOLUTION

Every time he splits the chocolate, the number of pieces increases by 1. Therefore it will always take him 23 steps to split it into single pieces.

Unknown Author December 13, 2019

0 Comments

Four Points in the Plane

Section: Brain Teasers Category: Mathematics

Difficulty: Advanced Tags: Geometry

Find all configurations of four points in the plane, such that the pairwise distances between the points take at most two different values.

SOLUTION

All 6 configurations are shown below: a square, a rhombus with 60°-120°-60°-120°, an equilateral triangle with its center, an isosceles triangle with 75°-75°-30° and its center, a quadrilateral with 75°-150°-75°-150°, and a trapezoid with base angles of 72°.

Unknown Author December 7, 2019

2 Comments

Guess the Fruits

Section: Brain Teasers Category: Deduction

Difficulty: Medium

You are given 3 boxes – one labeled “Apples”, one labeled “Bananas”, and one labeled “Apples and Bananas”. You are told that the labels on the boxes have been completely mismatched, i.e. none of the three labels is put on its correct box. How can you open just one box and pick a random fruit from it, so that after seeing the fruit, you can guess correctly the contents of every box out of the three?

SOLUTION

Open the box labeled “Apples and Bananas”. If you pick a banana from it, then the box labeled “Bananas” will contain apples, and therefore the box labeled “Apples” will contain apples and bananas. Similarly, if you pick an apple from it, then the box labeled “Apples” will contain bananas, and therefore the box labeled “Bananas” will contain apples and bananas”.

Unknown Author December 4, 2019

0 Comments

Thank You!

Section: Brain Teasers Category: Lateral

Difficulty: Hard

A cowboy walks into a bar and asks the barman for a glass of water. The barman pulls out a gun instead and points it at the man. The man genuinely says “Thank you” and walks out.

What happened?

SOLUTION

The cowboy had hiccups and needed water. The barman shocked him with his gun instead and that cured the hiccups.

Unknown Author December 1, 2019

0 Comments