Shoot, Hang, Dinner
A woman shoots her husband, then holds him under water for five minutes, then hangs him, and finally
The woman takes a picture of her husband and develops it in a dark room.
A collection of Math, Chess, Detective, Lateral, Insight, Science, Practical, and Deduction puzzles, carefully curated by Puzzle Prime.
We do not know where this puzzle originated from. If you have any information, please let us know via email.
A woman shoots her husband, then holds him under water for five minutes, then hangs him, and finally
The woman takes a picture of her husband and develops it in a dark room.
A chess king starts on one cell of a chessboard and takes a non-intersecting tour, passing through each square once, and ending up on the initial square. Show that the king has made no more than 36 diagonal moves.

The king must visit the 28 perimeter squares in order; otherwise, he will create a portion of the board which is inaccessible for him. However, he can not travel from one square to a neighboring one using only diagonal moves. Therefore, he must make at least 28 horizontal/vertical moves and at most 64 – 28 = 36 diagonal moves.
If Black just made a move in this game, what is the minimum amount of moves that have been played?
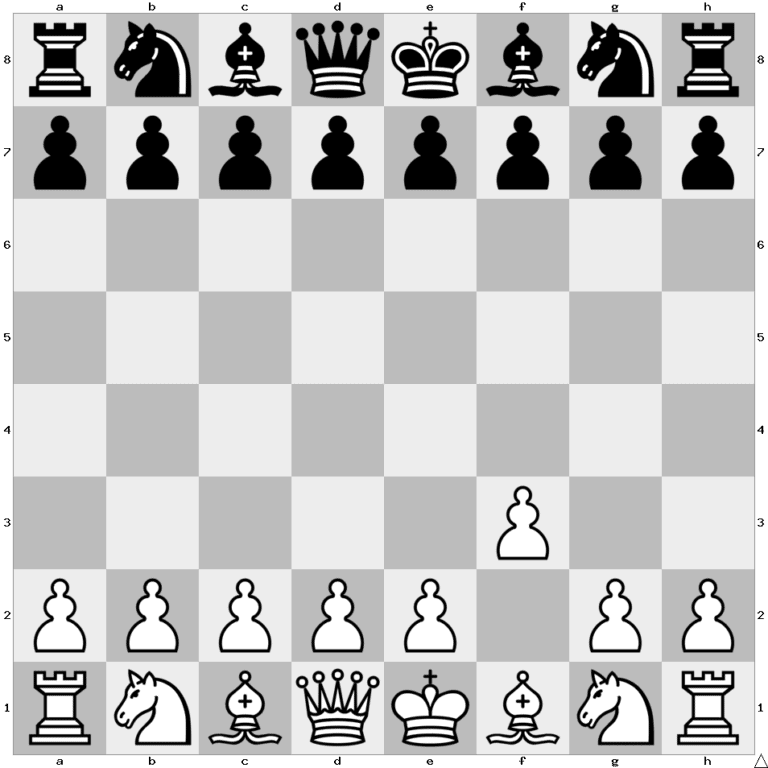
8 moves example:
1. f3 Nf6
2. Kf2 Ng8
3. Ke3 Nf6
4. Kd3 Ng8
5. Ke4 Nf6
6. Ke3 NNg8
7. Kf2 Nf6
8. Ke1 Ng8
In order to see that 8 is the minimum number of moves, notice that Black could only move rooks and knights, and therefore he has made an even number of moves. This implies that White has made
Two gunshots were fired through the window of a coffee shop. When the police arrived, they successfully recognized which gunshot was fired first. Which was the first gunshot and how did they figure that out?

The cracks of the left gunshot end up right at the cracks of the right gunshot. Therefore the first gunshot is the one on the right.
Can you draw uncountable many non-intersecting “8” shapes in the plane (they can be contained in one another)?

No, you can’t. For each “8” shape you can choose a pair of points with rational coordinates – one in its top loop and one in its bottom loop. Since no two “8” shapes can have the same corresponding pair of rational points, their number should be countable.
A prince decides to get married to the prettiest girl in his kingdom. All 100 available ladies go to the palace and show themselves to the prince one by one. He can either decide to marry the girl in front of him or ask her to leave forever and call the next one in line. Can you find a strategy which will give the prince a chance of 25% to get married to the prettiest girl? Can you find the best strategy?
Remark: Assume that the prince can objectively compare every two girls he has seen.

A strategy which ensures a chance of 25% is the following:
The prince banishes the first 50 girls which enter the palace and then gets married to the first one which is prettier than all of them (if such one arrives). If the prettiest girl in the kingdom is in the second 50, and the second prettiest girl is in the first 50, he will succeed. The chance for this is exactly 25%.
The best strategy is to wait until ~1/e of all girls pass, and then choose the first one which is more beautiful than all of them. This yields a chance of ~37% for succeeding. The proof is coming soon.
Take six coins and arrange them in a triangle as shown in the image. Your goal is to rearrange the coins into a hexagon with only four moves. Every move consists of sliding one coin to a new location where it touches at least two other coins.

The solution is shown below.

A square has dropped on the ground and broken into ten pieces. Accidentally, an additional, eleventh piece has fallen among the others. Can you figure out which one it is?
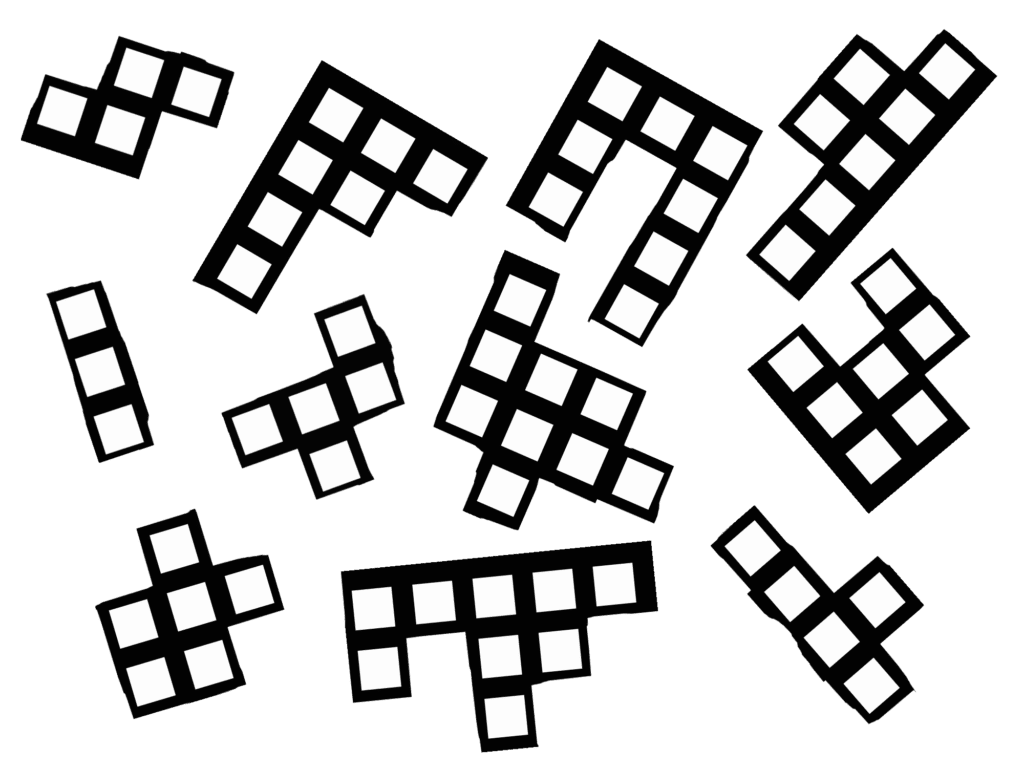
The total number of the squares in all pieces is 70 = 8 * 8 + 6. Therefore the extra piece is the one consisted of 6 squares.
Two people play a game of NIM. There are 100 matches on a table, and the players take turns picking 1 to 5 sticks at a time. The person who takes the last stick wins the game. Who has a winning strategy?
The first person has a winning strategy. First, he takes 4 sticks. Then every time the second player takes X sticks, the first player takes 6 – X sticks.
Two very short friends, John and Jack, were living together in an apartment. Since they used to lose their apartment key very often, they decided to leave it on top of the door frame when they leave home. In order to reach the key, John was climbing on Jack’s shoulders and thus taking it down from the frame. However, John was the taller and the heavier guy of the two. Why didn’t Jack climb on top of his shoulders instead?
The reason is that as being taller, John also had longer arms. If Jack climbed on John’s shoulders, he wouldn’t have reached the key.
Please confirm you want to block this member.
You will no longer be able to:
Please allow a few minutes for this process to complete.