In This Shoe…
Fill the three missing numbers (using words) in the shoe below.
Remark: The missing words can be of any length.
SOLUTION
You should fill the words FIVE, THREE, FOUR to get:
“In this shoe, there are five H’s, three O’s, and four T’s.”
Category: Brain Teasers
A collection of Math, Chess, Detective, Lateral, Insight, Science, Practical, and Deduction puzzles, carefully curated by Puzzle Prime.
We do not know where this puzzle originated from. If you have any information, please let us know via email.
Bicycle Tracks
You are chasing a criminal riding a bicycle, and you find his tracks left in the dirt. By investigating the tracks, can you determine which direction the criminal has fled to: left or right?
SOLUTION
The front wheels of the bicycle are traveling more distance and making sharper turns. Thus, the red tracks (as shown on the image below) correspond to the front wheel, and the green tracks correspond to the back wheel.
Then, since the back wheel is always pointing towards the front wheel, we conclude that the bicycle is moving towards the right.
STANDARD Word
Given the word STANDARD, take away two letters and then add three digits to make a logical sequence.
SOLUTION
Remove the two letters A to get ST-ND-RD and then add the digits 1, 2, 3 to get 1ST-2ND-3RD.
Toasting Bread
Your toaster is broken, so you decide to toast your bread in a pan. The pan can hold three slices of bread at a time and takes 1 minute to toast one of their sides. How much time would it take you to toast four slices of bread on both sides using the pan?
SOLUTION
It would take you 2 minutes and 40 seconds. Label the slices with A, B, C, D, their top sides A1, B1, C1, D1, and their bottom sides A2, B2, C2, D2.
- Toast A1, B1, C1 for 40 seconds.
- Toast A2, B2, D1 for 40 seconds.
- Toast A1, C2, D2 for 20 seconds.
- Toast A2, C2, D2 for 20 seconds.
- Toast B1, C1, D1 for 20 seconds.
- Toast B2, C2, D2 for 20 seconds.
100 Guests in 99 Rooms
One hundred people entered a hotel that had 99 rooms, and each of them asked for their own room. In order to solve the problem, the bellboy did the following:
He asked the 100th guest to wait for a while with the 1st guest in room number 1, so that there were 2 guests inside. Then he took the 3rd guest to room number 2, the 4th guest to room number 3, and so on, until finally taking the 99th guest to room number 98. At the end he returned to room number 1 and took the 100th guest to room number 99, which was still vacant.
How could everybody get their own room?
SOLUTION
The two people who were taken to room number 1 were guest 1 and guest 100. Thus, the 2nd guest ended up without a room.
Died on the Fourth of July
During a trivia night, the following question appeared:
“Among the first five US presidents, Washington, Adams, Jefferson, Madison, and Monroe, there were 3 who died on the fourth of July. Can you guess which ones?”
After nobody answered the question, the following hint was given:
“These three presidents were consecutive ones.”
Then, all contestants immediately managed to answer the question. Can you?
SOLUTION
Because of the way the question was worded, it was clear that the fifth president, James Monroe, was one of them. Otherwise, the trivia question would have been “among the first four US presidents” instead of “among the first five”. Since the three presidents that died on fourth of July were consecutive ones, they were Jefferson, Madison, and Monroe.
Limbs
Partition the grid into disjoint “creatures”, according to the following rules:
- Each creature is defined as a shape of 4 connected branches that are each 1 cell wide.
- For each creature, one of the branches ends up with a HEAD (always clued) and the other three branches end up with LIMBS (whenever clued, their directions matter).
- A creature can never occupy a 2×2 region of cells and can never touch itself.
Examine the first example, then solve the other three puzzles.
SOLUTION
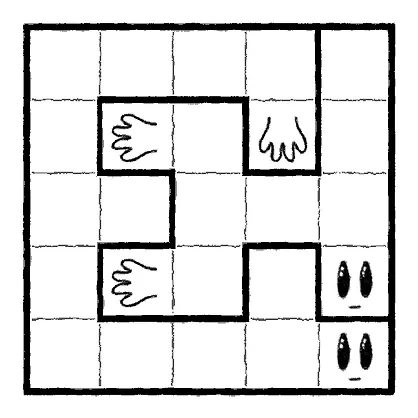
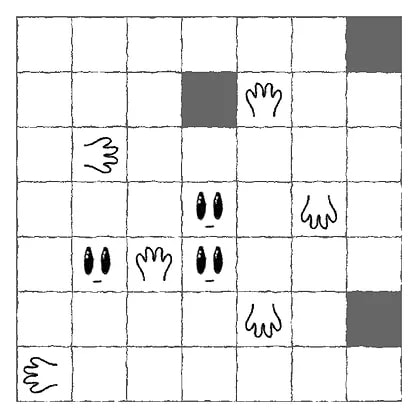
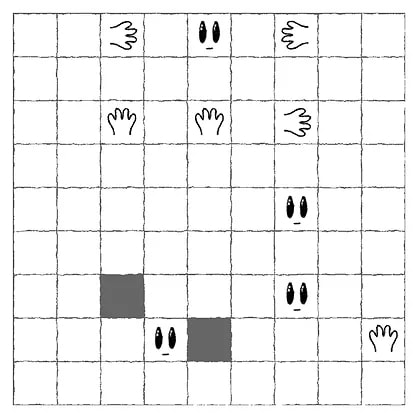
The solutions are shown below.
Do Not Add E
Add a single letter at the end to create a meaningful word. You CANNOT add the letter E.
S E Q U E N C _
SOLUTION
You should add the letter F above the underscore to create the letter E and get the word SEQEUNCE.
1 2 3 4 5 ?
Can you guess what the question mark should be replaced with? The answer is not 6.
| 1 | 3 | 5 |
| 2 | 4 | ? |
SOLUTION
The missing symbol is R, as in a car’s gears.
Mammals in Cages
You walk into a room where there are three mammals held in cages:
- a trained dog doing tricks
- a monkey playing with blocks
- a lab rat traversing a maze
Which is the most intelligent mammal in the room?
SOLUTION
The answer is… YOU.