Split the Cube
Can a cube be split into smaller cubes, all with different sizes?
SOLUTION
Solution coming soon.
Category: Puzzles
We do not know where this puzzle originated from. If you have any information, please let us know via email.
Panther Eyes
Find your way from one of the panther’s eyes to the other.
SOLUTION
Solution coming soon.
Airplane on a Conveyor Belt
A Boing 747 is sitting on a conveyor belt, as wide and long as a runway. The conveyor belt is designed to exactly match the speed of the wheels, moving in the opposite direction. Will the plane take off?
SOLUTION
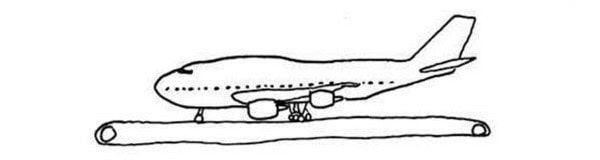
Solution coming soon.
Had Had Had Had Had
A teacher in English had asked James and John to describe a man who had suffered from a cold in the past. James while John had had had had had had had had had had had a better effect on the teacher.
Add punctuation to the sentence in bold, so that it makes sense.
SOLUTION
A teacher in English had asked James and John to describe a man who had suffered from a cold in the past. James, while John had had “had”, had had “had had”; “had had” had had a better effect on the teacher.
The meaning is that John had used the phrase “had a cold”, whereas James had used the phrase “had had a cold”. The former, being more grammatical, had resulted in a better impression on the teacher.
Fold Into a Cube
Cut out the black shape and then fold it perfectly into a cube, without overlapping.
SOLUTION
If the size of each of the small edges of the shape is equal to 1cm, then its area is equal to 30cm². Thus, the cube that is formed by the shape must have an edge of length √5cm. If we set the center of the black shape to be the center of one of the cube’s faces, then the four closest vertices must lie on the boundary of the shape, √2.5cm away. This determines uniquely the folding of the shape which is shown on the simulation below.
Source:
Average Salary
Three friends, A, B and C, want to find out what their average salary is without disclosing their own salaries to the others. How can they do it using only verbal communication?
SOLUTION
A tells B some number, then B adds his salary to it and tells the result to C, then C adds his salary and tells the result to A. Now A subtracts the number he told B in the beginning, adds his own salary and divides by 3. Repeat the same procedure with B and C starting first.
Help Mrs Vampire
Help
SOLUTION
The solution is shown below.
Eminent King
Five hundred begins it,
five hundred ends it,
five in the middle is seen.
The first of all letters,
the first of all numbers
take up their stations between.
Put them all together
and bring before you
the name of an eminent king.
SOLUTION
The answer is DAVID. In Roman numerals D=500, V=5, I=1.
Six Glasses
Six identical glasses are placed in a row on the table – first three filled with water, and then three empty ones. Can you move just one glass, so that empty and full glasses alternate?
SOLUTION
Take the second full glass, pour all the water into the second empty glass, and then put it back in its place.
Celebrity Names 3
What celebrity names do these cave paintings represent?
SOLUTION
The answers are:
- (Mice – Ice) + Eye + Yell + Fast + Bender = Michael Fassbender
- Dam + Sander = Adam Sandler
- Ant on a Knee + Hop + Kins = Anthony Hopkins
