11 is a Racehorse
Can you figure out what story the following sequence of statements is telling?
- 11 is a racehorse
- 12 is 12
- 1111 race
- 12112
11 is a racehorse. 12 is one (1) too (2). 11 won (1) one (1) race. 12 won (1) one (1) too (2).
We do not know where this puzzle originated from. If you have any information, please let us know via email.
Can you figure out what story the following sequence of statements is telling?
11 is a racehorse. 12 is one (1) too (2). 11 won (1) one (1) race. 12 won (1) one (1) too (2).
If you turn the handle of the top left gear clockwise, will the box in the bottom right open or close?
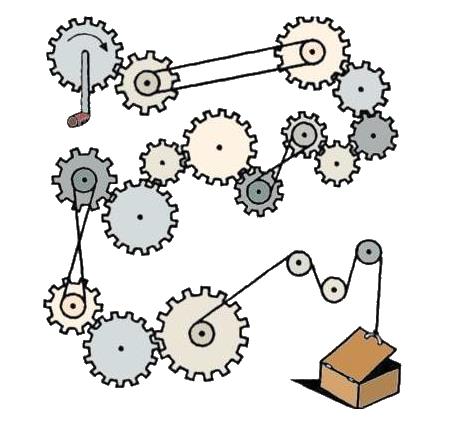
The box will open.
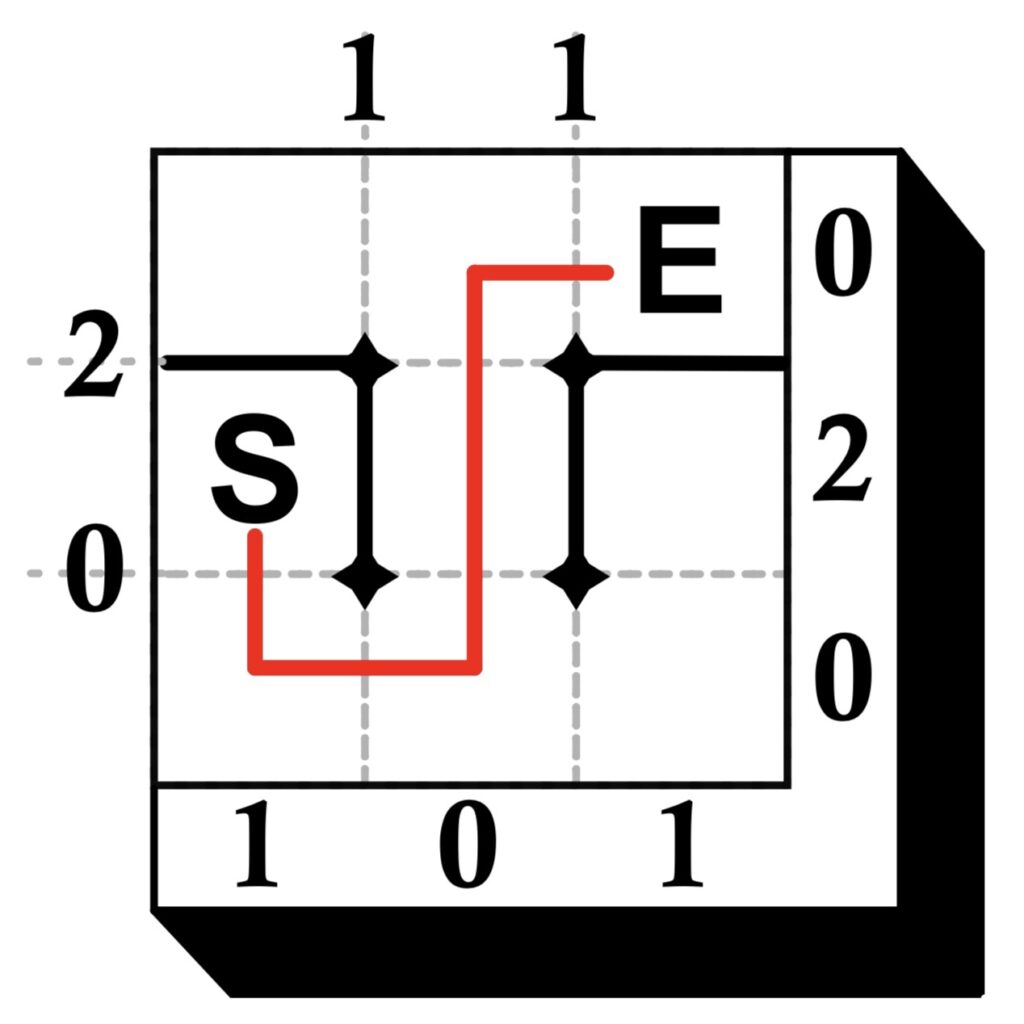
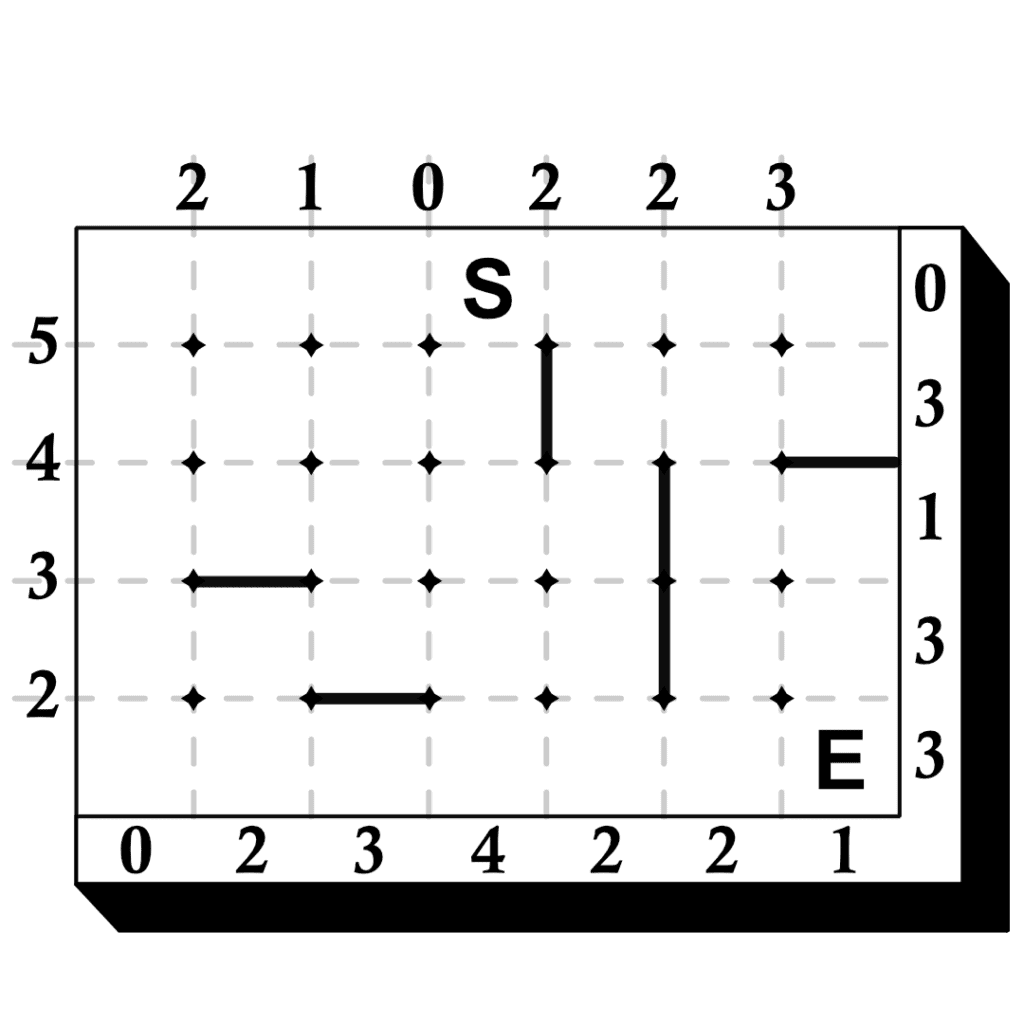
The main challenge of a Sunome puzzle is drawing a maze. Numbers surrounding the outside of the maze border give an indication of how the maze is to be constructed. To solve the puzzle you must draw all the walls where they belong and then draw a path from the Start square to the End square.
The walls of the maze are to be drawn on the dotted lines inside the border. A single wall exists either between 2 nodes or a node and the border. The numbers on the top and left of the border tell you how many walls exist on the corresponding lines inside the grid. The numbers on the right and bottom of the border tell you how many walls exist in the corresponding rows and columns. In addition, the following must be true:
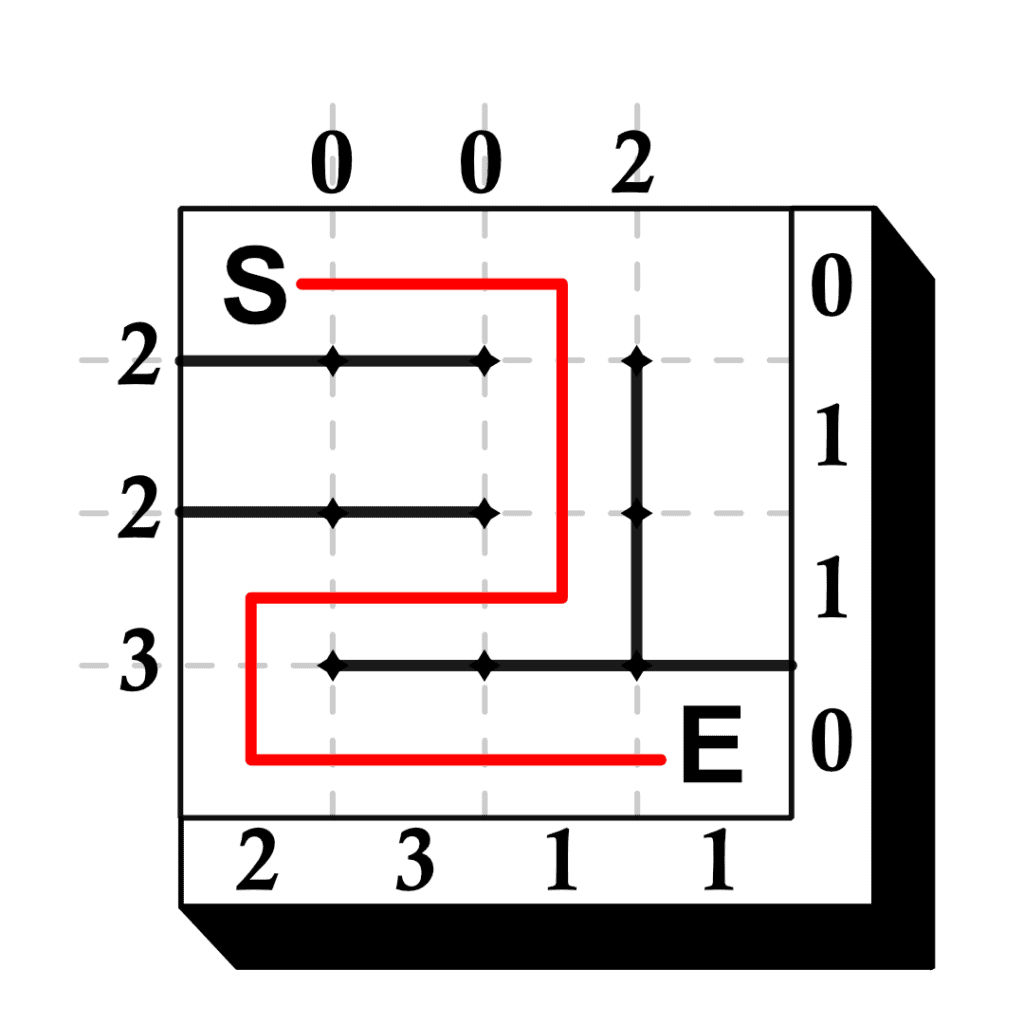
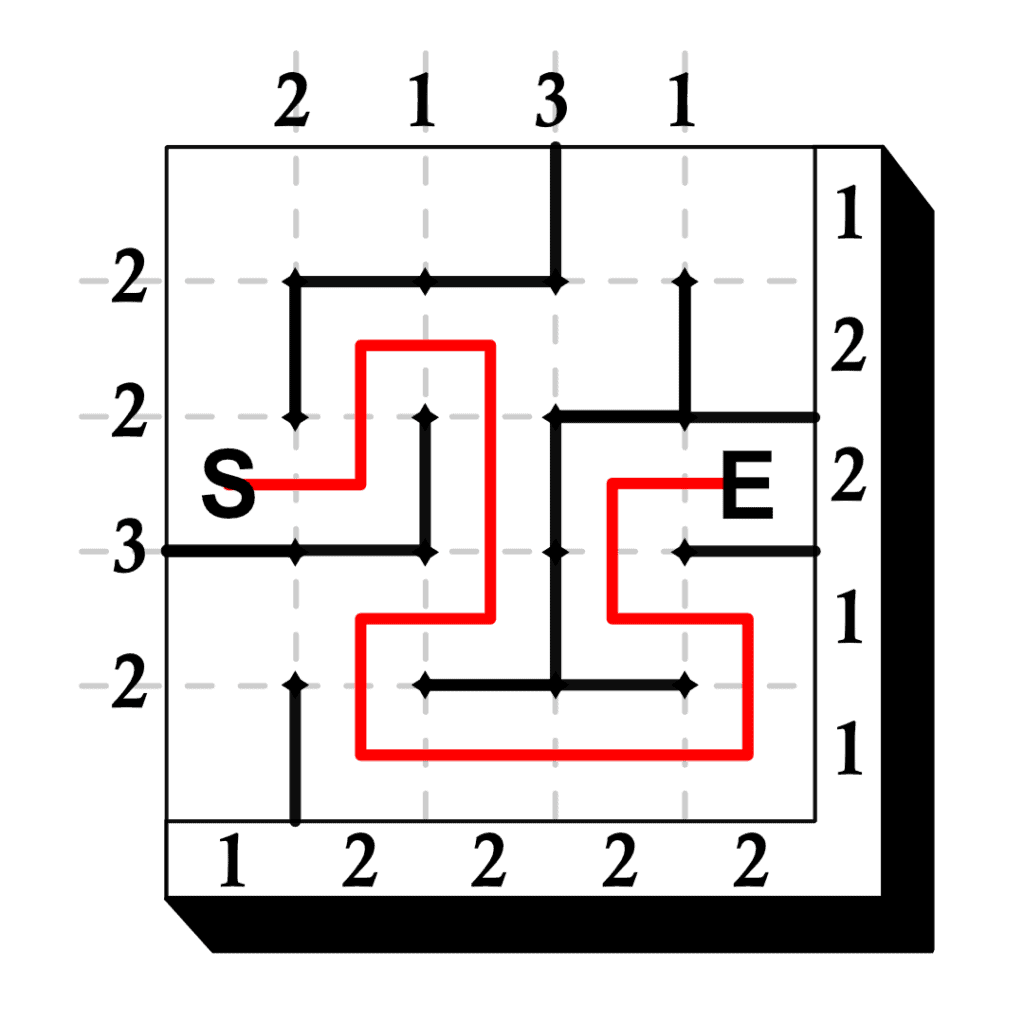
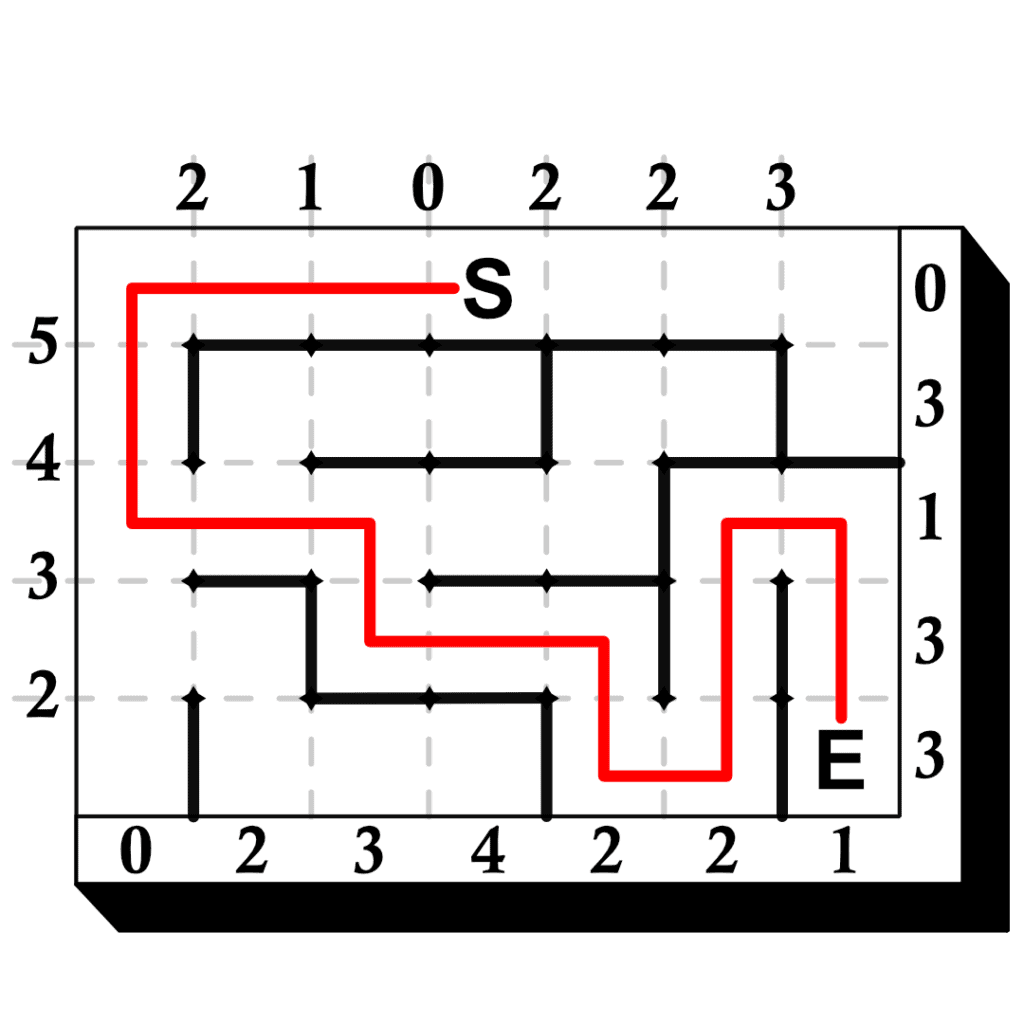
Examine the first example, then solve the other three puzzles.
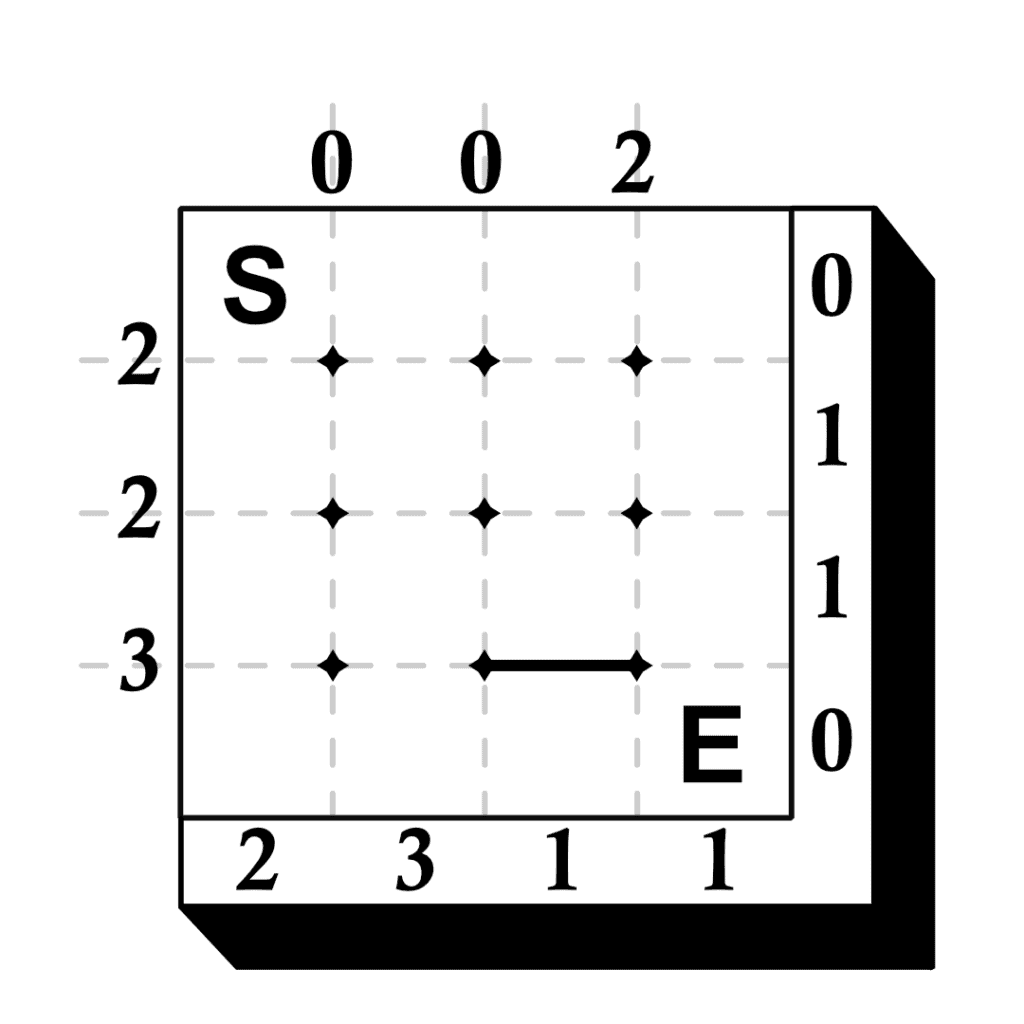
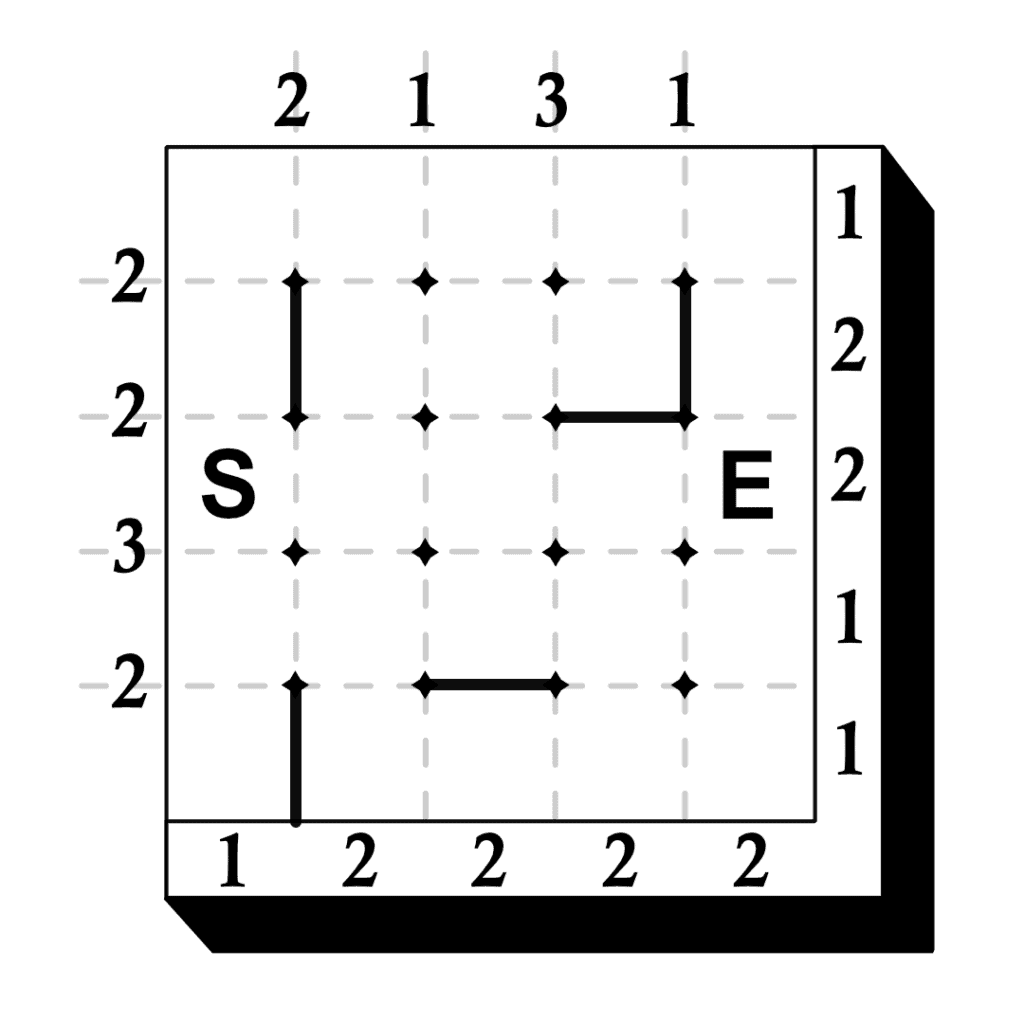
The solutions are shown below.
Separate all the goats from the cabbage in the picture by drawing 3 straight lines.
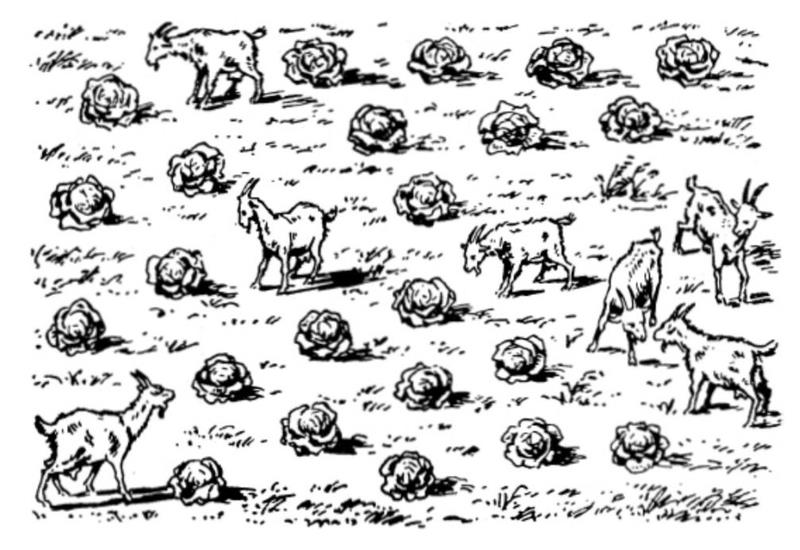
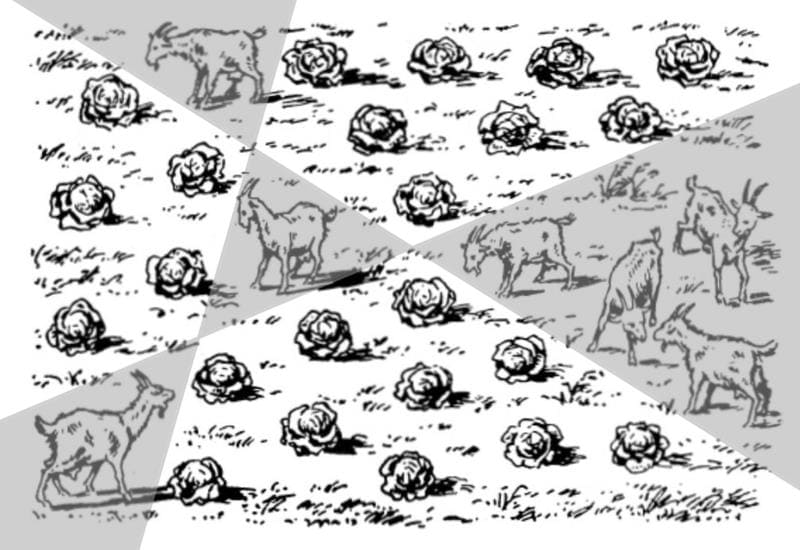
The solution is shown below.
Fill the three missing numbers (using words) in the shoe below.
Remark: The missing words can be of any length.

You should fill the words FIVE, THREE, FOUR to get:
“In this shoe, there are five H’s, three O’s, and four T’s.”
Your toaster is broken, so you decide to toast your bread in a pan. The pan can hold three slices of bread at a time and takes 1 minute to toast one of their sides. How much time would it take you to toast four slices of bread on both sides using the pan?
It would take you 2 minutes and 40 seconds. Label the slices with A, B, C, D, their top sides A1, B1, C1, D1, and their bottom sides A2, B2, C2, D2.
One hundred people entered a hotel that had 99 rooms, and each of them asked for their own room. In order to solve the problem, the bellboy did the following:
He asked the 100th guest to wait for a while with the 1st guest in room number 1, so that there were 2 guests inside. Then he took the 3rd guest to room number 2, the 4th guest to room number 3, and so on, until finally taking the 99th guest to room number 98. At the end he returned to room number 1 and took the 100th guest to room number 99, which was still vacant.
How could everybody get their own room?
The two people who were taken to room number 1 were guest 1 and guest 100. Thus, the 2nd guest ended up without a room.
During a trivia night, the following question appeared:
“Among the first five US presidents, Washington, Adams, Jefferson, Madison, and Monroe, there were 3 who died on the fourth of July. Can you guess which ones?”
After nobody answered the question, the following hint was given:
“These three presidents were consecutive ones.”
Then, all contestants immediately managed to answer the question. Can you?
Because of the way the question was worded, it was clear that the fifth president, James Monroe, was one of them. Otherwise, the trivia question would have been “among the first four US presidents” instead of “among the first five”. Since the three presidents that died on fourth of July were consecutive ones, they were Jefferson, Madison, and Monroe.
Please confirm you want to block this member.
You will no longer be able to:
Please note: This action will also remove this member from your connections and send a report to the site admin. Please allow a few minutes for this process to complete.