3 by 3
Can you draw a path consisting of 4 line segments which passes through all points in the grid?
SOLUTION
Yes, you can, as shown on the picture below.
Category: Insight
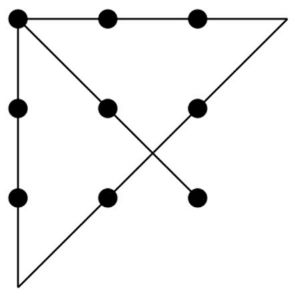
We do not know where this puzzle originated from. If you have any information, please let us know via email.
The White House
If Mr. Green lives in the green house and Mr. Red lives in the red house, who lives in the White House?
SOLUTION
The President.
$5 Bill
Bern tells Sandy, “This isn’t the $20 bill you left on the table. It is mine – I was keeping it between pages 15 and 16 of my textbook.”
Sandy retorts, “You are lying and I can prove it.” How does she know?
SOLUTION
Pages 15 and 16 are on the same sheet of paper in the textbook (just like pages 1 and 2 are) and therefore the bill couldn’t be between them.
FEATURED
Heads Up, Heads Down
You are blindfolded and on the table, in front of you, 50 coins are placed. You are told that X of them are heads up and the rest are heads down. Then you are asked to separate the coins into two groups and optionally flip some of them so that the number of heads in both groups becomes the same. How can you do this?
SOLUTION
Separate the coins into one group of X coins and into another group of 50-X coins, then flip every coin in the first group. If in the first group there were Y heads up initially, then after flipping there would be X-Y – exactly the number of heads up in the second group.
The Man in the Photo
A person is looking at somebody’s photo and exclaims:
“Brothers and sisters, I have none,
But this man’s father is my father’s son.”
Who is the person in the photo?
SOLUTION
It is the person’s son.
Mixed Up Pills
One patient has two bottles with 30 pills each and every night has to take one pill from each of the bottles. Unfortunately one night after he takes out a pill from the first bottle and places it on the table, by accident drops two pills from the second bottle right next to it. The pills look identical, so he can not differentiate them. It is very important that he continues his treatment diligently throughout the entire timespan of 30 days. What should the patient do?
SOLUTION
The patient should keep taking one pill from each bottle until there are 4 pills remaining – 1 in the first bottle and 3 on the table. On the 29th day he splits the pills in halves and takes one half from each pill. On the 30th day he takes the remaining halves of the pills.
Four Chains
You have four metal chains and each of them has three links. What is the minimal number of cuts you need to make so that you can connect the chains into one loop with twelve links?
SOLUTION
You need only three cuts – cut all the links of one of the chains and then use them to connect the ends of the remaining three chains.
The Number in the Yellow Circle
Which is the missing number in the yellow circle?
SOLUTION
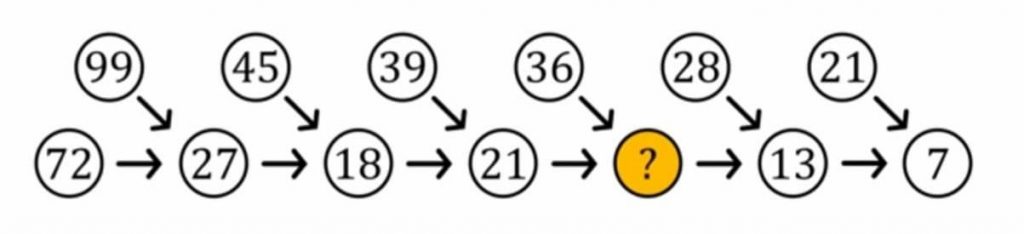
The missing number is 12. Each number is equal to the sum of the digits of the numbers pointing towards it.
A Good Bet
Someone tells you: “I’ll bet you $1 that if you give me $3, I will give you $5 in return”. Is this a good bet?
SOLUTION
You should not accept the bet and give him $3. If the person gives you the $5, then you would have given him $1+$3=$4, and you would make a profit of $1. However, the person can simply not give you anything and you will lose $3-$1=$2.
A Note in a Math Class
A boy receives a small note from a girl during his math class. He unfolds the note and sees the following expression.
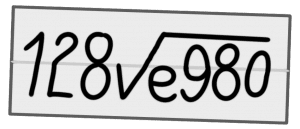
What does it mean?
SOLUTION
If you fold the note the other way around, the message “I LOVE YOU” appears.
