Mathematics 2 - Puzzle Prime

A String Around a Rod

Section: Brain Teasers Category: Mathematics

Difficulty: Medium Tags: Geometry

A string is wound around a circular rod with circumference 10 cm and length 30 cm. If the string goes around the rod exactly 4 times, what is its length?

SOLUTION

Imagine the circular rod is actually a paper roll and the string is embedded inside the paper. When we unroll it, we get a paper rectangle 30cm×40cm with the string embedded along the diagonal. Using the Pythagorean theorem, we find that the length of the string is 50cm.

Unknown Author October 7, 2023

0 Comments

FEATURED

Lost In the Forest

Section: Brain Teasers Category: Mathematics

Difficulty: Expert Tags: Featured, Geometry

You are lost in the middle of a forest, and you know there is a straight road exactly 1 km away from you, but not in which direction. Can you find a path of distance less than 640 m which will guarantee you to find the road?

SOLUTION

Imagine there is a circle with a radius of 100 m around you, and you are at its center O. Let the tangent to the circle directly ahead of you be t. Then, follow the path:

Turn left 30 degrees and keep walking until you reach the tangent t at point A for a total of 100×2√3/3 meters, which is less than 115.5 meters.
Turn left 120 degrees and keep walking along the tangent to the circle until you reach the circle at point B for a total of 100×√3/3 which is less than 58 meters.
Keep walking around the circle along an arc of 210 degrees until you reach point C for a total of 100×7π/6 which is less than 366.5 meters.
Keep walking straight for 100 meters until you reach point D on the tangent t.

Unknown Author September 22, 2023

3 Comments

An Ant’s Path

Section: Brain Teasers Category: Mathematics

Difficulty: Medium

An ant is positioned at one of the vertices of a cube and wants to get to the opposite vertex. If the edges of the die have length 1, what is the shortest distance the ant needs to travel?

SOLUTION

We unfold a cube to get a cross-shaped figure. Then, the problem is to find the shortest path between two points separated by a horizontal distance of 2 units and a vertical distance of 1 unit.

It is easy to see that the path in question is the one passing through the middle of the edge between the start and end points, and which has a distance of √5.

Unknown Author September 19, 2023

5 Comments

A Square and an Invisible Point

Section: Brain Teasers Category: Mathematics

Difficulty: Medium

There is a square drawn on a piece of paper and also a point marked with invisible ink. You are allowed to draw 3 lines on the paper and for each of them you will be told whether the point is on its left, on its right, or lies on the line. Your task is to find out whether the point is inside the square, outside the square, or on its boundary. How do you do it?

SOLUTION

Draw one of the diagonals of the square. Then, draw the 2 lines containing the sides of the square that are on the same side as the invisible point.

Unknown Author September 10, 2023

0 Comments

Toggle a Pixel

Section: Brain Teasers Category: Mathematics

Difficulty: Advanced

Toggle one pixel to make this equality correct.

SOLUTION

(71+1)×(71-1) = 7×6×…×2×1 = 7!

Unknown Author July 28, 2023

0 Comments

FEATURED

Eye of the Dragon

Section: Brain Teasers Category: Mathematics

Difficulty: Advanced Tags: Featured, Geometry

Divide the circle below in two pieces. Then, put the pieces together to get a circle with a dragon, such that the dragon’s eye is at the center of the new circle.

SOLUTION

The solution is shown below.

Unknown Author July 25, 2023

0 Comments

Cut the Pizza

Section: Brain Teasers Category: Mathematics

Difficulty: Hard Tags: Geometry

Cut a circular pizza into 12 congruent slices, such that exactly half of them contain crust.

Remark: We say that a slice contains crust if it shares an arc with the boundary of the pizza (with non-zero measure).

SOLUTION

First, cut the pizza into 6 congruent circular triangles, and then split each of them in half, as shown on the image below.

Unknown Author July 13, 2023

4 Comments

Missing Parenthesis

Section: Brain Teasers Category: Mathematics

Difficulty: Advanced

Insert the missing parentheses into each equation to make it true.

SOLUTION

The solutions are:

(((9+12)÷(3+4))÷(2+1))×2 = 2
((9+12)÷3)+4÷(2+1×2) = 8
(9+12)÷3+4÷2+1×2 = 11
9+12÷(3+4÷(2+1×2))= 12

Source:

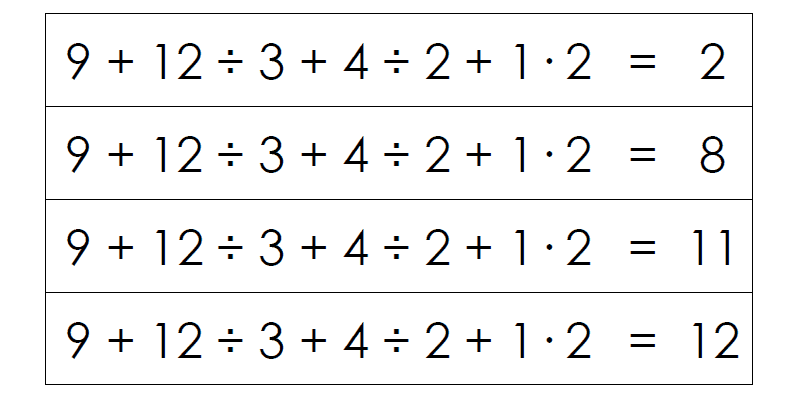
“Intermediate Algebra for College Students” by Karl. J. Smith and Patrick J. Boyle

Karl Smith and Patrick Boyle June 28, 2023

2 Comments

Spot the Robber

Section: Brain Teasers Category: Mathematics

Difficulty: Hard

The streets of the city are a square grid that extends infinitely in all directions. One of the streets has a police officer stationed every 100 blocks and there is a robber is somewhere in the city.

Can you devise a strategy that guarantees the robber will be spotted by a police officer at some point, no matter how he tries to avoid them?

Note: The officers can see infinitely far, but their running speeds are lower than the speed of the robber.

SOLUTION

Let the police officers are located at points with coordinates (100N, 0) for N = 0, ±1, ±2… First, we fix the positions of all officers stationed at points (±200N, 0), then repeatedly perform the following procedure, step by step:

On step M, we let the non-fixed officers who are closest to the center move to the free points with coordinates (K, 0) and (0, K) for K = 0, ±1, ±2, … ±M. Then we fix their positions.

Since there are fixed officers at points (200N, 0) at all times, the robber is contained within some vertical strip the entire time. Therefore, at some point there will be two fixed officers that will restrict the robber within a horizontal segment of size 1, at coordinates (x, T) for x ∈ (S, S+1) and some T. Finally, at some point an officer will move to the point (0, T) and will spot the robber.

Alex Lvovsky June 13, 2023

0 Comments

Numbers on a Dodecahedron

Section: Brain Teasers Category: Mathematics

Difficulty: Advanced

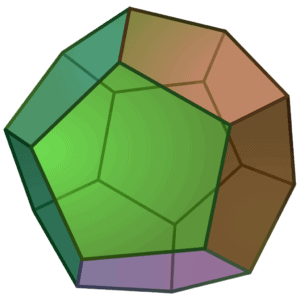
We have written the numbers from 1 to 12 on the faces of a regular dodecahedron. Then, we have written on each vertex the sum of the five numbers on the faces incident with it. Is it possible that 16 of these 20 sums are the same?

SOLUTION

We color the vertices in five colors as shown in the image below, such that each face of the dodecahedron has 1 vertex of each color. Then, the sum of the four numbers from each color must be equal to the sum of all numbers written on the faces: 1 + 2 + … + 12 = 78.

If 16 of the vertices have the same number written on them, then by the pigeonhole principle there will be 4 vertices with identical colors and identical numbers. Since 78 is not divisible by 4, we conclude that this is impossible.

Unknown Author April 13, 2023

0 Comments