Mathematics 6 - Puzzle Prime

Fish in a Pond

Section: Brain Teasers Category: Mathematics

Difficulty: Expert Tags: Probability

There are 5 fish in a pond. What is the probability that you can split the pond into 2 halves using a diameter, so that all fish end up in one half?

SOLUTION

Let us generalize the problem to N fish in a pond. We can assume that all fish are on the boundary of the pond, which is a circle, and we need to find the probability that all of them are contained within a semi-circle.

For every fish Fᵢ, consider the semi-circle Cᵢ whose left end-point is at Fᵢ. The probability that all fish belong to Cᵢ is equal to 1/2ᴺ⁻¹. Since it is impossible to have 2 fish Fᵢ and Fⱼ, such that the semi-sircles Cᵢ and Cⱼ contain all fish, we see that the probability that all fish belong to Cᵢ for some i is equal to N/2ᴺ⁻¹.

When N = 5, we get that the answer is 5/16.

Unknown Author August 10, 2021

3 Comments

Rapunzel and the Prince

Section: Brain Teasers Category: Mathematics

Difficulty: Medium Tags: Geometry

The evil witch has left Rapunzel and the prince in the center of a completely dark, large, square prison room. The room is guarded by four silent monsters in each of its corners. Rapunzel and the prince need to reach the only escape door located in the center of one of the walls, without getting near the foul beasts. How can they do this, considering they can not see anything and do not know in which direction to go?

SOLUTION

The prince must stay in the center of the room and hold Rapunzel’s hair, gradually releasing it. Then, Rapunzel must walk in circles around the prince, until she gets to the walls and finds the escape door.

Puzzle Prime August 1, 2021

2 Comments

Hungry Lion

Section: Brain Teasers Category: Mathematics

Difficulty: Expert

A hungry lion runs inside a circus arena which is a circle of radius 10 meters. Running in broken lines (i.e. along a piecewise linear trajectory), the lion covers 30 kilometers. Prove that the sum of all turning angles is at least 2998 radians.

SOLUTION

Imagine the lion is static, facing North, and instead, the center of the arena moves around. Then, each time the lion runs X meters in some direction, this translates into the center moving X meters South. Each time the lion makes a turn of Y radians, this translates into the center moving along an arc of Y radians.

Thus, the problem translates to a point inside the arena alternating between traveling straight South and then moving along arcs around the center of the arena. Since the total distance traveled straight South by the point is 30KM and the distance between the starting and the ending points is at most 20M, the total distance traveled North must be at least 30KM – 20M = 29980M. Therefore, the total length of the arcs traversed by the point is at least 29980M, and since the radius of each arc is at most 10M, the total angle of the arcs must be at least 2998 radians. The sum of all turning angles of the lion is the same, so this concludes the proof.

Unknown Author July 10, 2021

2 Comments

FEATURED

Houses on a Farm

Section: Brain Teasers Category: Mathematics

Difficulty: Hard Tags: Featured, Graph Theory

Is it possible to connect each of the houses with the well, the barn, and the mill, so that no two connections intersect each other?

SOLUTION

No, it is impossible. Here is a convincing, albeit a informal proof.

Imagine the problem is solvable. Then you can connect House A to the Well, then the Well to House B, then House B to the Barn, then the Barn to House C, then House C to the Mill, and finally the Mill to House A. Thus, you will create one loop with 6 points on it, such that houses and non-houses are alternating along the loop. Now, you must connect Point 1 with Point 4, Point 2 with Point 5, Point 3 with Point 6, such that the three curves do not intersect each other. However, you can see that you can draw no more than one such curve neither on the inside, nor the outside of the loop. Therefore, the task is indeed impossible.

More rigorous, mathematical proof can be made using Euler’s formula for planar graphs. We have that F + V – E = 2, where F is the number of faces, V is the number of vertices, and E is the number of edges in the planar graph. We have V = 6 and E = 9, and therefore F = 5. Since no 2 houses or 2 non-houses can be connected with each other, every face in this graph must have at least 4 sides (edges). Therefore, the total number of sides of all faces must be at least 20. However, this is impossible, since every edge is counted twice as a side and 20/2 > 9.

Unknown Author July 1, 2021

1 Comment

FEATURED

Game of Coins

Section: Brain Teasers Category: Mathematics

Difficulty: Hard Tags: Featured

Kuku and Pipi decide to play a game. They arrange 50 coins in a line on the table, with various nominations. Then, alternating, each player takes on their turn one of the two coins at the ends of the line and keeps it. Kuku and Pipi continue doing this, until after the 50th move all coins are taken. Prove that whoever starts first can always collect coins with at least as much value as their opponent.

Remark: On the first turn, Kuku can pick either coin #1 or coin #50. If Kuku picks coin #1, then Pipi can pick on her turn either coin #2 or coin #50. If Kuku picks coin #50, then Pipi can pick on her turn either coin #1 or coin #49.

SOLUTION

Let’s assume Kuku starts first. In the beginning, he calculates the total value of the coins placed on odd positions in the line and compares it with the total value of the coins placed on even positions in the line. If the former has a bigger total value, then on every turn he takes the end coin which was placed on odd position initially. If the latter has bigger value, then on every turn he takes the end coin which was placed on even position initially. It is easy to see that he can always do this because after each of Pipi’s turns there will be one “odd” coin and one “even” coin at the ends of the line.

Unknown Author June 28, 2021

2 Comments

Monochrome Isosceles Triangle

Section: Brain Teasers Category: Mathematics

Difficulty: Advanced

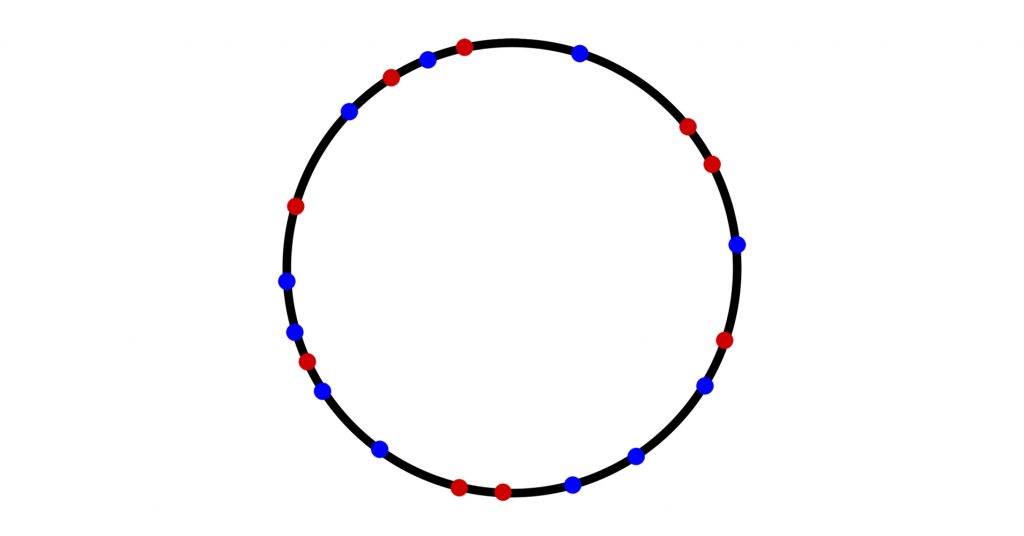
All points on a circle are colored in blue and red colors. Show that you can inscribe inside the circle an isosceles triangle whose vertices have the same color.

SOLUTION

Inscribe a regular pentagon inside the circle. Three of its five vertices must have the same color, and they form an isosceles triangle.

Unknown Author May 16, 2021

0 Comments

FEATURED

10 Dots, 10 Coins

Section: Brain Teasers Category: Mathematics

Difficulty: Expert Tags: Featured

If you have 10 dots on the ground, can you always cover them with 10 pennies without the coins overlapping?

SOLUTION

Assume the dots lie in a plane and the radius of a penny is 1. Make an infinite grid of circles with radii 1, as shown on the picture, and place it randomly in the plane.

If we choose any point in the plane, the probability that it will end up inside some circle of the grid is equal to S(C)/S(H), where S(C) is the area of a coin and S(H) is the area of a regular hexagon circumscribed around it. A simple calculation shows that this ratio is larger than 90%. Therefore, the probability that some chosen point in the plane will not end up inside any circle is less than 10%. If we have 10 points, the probability that neither of them will end up inside a circle is less than 100%. Therefore, we can place the grid in the plane in such a way that every dot ends up in some circle. Now, just place the given coins where these circles are.

Source:

The Mathematical Intelligencer, 34:3 [September 2012], 11-14

Naoki Inaba April 10, 2021

2 Comments

Coins on a Chessboard

Section: Brain Teasers Category: Mathematics

Difficulty: Hard

There is a room with a chessboard inside. On each of its 64 squares, there is placed a coin, either heads up or heads down. You enter the room and a person inside points towards one special square on the chessboard and gives you the chance to flip one of the coins (whichever you choose). Then you leave the room, your friend enters and has to guess which was the special square on the chessboard. If you two could devise a plan before entering the room, how would you make sure your friend always guesses correctly which is the special square?

SOLUTION

First, you must enumerate the coins with numbers from 1 to 64, locate the mystery coin, and calculate the binary representation of its number, padded with zeros on the left to 6 digits length. For example, if the mystery coin is the 5th one on the 4th row, its number would be 29 and will have a binary representation 011101. Then, consider the following sets of coins:

A1 = {row 1, row 2, row 3, row 4}
A2 = {row 1, row 2, row 5, row 6}
A3 = {row 1, row 3, row 5, row 7}
A4 = {column 1, column 2, column 3, column 4}
A5 = {column 1, column 2, column 5, column 6}
A6 = {column 1, column 3, column 5, column 7}

Now, the strategy is to flip the coin which makes the parity of heads in set Ai odd if and only if the i-th digit in the binary representation of the mystery coin is 1. It is easy to check that this is always a possible thing to do.

Unknown Author February 27, 2021

4 Comments

The Majority Name

Section: Brain Teasers Category: Mathematics

Difficulty: Hard Tags: Algorithm

In a long list of names, one of the names appears more than half of the time. You will be read the names one at a time, without knowing how many they are, and without being able to write them down. If you have a very weak memory, how can you figure out which is the majority name?

SOLUTION

Remember the first name and then keep track of whether it has been repeated more than half of the time. To do that, simply add 1 if you hear the name or subtract one when you hear another name. If the list finishes and your counter is positive, then the first name is the majority. If your counter drops to 0, simply restart the procedure with the next name you hear.

This algorithm, invented by R. Boyer and J. Moore, works, because if the counter ends up at 0, then each of the names up to that moment has been read at most half of the time. Therefore, the majority name appears more than half of the time in the remainder of the list.

Unknown Author February 6, 2021

1 Comment

Ambiguous Clock

Section: Brain Teasers Category: Mathematics

Difficulty: Hard

The hands of my alarm clock are indistinguishable. How many times throughout the day their positioning is such that one cannot figure out which is the hour hand, and which is the minute hand?

Remark: AM-PM is not important.

SOLUTION

Imagine that you have a third hand which moves 12 times as fast as the minute hand. Then, at any time, if the hour hand moves to the location of the minute hand, the minute hand will move to the location of the imaginary hand. Therefore, our task is to find the number of times during the day when the hour hand and the imaginary hand are on top of each other, and the minute hand is not.

Since the imaginary hand moves 144 times faster than the hour hand, the two hands are on top of each other exactly 143 times between 12AM and 12PM. Out of these 143 times, 11 times all three arrows are on top of each other. Therefore, we have 2 × (143 – 11) = 264 times when we cannot figure out the exact time during the entire 24-hour cycle.

Unknown Author January 27, 2021

1 Comment