Mathematics 8 - Puzzle Prime

The Pasta Puzzle

Section: Brain Teasers Category: Mathematics

Difficulty: Medium

You have 10 strings of pasta left on your plate. You randomly start tying up their ends, until there are no loose ends anymore. What is the average number of loops which are created?

SOLUTION

The expected (average) number of loops at the end of the procedure is equal to the expected number of loops created after the first tying, plus the expected number of loops created after the second tying, etc. After each tying, the number of non-loop strings decreases by 1, and then the probabilities to create a new loop are 1/19, 1/17, 1/15, etc. Therefore, the answer is the sum 1/19 + 1/17 + 1/15 + … + 1/3 + 1/1 ~ 2.1.

Unknown Author May 31, 2020

0 Comments

The Missing Digit

Section: Brain Teasers Category: Mathematics

Difficulty: Medium

The number 2²⁹ has 9 digits, all different. Which digit is missing?

Bonus: Is the number 9991 prime?

SOLUTION

Let the missing digit be m. Every number and the sum of its digits give the same remainder when divided by 9. The number 2²⁹ = 32 * 64⁴ gives remainder 5 when divided by 9, and therefore 9 divides (0 + 1 + 2 + … + 9) – 5 – m = 40 – m. Thus, the missing digit is 4.

Bonus: 9991 = 10000 – 9 = 100² – 32 = (100 – 3)(100 + 3) = 97 * 103. Therefore the number 9991 is not prime.

Unknown Author April 18, 2020

0 Comments

Cover the Table

Section: Brain Teasers Category: Mathematics

Difficulty: Hard

100 coins are placed on a rectangular table, such that no more coins can be added without overlapping. Show that you can cover the entire table with 400 coins (overlapping allowed).

SOLUTION

Since we can not place any more coins on the table, each point of it is at distance at most 2r from the center of some coin, where r is the radius of the coin. Now shrink the entire table twice in width and length, then replace every shrunk coin with a full sized one. This way the small table will be completely covered because every point of it will be at distance at most r from the center of some coin. Add three more of these smaller tables, covered with coins, to create a covering of the big table.

Unknown Author April 12, 2020

0 Comments

Borromean Rings

Section: Brain Teasers Category: Mathematics

Difficulty: Hard Tags: Geometry

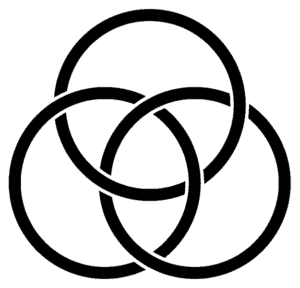
Borromean rings are rings in the 3-dimensional space, linked in such a way that if you cut any of the three rings, all of them will be unlinked (see the image below). Show that rigid circular Borromean rings cannot exist.

SOLUTION

Assume the opposite. Imagine the rings have zero thickness and reposition them in such a way, that two of them, say ring 1 and ring 2, touch each other in two points. These two rings lie either on a sphere or a plane which ring 3 must intersect in four points. However, this is impossible.

Unknown Author April 9, 2020

0 Comments

Seven Sevens

Section: Brain Teasers Category: Mathematics

Difficulty: Advanced Tags: Cryptarithm

Seven sevens are given. Find the other digits in this multiplication.

SOLUTION

The answer is:

21817 x 96787 = 2111601979

Leonid Mochalov March 31, 2020

2 Comments

Securing the Box

Section: Brain Teasers Category: Mathematics

Difficulty: Hard

There are 5 people who possess a box. You are allowed to secure the box with as many different locks as you like and distribute any combination of keys for these locks to any people among the 5. Find the least number of locks needed, so that no 2 people can open the box, but any cannot people can open it.

SOLUTION

For every subset of 2 people you pick among the 5, there should be a lock which none of the 2 can unlock, and each of the remaining 3 people can unlock. Clearly, the lock in question cannot be the same for any two different subsets of 2 people you choose. Therefore the number of locks you need is at least the number of different 2-element subsets of a 5-element set, which is 5!/(2!3!)=10. This number is sufficient as well – just give keys to a different group of 3 people for every lock.

Unknown Author February 1, 2020

0 Comments

Relabeling Dices

Section: Brain Teasers Category: Mathematics

Difficulty: Hard

Can you relabel two 6-sided dices, so that every face has a positive number of dots, and also their sum has the same probability distribution?

SOLUTION

Yes, you can do this. The easiest way is to use generating functions. Using simple polynomial algebra, you can see that

(x + x₂ + x₃ + x₄ + x₅ + x₆)² = (x + 2x₂ + 2x₃ + x₄)(x + x₃ + x₄ + x₅ + x₆ + x₈).

Therefore, if you take a dice with spots {1, 2, 2, 3, 3, 4}, and a dice with spots {1, 3, 4, 5, 6, 8}, their sum will have the same probability distribution.

Unknown Author January 28, 2020

0 Comments

The Lion and the Zebras

Section: Brain Teasers Category: Mathematics

Difficulty: Hard

The lion plays a deadly game against a group of 100 zebras that takes place in the steppe (an infinite plane). The lion starts in the origin with coordinates (0,0), while the 100 zebras may arbitrarily pick their 100 starting positions. The lion and the group of zebras move alternately:

In a lion move, the lion moves from its current position to a position at most 100 meters away.
In a zebra move, one of the 100 zebras moves from its current position to a position at most 100 meters away.
The lion wins the game as soon as he manages to catch one of the zebras.

Will the lion always win the game after a finite number of moves? Or is there a strategy for the zebras that lets them survive forever?

SOLUTION

The zebras can survive forever. They choose 100 parallel strips with width 300m each, then start on points on their mid-lines. If the lion lands on some zebra’s strip, the zebra simply jumps 100m away from the lion, along its mid-line.

Source:

Puzzling StackExchange

Gamow January 25, 2020

0 Comments

Square Cake

Section: Brain Teasers Category: Mathematics

Difficulty: Medium Tags: Geometry

There is a square cake at a birthday party attended by a dozen people. How can the cake be cut into twelve pieces, so that every person gets the same amount of cake, and also the same amount of frosting?

Remark: The decoration of the cake is put aside, nobody eats it.

SOLUTION

Divide the boundary of the cake into twelve equal parts, then simply make cuts passing through the separation points and the center. This way all tops and bottoms of the formed pieces will have equal areas, and also all their sides will have equal areas. Since all pieces have the same height, their volumes will be equal as well.

Unknown Author January 10, 2020

0 Comments

Wobbling Table

Section: Brain Teasers Category: Mathematics

Difficulty: Hard

A perfectly symmetrical square 4-legged table is standing in a room with a continuous but uneven floor. Is it always possible to position the table in such a way that it doesn’t wobble, i.e. all four legs are touching the floor?

SOLUTION

The answer is yes. Let the feet of the table clockwise are labeled with 1, 2, 3, 4 clockwise. Place the table in the room such that 3 of its feet – say 1, 2, 3, touch the ground. If foot 4 is on the ground, then the problem is solved. Otherwise, it is easy to see that we can not put it there if we keep legs 2 and 3 in the same places. Now start rotating the table clockwise, keeping feet 1, 2 and 3 on the ground at all times. If at some point foot 4 touches the ground as well, the problem is solved. Otherwise, continue rotating until foot 1 goes to the place where foot 2 was and foot 2 goes to the place where foot 3 was. Foot 3 will be on the ground, but this contradicts the observation that initially we couldn’t place legs 2, 3 and 4 on the ground without replacing feet 2 and 3.

Unknown Author December 25, 2019

0 Comments