A collection of Math, Chess, Detective, Lateral, Insight, Science, Practical, and Deduction puzzles, carefully curated by Puzzle Prime.
We do not know where this puzzle originated from. If you have any information, please let us know via email.
Cut a circular pizza into 12 congruent slices, such that exactly half of them contain crust.
Remark: We say that a slice contains crust if it shares an arc with the boundary of the pizza (with non-zero measure).
First, cut the pizza into 6 congruent circular triangles, and then split each of them in half, as shown on the image below.
White to play. Is this game a win for White, Black, or a draw?
This game is a win for White.
1. c7 Rd6+
2. Kb5 Rd5+
3. Kb4 Rd4+
4. Kb3 Rd3+
5. Kc2! Rd4!
6. c8=R! Ra4
7. Kb3
Now Black will either lose the rook, or get mated in one. If White promoted a Queen instead of a Rook, then 6… Rc4+ would lead to 7. Qxc4, which is a stalemate.
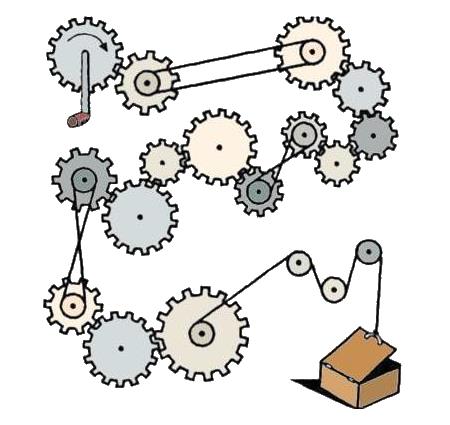
If you turn the handle of the top left gear clockwise, will the box in the bottom right open or close?
The box will open.
Insert the missing parentheses into each equation to make it true.
The solutions are:
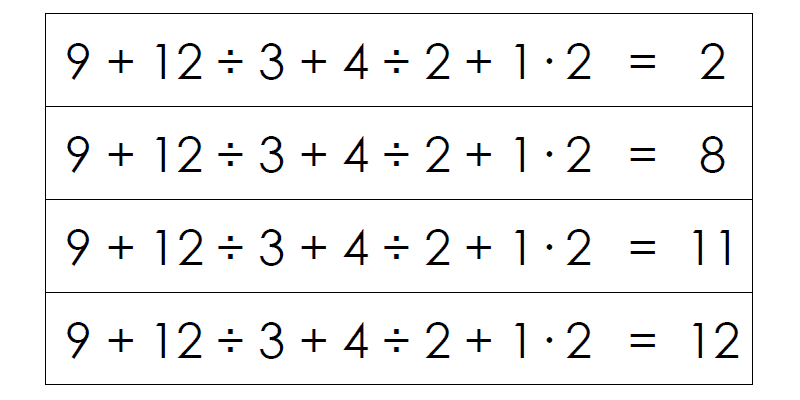
“Intermediate Algebra for College Students” by Karl. J. Smith and Patrick J. Boyle
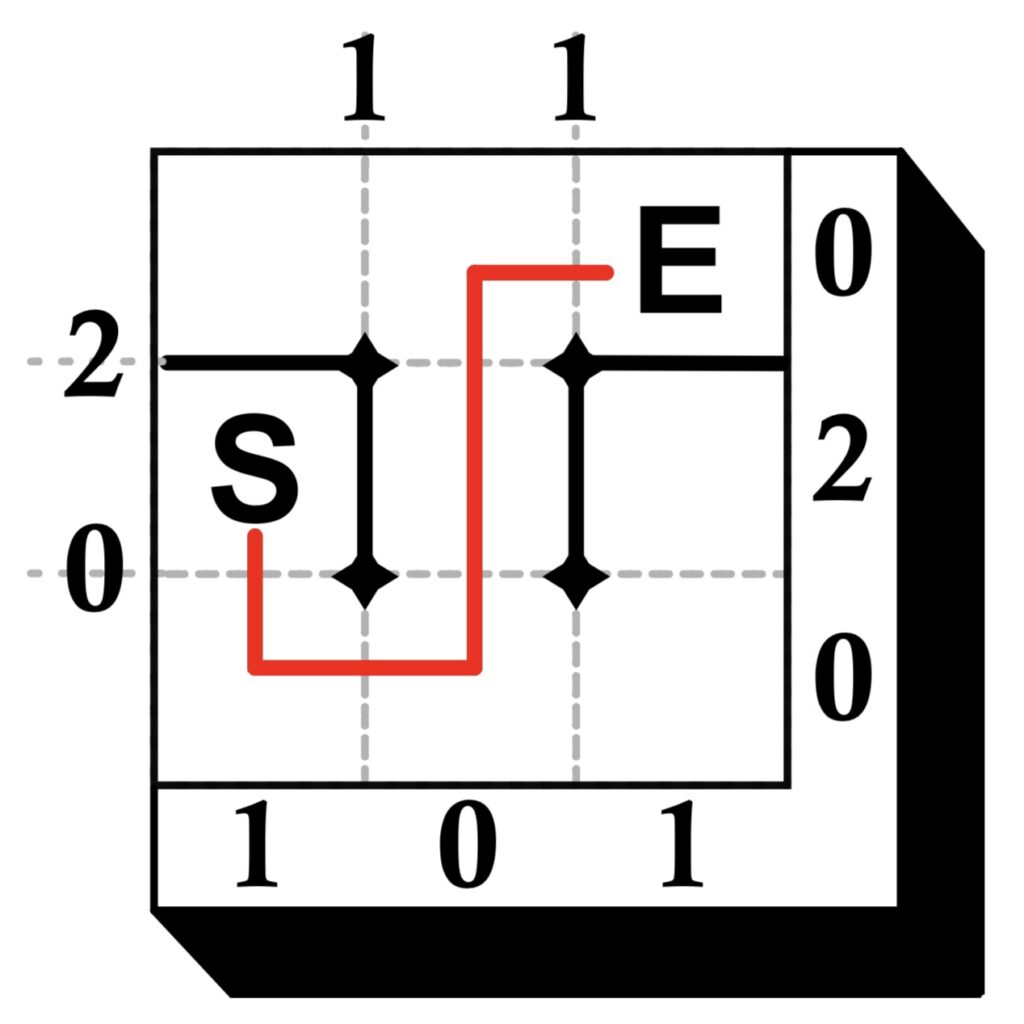
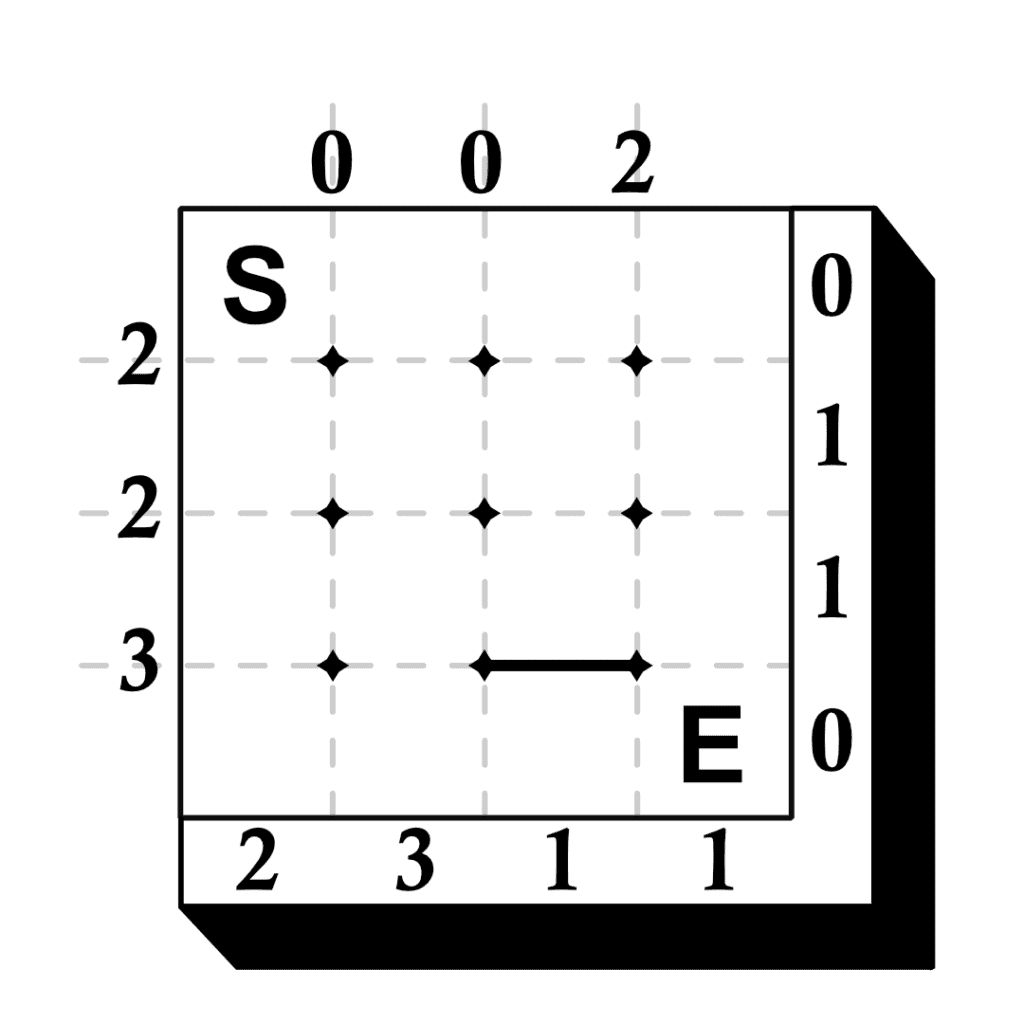
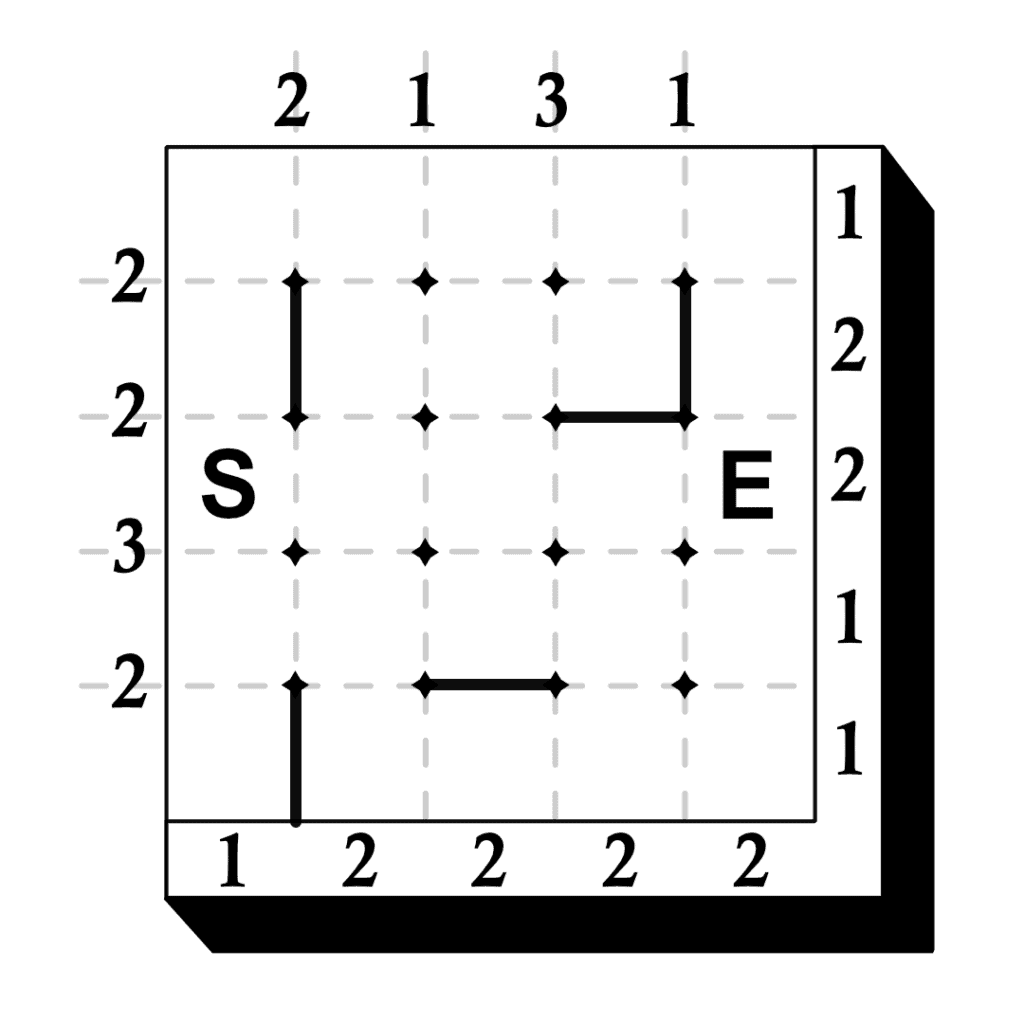
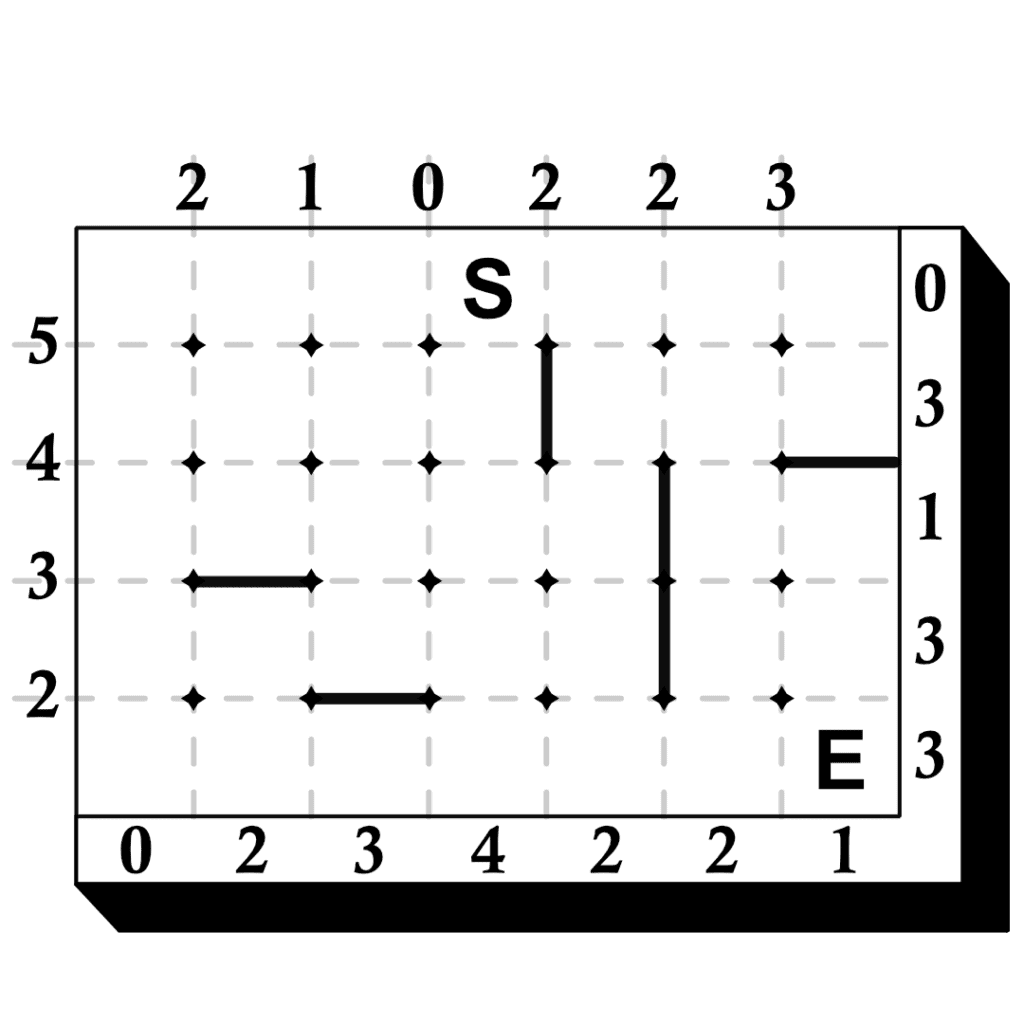
The main challenge of a Sunome puzzle is drawing a maze. Numbers surrounding the outside of the maze border give an indication of how the maze is to be constructed. To solve the puzzle you must draw all the walls where they belong and then draw a path from the Start square to the End square.
The walls of the maze are to be drawn on the dotted lines inside the border. A single wall exists either between 2 nodes or a node and the border. The numbers on the top and left of the border tell you how many walls exist on the corresponding lines inside the grid. The numbers on the right and bottom of the border tell you how many walls exist in the corresponding rows and columns. In addition, the following must be true:
Examine the first example, then solve the other three puzzles.
The solutions are shown below.
One day, the police finds a dead man inside a hut, with a bullet in his head. In his left hand, the man is holding a gun. In his right hand, he has a recording. When the recording is played, the police hears the man talking about how horrible his life has been and how he wanted it to end. The recording ends with a gunshot. The police are about to call it a suicide until a detective points out an important clue. What is it?
If the person shot himself and died, he wouldn’t have been able to stop the device from recording further.
The streets of the city are a square grid that extends infinitely in all directions. One of the streets has a police officer stationed every 100 blocks and there is a robber is somewhere in the city.
Can you devise a strategy that guarantees the robber will be spotted by a police officer at some point, no matter how he tries to avoid them?
Note: The officers can see infinitely far, but their running speeds are lower than the speed of the robber.
Let the police officers are located at points with coordinates (100N, 0) for N = 0, ±1, ±2… First, we fix the positions of all officers stationed at points (±200N, 0), then repeatedly perform the following procedure, step by step:
On step M, we let the non-fixed officers who are closest to the center move to the free points with coordinates (K, 0) and (0, K) for K = 0, ±1, ±2, … ±M. Then we fix their positions.
Since there are fixed officers at points (200N, 0) at all times, the robber is contained within some vertical strip the entire time. Therefore, at some point there will be two fixed officers that will restrict the robber within a horizontal segment of size 1, at coordinates (x, T) for x ∈ (S, S+1) and some T. Finally, at some point an officer will move to the point (0, T) and will spot the robber.
A very rich man has many servants in his mansion. One day as he is about to travel, his night watchman warns him not to board his flight. “I had a dream last night that the plane crashed,” the watchman tells him. The rich man is annoyed at first, but since he is also superstitious himself, he decides not to take the flight.
Later that day as he is watching the news, he sees that his plane did, in fact, crash. He goes over to thank and reward his servant, and then fires him. Why?
The watchman has been sleeping at work instead of guarding the mansion, so that’s the reason he gets fired.
Move the minus sign to make an expression equivalent to nine fifty.
Move the minus sign to the top of the second vertical line to get “10 to 10”, i.e. 9:50.
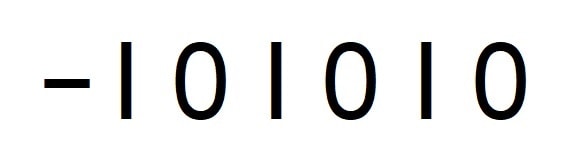
Please confirm you want to block this member.
You will no longer be able to:
Please allow a few minutes for this process to complete.
