Washing Dishes
A man is alone in his house washing dishes. When he looks down, there are more glasses in the sink than there were before. How come?
SOLUTION
The man’s pair of glasses fell inside the sink.
Category: Puzzles
We do not know where this puzzle originated from. If you have any information, please let us know via email.
Puzzle Sum 29
What measurement units do these sums spell?
SOLUTION
FOWL – OWL + BOOT – B = FOOT
INK – K + CHAIR + SHIP – AIRSHIP = INCH
Frustrating Question
John was asking Bob the same question again and again throughout the day and kept getting different answers. What was John’s question?
SOLUTION
John’s question was “What time is it?”.
Splitting Coins
You split 1000 coins into two piles and count the number of coins in each pile. If there are X coins in pile one and Y coins in pile two, you multiple the two numbers to get XY. Then you split both piles further, repeating the same counting and multiplication process, and adding the new multiplication results to the first one. The process ends when you end up with 1000 single-coin piles. Prove that you will always get the same final result, no matter how the piles have been divided during the splitting process.
For example, if you start with 5 coins and split them into a pile of 2 and a pile of 3, you get the number 2×3=6. Then, if you split the pile of 3 into a pile of 1 and a pile of 2, you will add 1×2=2 more to the 6 and get 8. Finally, if you split the two piles of 2 into single-coin piles, you will end up with 8+1+1=10.
SOLUTION
Consider the sum of the squares of the numbers of coins in each pile, plus twice the sum of the products. On each step, if you split a pile of X+Y coins into a pile of X coins and a pile of Y coins, the sum of the squares will get reduced by 2XY, exactly the amount the sum of the products will increase by. Therefore, that number remains constant throughout the entire process and ends up exactly (1000²-1000)/2=499500.
Puzzle Sum 28
What animals do these sums spell?
SOLUTION
SLOTH + HARROW – ARROW = SLOTH
FERRULE – RULE + VINE + GARRET – VINEGAR = FERRET
1 to 8 on a Cube
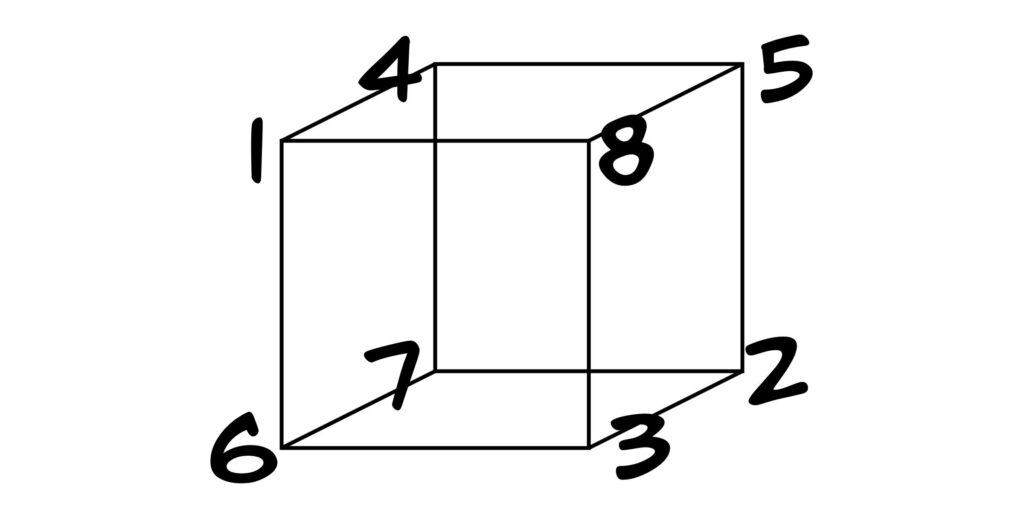
Place the numbers from 1 to 8 on the vertices of a cube so that the sum of the four numbers on every face is the same.
SOLUTION
The solution is shown below:
Sequence 1, 3, 7, 12
Which is the next number in the following sequence:
1, 3, 7, 12, 18, 26, 35, 45, 56, ?
SOLUTION
This is the so called Hofstadter Figure-Figure Sequence.
The sequence of the differences between the consecutive numbers in the original sequence is 2, 4, 5, 6, 8, 9, 10, 11… These are exactly the natural numbers missing from the original sequence. Therefore, the next number should be 56 + 13 = 69.
A Cardinal Points
A cardinal points and says, “thorn, shout, seat, and stew.” Can you explain?
SOLUTION
The sentence is a play on words and anagrams. Thorn, shout, seat, and stew are anagrams of the four cardinal directions of the compass: north, south, east, and west.
One Hundred Rooms
There are 100 rooms in a row in a building and inside each room there is a lamp that is turned off. One person enters each room and switches the lamp inside. Then, a second person enters every second room (2, 4, 6, etc.) and switches the lamp inside. A third person switches the lamp in every third room and so on and so far, until person #100 switches the lamp in room 100. How many lamps are turned on at the end?
SOLUTION
We can see that the only switches that have been switched an odd number of times are the ones in rooms with perfect square numbers.
Indeed, if person N has switched the switch in room M, then person M/N has done that as well. Since person N and M/N coincide only when M=N², the claim above follows.
We conclude that the number of lamps that are turned at the end is equal to the number of perfect squares less than or equal to 100; that is exactly 10 rooms.