Category: Puzzles
Shark Attack
A man stands in the center of a circular field which is encompassed by a narrow ring of water. In the water there is a shark which is swimming four times as fast as the man is running. Can the man escape the field and get past the water to safety?

Yes, he can. Let the radius of the field is R and its center I. First the man should start running along a circle with center I and radius slightly less than R/4. His angular speed will be larger than the angular speed of the shark, so he can keep running until gets opposite to it with respect to I. Then, the man should dash away (in a straight line) towards the water. Since he will need to cover approximately 3R/4 distance and the shark will have to cover approximately 3.14R distance, the man will have enough time to escape.
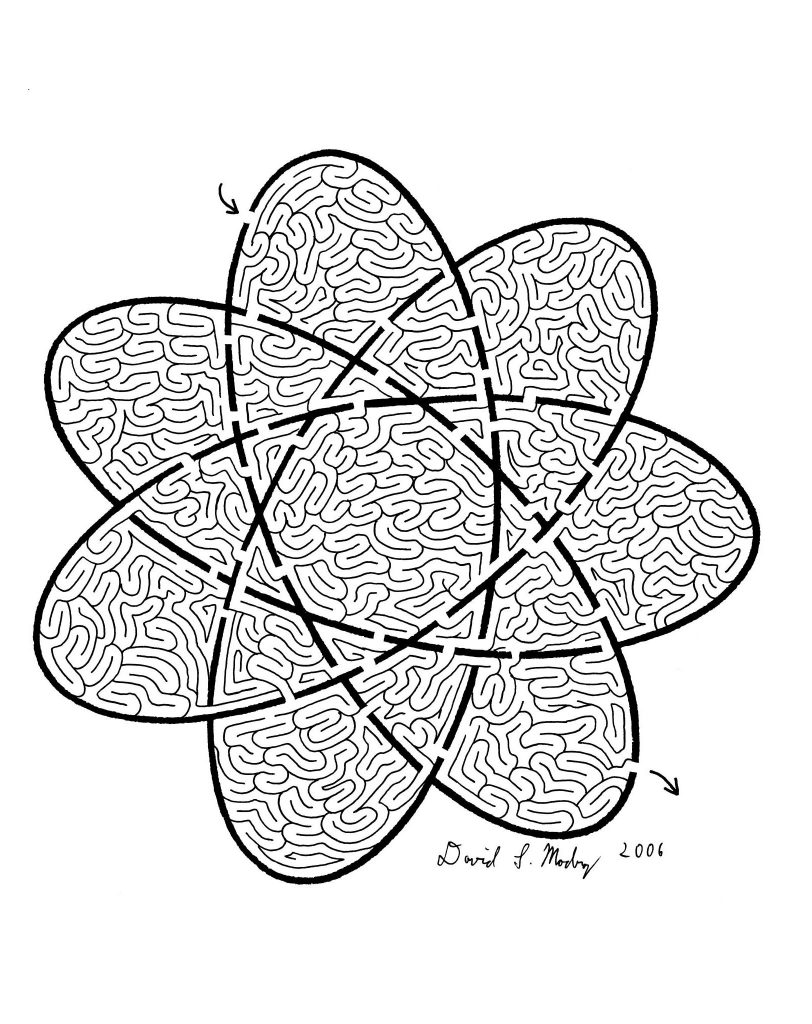
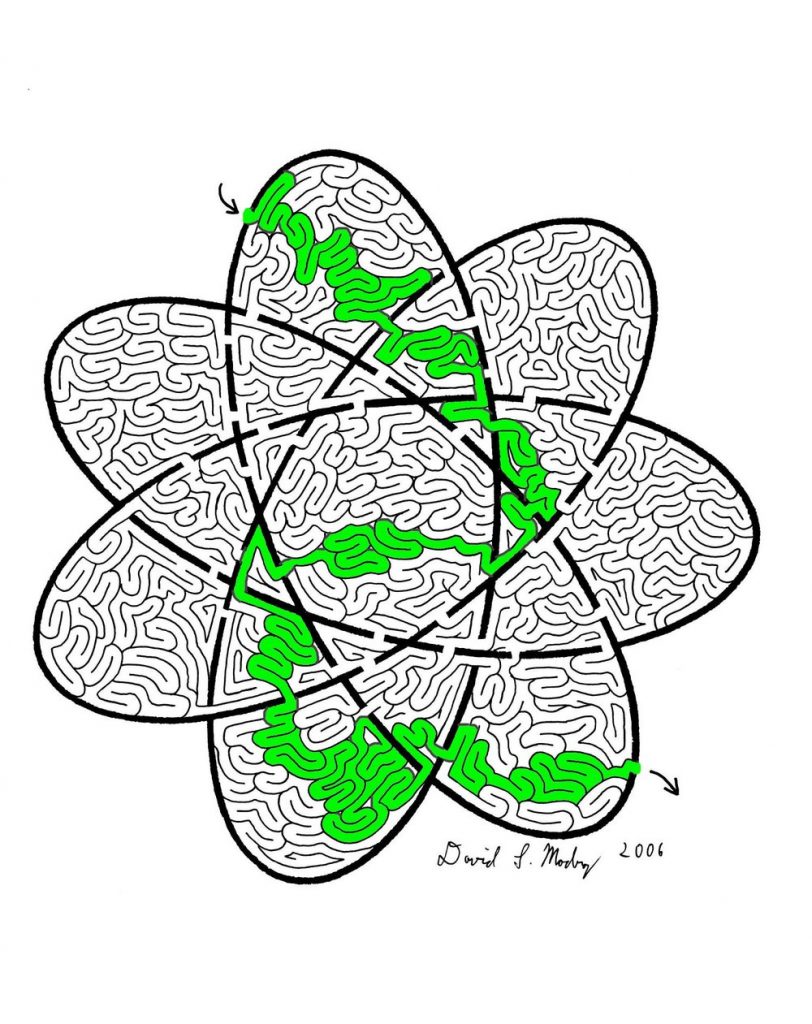
Sequence 1, 11, 21, 1112
What follows next in the following sequence:
1, 11, 21, 1112, 3112, 211213, 312213, ?
Every term in the sequence describes how many 1s, 2s, 3s, etc. were there in the previous term. “11” means that in the previous term there was one 1. “21” means that in the previous term there were two 1s. “1112” means that in the previous term there were one 1 and one 2. “3112” means that in the previous term there were three 1s and one 2. “211213” means that in the previous term there were two 1s, one 2 and one 3. “312213” means that in the previous term there were three 1s, two 2s and one 3. Therefore, the next number in the sequence should be 212223.
Gods of Truth
You encounter three Gods in a room – the God of Truth, the God of Lie and the God of Uncertainty. You don’t know which one is which, but know that the God of Truth always says the truth, the God of Lie always says the lie and the God of Uncertainty sometimes lies and sometimes says the truth. You can ask in succession each of the Gods a unique question, to which they can reply only with “Yes” or “No”. However, their responses will be in their native language – “Da” or “Ne”, and you don’t know which translation to which answer corresponds. Your task is to figure out what questions to ask the Gods, so that will recognize which one of them is the God of Truth, which one is the God of Lie and which one is the God of Uncertainty.
Label the gods with numbers – 1, 2, and 3.
First, ask god 1 “If I ask you whether god 2 is random, would you say ‘Da’?”. If he responds “Da”, then god 3 is not the god of uncertainty. If he responds “Ne”, then god 2 is not the god of uncertainty. In both cases we will be able to find a god which is not the god of uncertainty, let without of generality that is god 3.
Next, ask god 3 “If I ask you whether you are the God of Lie, would you say ‘Da’?”. If he says “Da”, then he is the God of Truth. If he says “No”, then he is the God of Lie.
Finally, ask god 3 whether god 1 is the God of Uncertainty and conclude the identities of all gods.
My Son
After a car accident, the father dies and the boy arrives at the emergency room in the hospital. Upon entering the room however, the surgeon exclaims “This is my son, I can’t operate!” How is this possible?
The surgeon is the mother of the boy.
The Fragile Bridge
You have to cross a long bridge which supports weight up to 180 pounds. However, you weigh 175 pounds and also carry with yourself 3 golden eggs, each of which weighs 2 pounds. How can you get to the other side?
P. S. If you leave an egg unattended, someone can steal it.
Simply juggle the eggs while crossing the bridge.
The Monty Hall Show
You are in Monty Hall’s TV show where in the final round the host gives you the option to open one of three boxes and to receive the reward inside. Two of the boxes contain just a penny, while the third box contains $1.000.000. In order to make the game more exciting, after you pick your choice, the rules require the host to open one of the two remaining boxes, such that it contains a penny inside. After that he asks you whether you want to keep your chosen box or to switch it with the third remaining one. What should you do?
This is the so called “Monty Hall” problem. The answer is that in order to maximize your chances of winning $1.000.000, you should switch your box. The reason is that if initially you picked a box with a penny, then after switching you will get a box with $1.000.000. If initially you picked a box with $1.000.000, then after switching you will get a box with a penny. Since in the beginning the chance to get a penny is 2/3, then after switching your chance to get $1.000.000 is also 2/3. If you stay with your current box, then your chance to get $1.000.000 will be just 1/3.
Optical Illusions
If you count carefully the number of people before the tiles scramble and after that, you will see that one person disappears. Can you explain how this is possible?
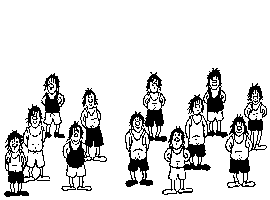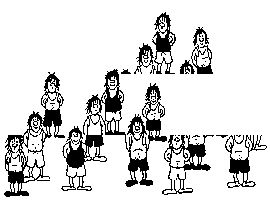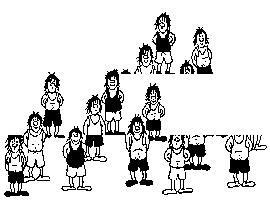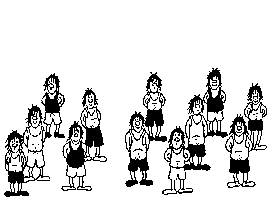
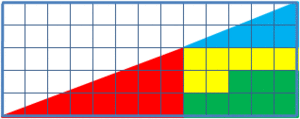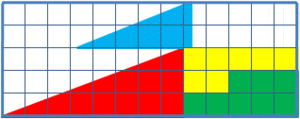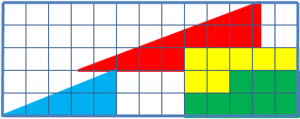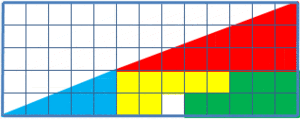
Similarly, in this picture it looks like after changing the places of the tiles in the diagram, their total area decreases by one. Can you explain this?
If you look carefully, you will notice that every person in the picture of 12 people is slightly taller than the corresponding person in the picture of 13 people. Basically, we can cut little pieces from 12 different people without making noticeable changes and arrange them into a new person.
For the second question, none of the shapes before and after the scrambling is really a triangle. One of them is a bit curved in at the hypotenuse and the other one is a bit curved out. This is barely noticeable, because the red and the blue triangle have very similar proportions of their sides – 5/2 ~ 7/3.
Pinned Men
The following game is played under very specific rules – no pinned piece checks the opposite king. How can White mate Black in 2 moves?

First, White plays f3 and threatens mate with Qxe2. Indeed, blocking with the black rook on d4 will not help, because it will become pinned, which means that the rook on d6 will become unpinned, which will make the bishop on b6 pinned, and that will unpin the knight on c7, resulting in a mate. Below are listed all variations of the game.
1. … Rd5 2. Qxe2#
2. … Bxa5 2. Kc8#
3. … Bxc7 2. Nxc7#
4. … Bxe8 2. Kxe8#
5. … Qxe7+ 2. Kxe7#
6. … Rd2 2. Bxd2#
7. … Rxd6+ 2. Qxd6#
3 Men, 1 Woman
Warning: this puzzle involves mature themes that are inappropriate for younger audiences. If you are not an adult, please skip this puzzle.
3 men must have sex with 1 woman, but they have only 2 condoms. Each of the 4 people has some unique STD which they don’t want to transfer to the rest. What can they do?
They can start by putting the two condoms on top of each other and letting the first man use them. After that, the second man can take the inner condom out and use just the outer condom. Finally, the third man can take the removed inner condom, turn it inside out, and place it back inside the outer condom. Then he, he can use the two condoms simultaneously.