Behind
Bruce is standing behind Tony and Tony is standing behind Bruce. How is this possible?
SOLUTION
Bruce and Tony are standing back to back.
Category: Puzzles
We do not know where this puzzle originated from. If you have any information, please let us know via email.
Greater Than God
What is greater than God, more evil than the Devil, the poor have it and the rich need it?
SOLUTION
The answer is NOTHING.
3 by 3
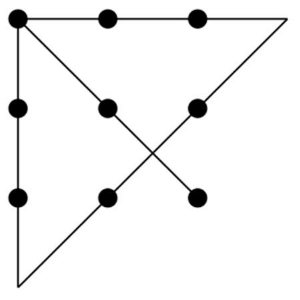
Can you draw a path consisting of 4 line segments which passes through all points in the grid?
SOLUTION
Yes, you can, as shown on the picture below.
Hamster Time
In order to escape this room, your hamster must
SOLUTION
The solution is shown below.
The White House
If Mr. Green lives in the green house and Mr. Red lives in the red house, who lives in the White House?
SOLUTION
The President.
$5 Bill
Bern tells Sandy, “This isn’t the $20 bill you left on the table. It is mine – I was keeping it between pages 15 and 16 of my textbook.”
Sandy retorts, “You are lying and I can prove it.” How does she know?
SOLUTION
Pages 15 and 16 are on the same sheet of paper in the textbook (just like pages 1 and 2 are) and therefore the bill couldn’t be between them.
Water with Ice
You have a glass of water and an ice cube floating in it. When the ice cube melts, will the water level increase, decrease or remain the same?
SOLUTION
It will remain the same. The amount of water that the ice cube displaces is equal to its mass. Since the mass does not change and the density of water is equal to 1, the extra water after melting will be the same amount as the displaced water before that.
FEATURED
Heads Up, Heads Down
You are blindfolded and on the table, in front of you, 50 coins are placed. You are told that X of them are heads up and the rest are heads down. Then you are asked to separate the coins into two groups and optionally flip some of them so that the number of heads in both groups becomes the same. How can you do this?
SOLUTION
Separate the coins into one group of X coins and into another group of 50-X coins, then flip every coin in the first group. If in the first group there were Y heads up initially, then after flipping there would be X-Y – exactly the number of heads up in the second group.
The Man in the Photo
A person is looking at somebody’s photo and exclaims:
“Brothers and sisters, I have none,
But this man’s father is my father’s son.”
Who is the person in the photo?
SOLUTION
It is the person’s son.
Mixed Up Pills
One patient has two bottles with 30 pills each and every night has to take one pill from each of the bottles. Unfortunately one night after he takes out a pill from the first bottle and places it on the table, by accident drops two pills from the second bottle right next to it. The pills look identical, so he can not differentiate them. It is very important that he continues his treatment diligently throughout the entire timespan of 30 days. What should the patient do?
SOLUTION
The patient should keep taking one pill from each bottle until there are 4 pills remaining – 1 in the first bottle and 3 on the table. On the 29th day he splits the pills in halves and takes one half from each pill. On the 30th day he takes the remaining halves of the pills.