Thoka’s Rebus 6
Can you figure out which words are depicted by these rebuses?
SOLUTION
The answers are SKYLINE, HEADQUARTERS, RAINBOW, and EYELID.
Category: Puzzles
Thoka Maer is a German artist who creates illustrations and short animations. Her scope of work runs the gamut from the figurative/narrative to the abstract/surreal, though it is held together by the consistent use of pencil and crayon.
Ants Maze
Find a non-intersecting closed path, passing through all four ants, which traverses this double-sided maze. You can not switch between the top and the bottom side of the path at any times.
SOLUTION
The solution is shown below.
FEATURED
Prisoners and Boxes
There are 100 inmates living in solitary cells in a prison. In a room inside the prison there are 100 boxes and in each box there is a paper with some prisoner’s name (all different). One day the warden tells the prisoners that he has aligned next to the wall in a special room 100 closed boxes, each of them containing some prisoner’s name (all different). He will let every prisoner go to the room, open 50 of the boxes, then close them and leave the room the way it was, without communicating with anybody. If all prisoners find their names in the boxes they open, they will be set free, otherwise they will be executed. The prisoners are allowed to come up with a quick plan before the challenge begins. Can you find a strategy which will ensure a success rate of more than 30%?
SOLUTION
The prisoners can assign numbers to their names – 1, 2, 3, … , 100. When prisoner X enters the room, he should open first the X-th box in the line. If he sees inside prisoner’s Y name, he should open next the Y-th box in the line. If he sees in it prisoner’s Z name, he should open next the Z-th box in the line and so on.
The only way which will prevent all prisoners from finding their names is if there is a long cycle of boxes (length 51 or more), such that the first box in the cycle directs to the second box in it, the second box to the third box, the third box to the fourth box and so on.
It is not hard to compute that the probability of having a cycle of length K>50 is exactly 1/K. Then the probability for failure will be equal to the sum 1/51 + 1/52 + … + 1/100, which is very close to ln(100) – ln(50) = ln(2) ~ 69%. Therefore, this strategy ensures a success rate of more than 30%.
FEATURED
Gun Duel
Mick, Nick, and Rick arrange a three-person gun duel. Mick hits his target 1 out of every 3 times, Nick hits his target 2 out of every 3 times, and Rick hits his target every time. If the three are taking turns shooting at each other, with Mick starting first and Nick second, what should be Mick’s strategy?
SOLUTION
Clearly, Mick should not aim for Nick, because if he kills him, then he will be killed by Rick. Similarly, Nick should not aim for Mick, because if he kills him, then he also will be killed by Rick. Therefore, if Rick ends up against alive Mick and Nick, he will aim at Nick, because he would prefer to face off a weaker
Thus, if Mick shoots at Rick and kills him, then he will have to face off Nick with chance of survival less than 1/3. Instead, if he decides to shoot in the air, then he will face off Nick or Rick with chance of survival at least 1/3. Therefore, Mick’s strategy is to keep shooting in the air, until he ends up alone against one of his opponents.
Four Chains
You have four metal chains and each of them has three links. What is the minimal number of cuts you need to make so that you can connect the chains into one loop with twelve links?
SOLUTION
You need only three cuts – cut all the links of one of the chains and then use them to connect the ends of the remaining three chains.
Falling Baby
How can a baby fall out of a 30-story building onto the ground and still be alive?
SOLUTION
The baby fell from the first floor.
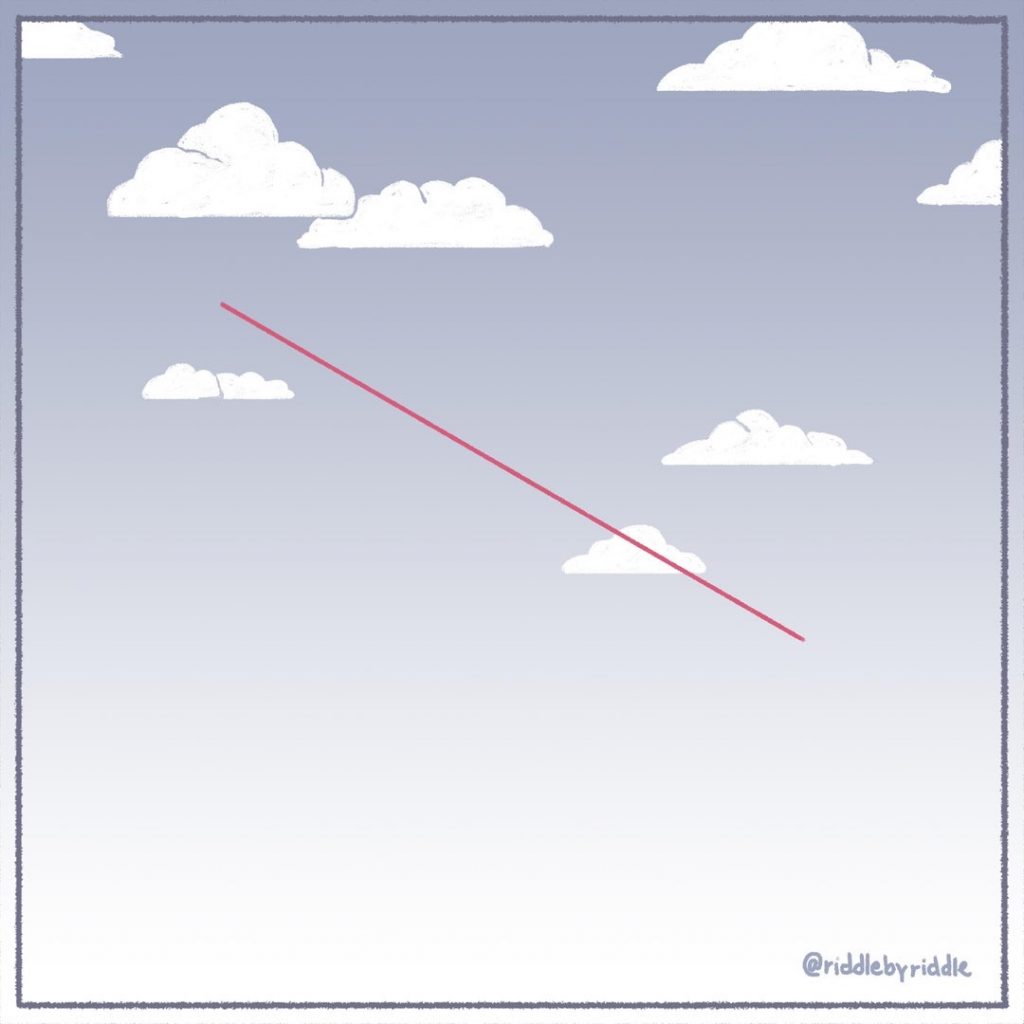
The Number in the Yellow Circle
Which is the missing number in the yellow circle?
SOLUTION
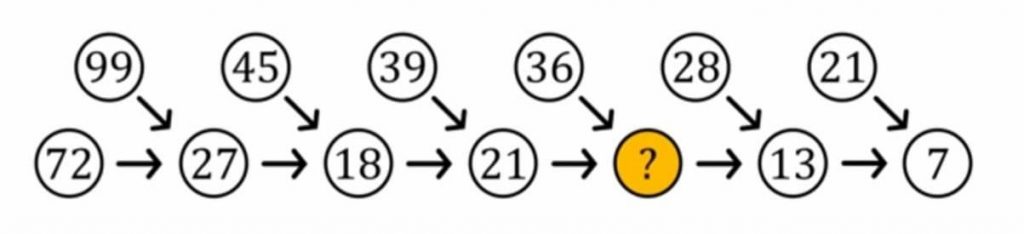
The missing number is 12. Each number is equal to the sum of the digits of the numbers pointing towards it.
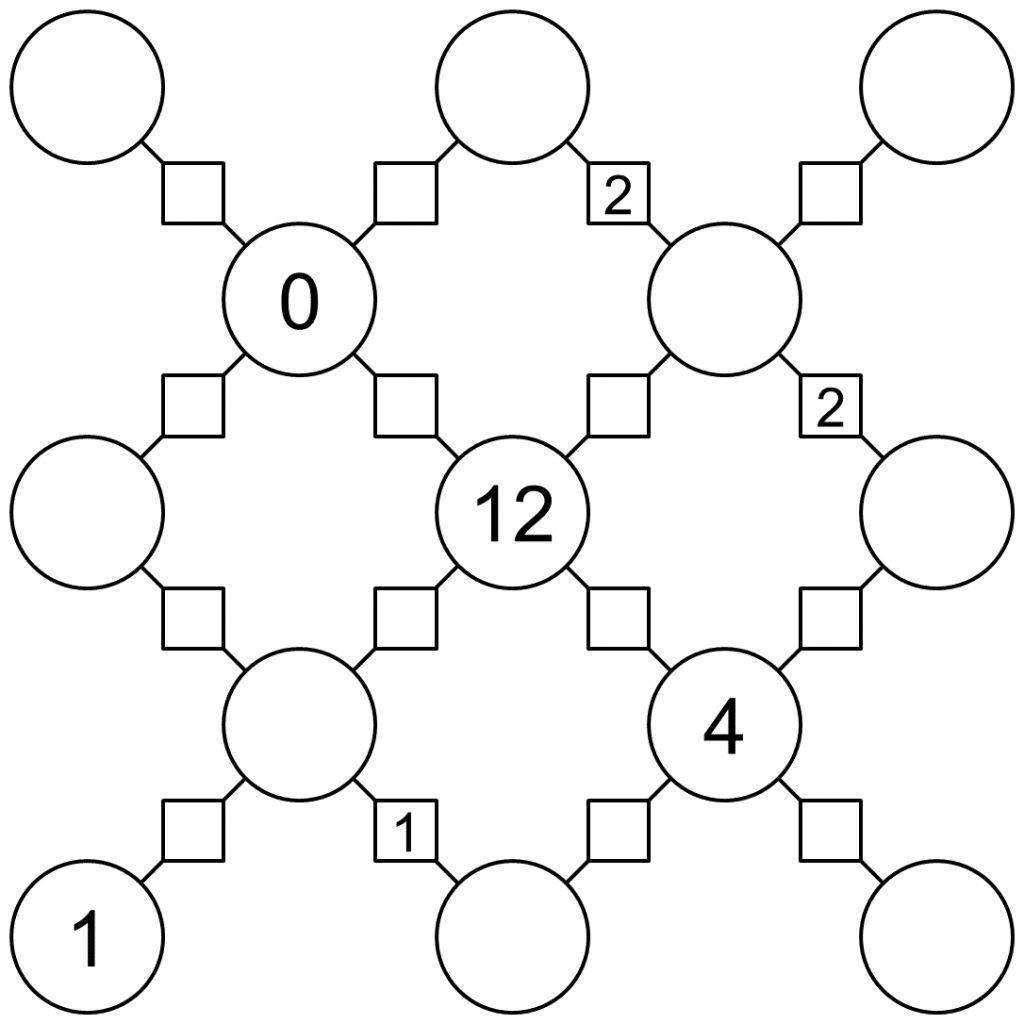
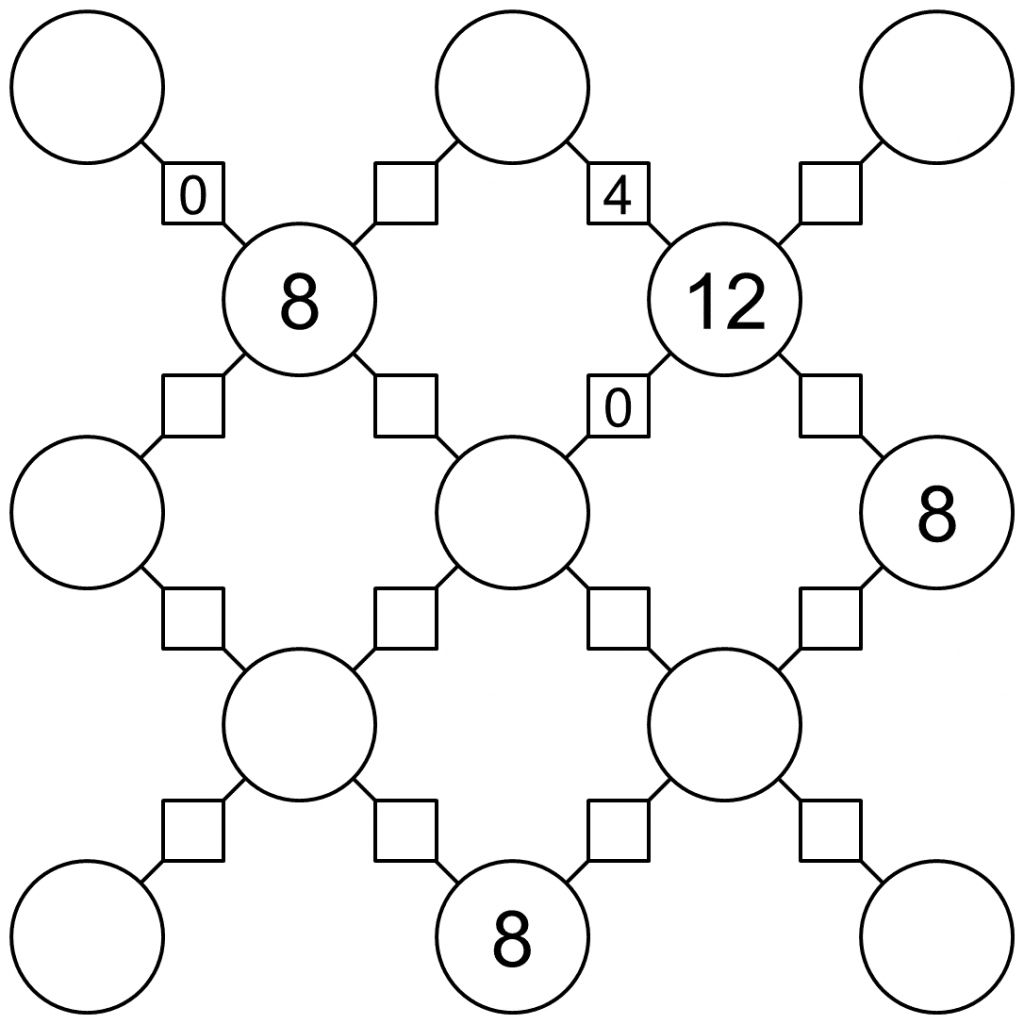
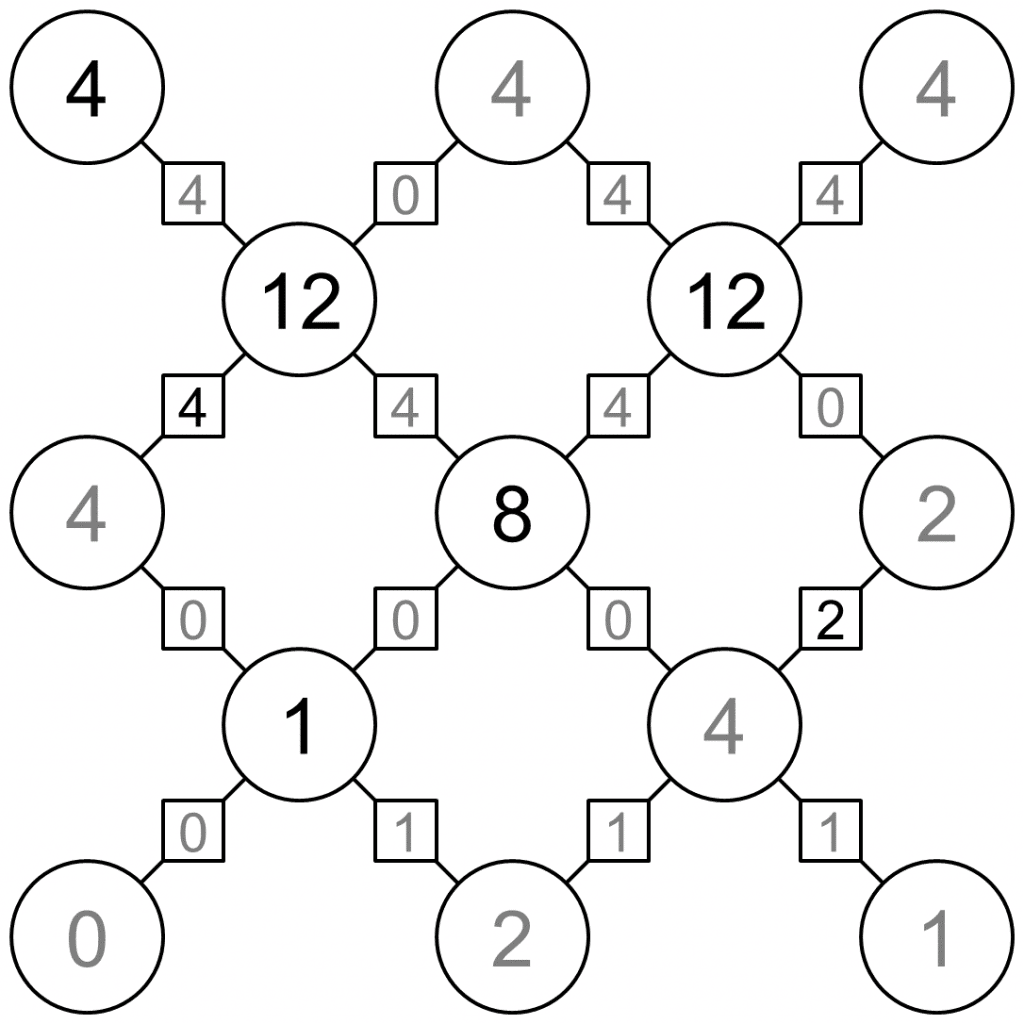
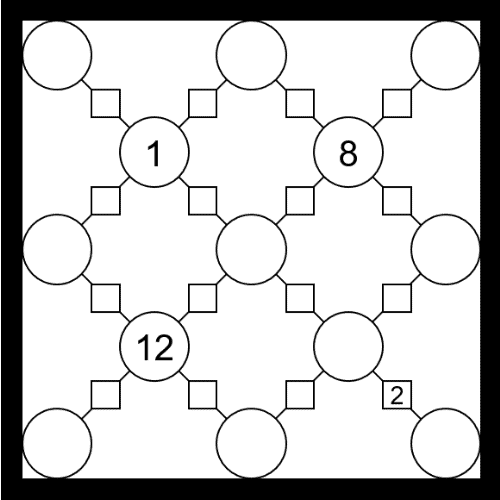
Vinculus Puzzles
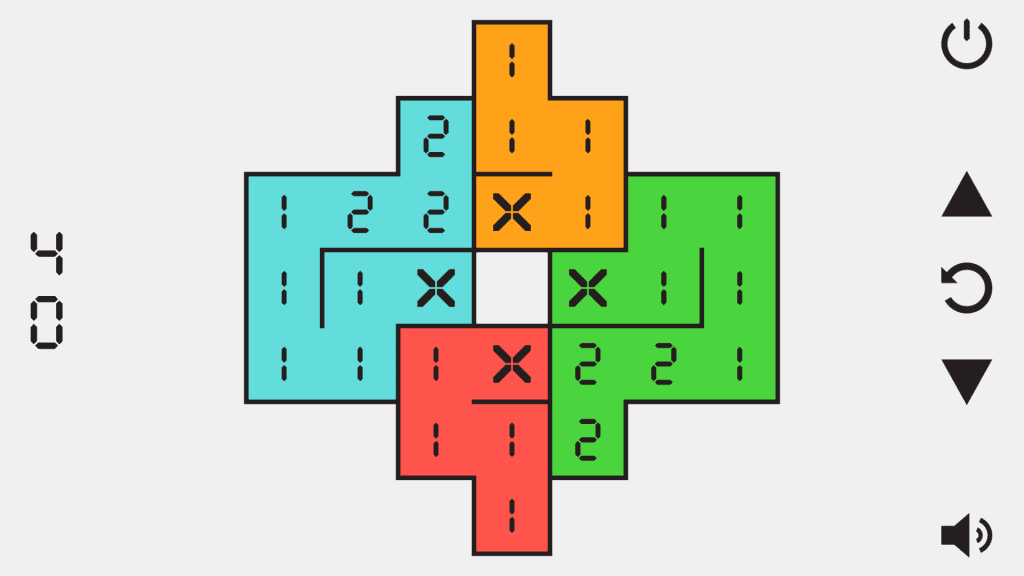
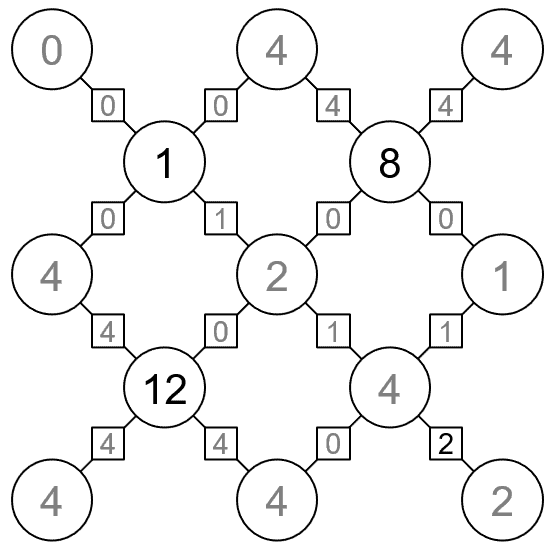
Circles are particles and lines joining them are bonds. The objective is to find all the hidden values, following these four rules:
- Particle values must be the sum of their bond values.
- Particles can have the following values: 0, 1, 2, 4, 8, 12, 16.
- Bonds can have the following values: 0, 1, 2, 4.
- If two particles have the same value, the bond between them must have value 0.
EASY 
MEDIUM 
HARD
SOLUTION
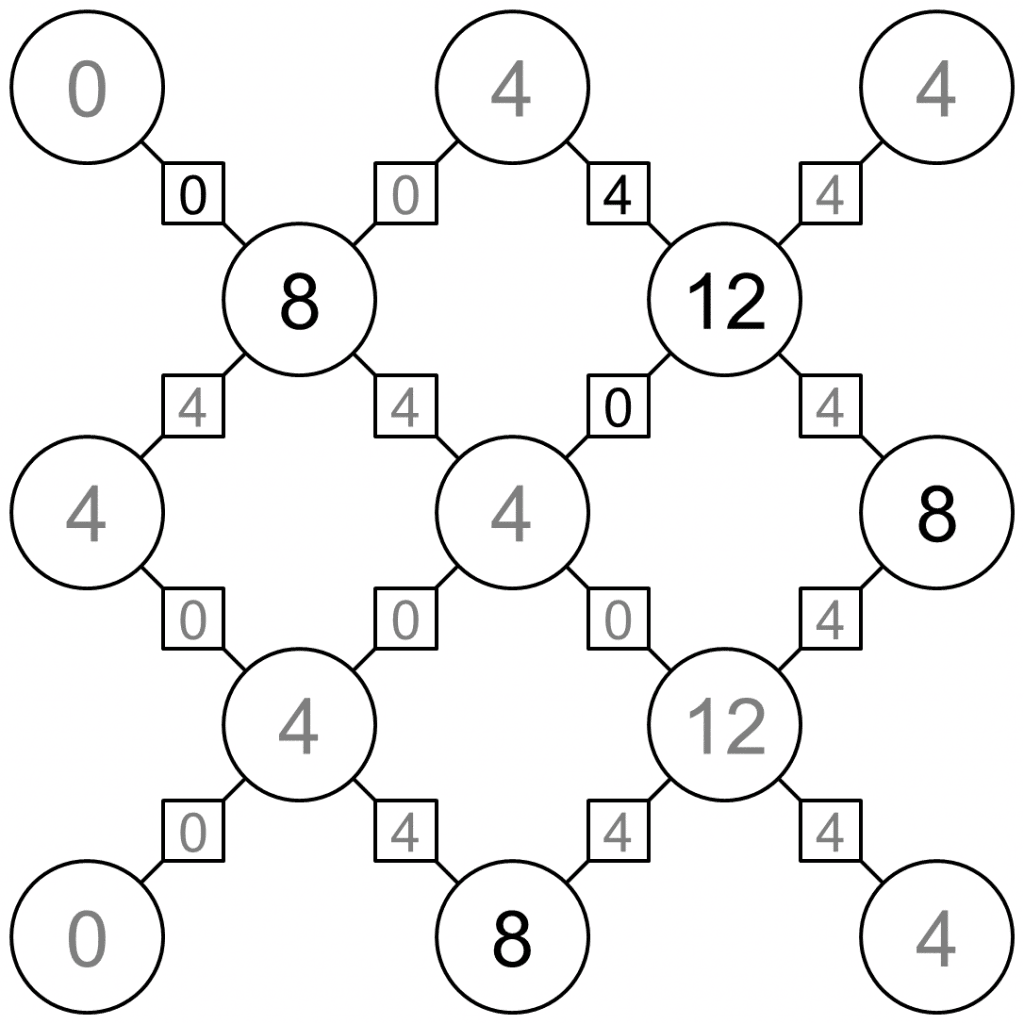
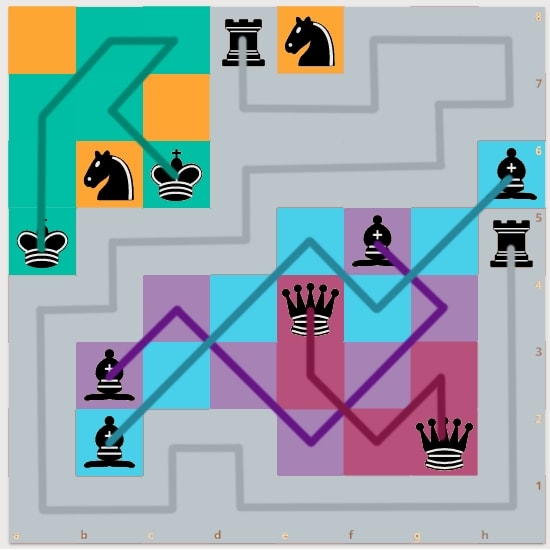
The solutions are shown below.
FEATURED
Puzzle Tournament 3
Puzzle Prime’s third puzzle tournament was organized on January 31, 2021. Congrats to Elyot G. who is once again a winner! You can see the problems and the rankings below.
You have 60 minutes to solve 5 puzzles, each worth 1 point. Upload your solutions as a pdf, document, or image, using the form below. Good luck!
Time for work: 1 hour
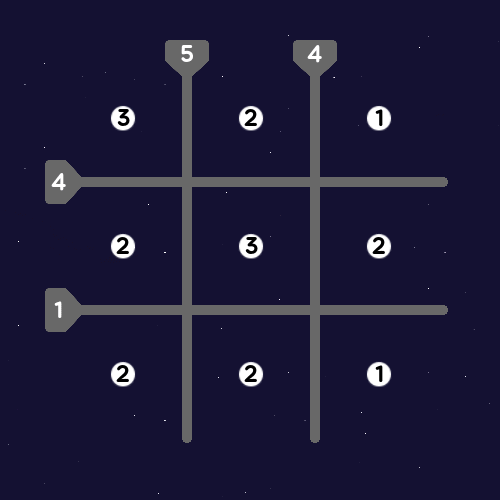
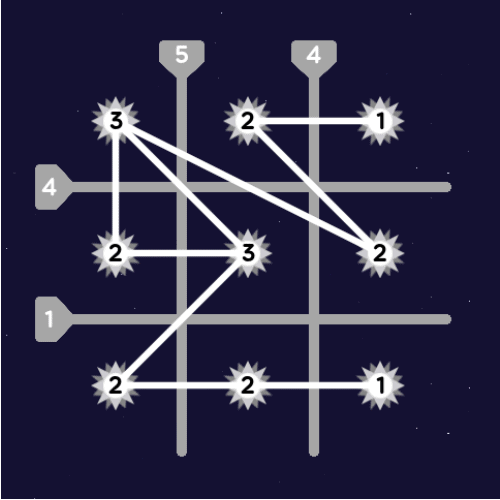
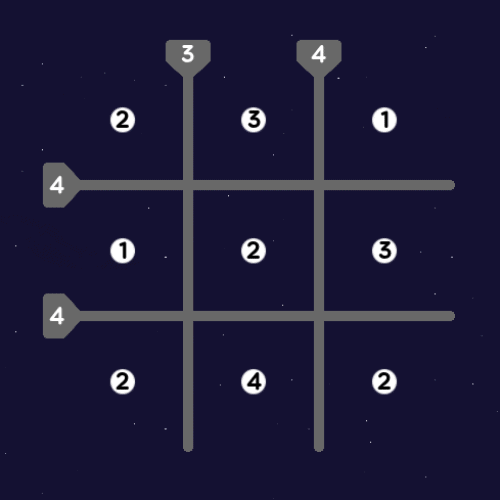
1. Constellation
by Raindrinker
Connect the stars with lines, so that the number inside each star corresponds to the number of lines connected to it, and the number in each barrier corresponds to the number of lines intersecting it.
Note: The stars in the corners cannot be connected, since the lines would pass through other stars.
SHOW EXAMPLE
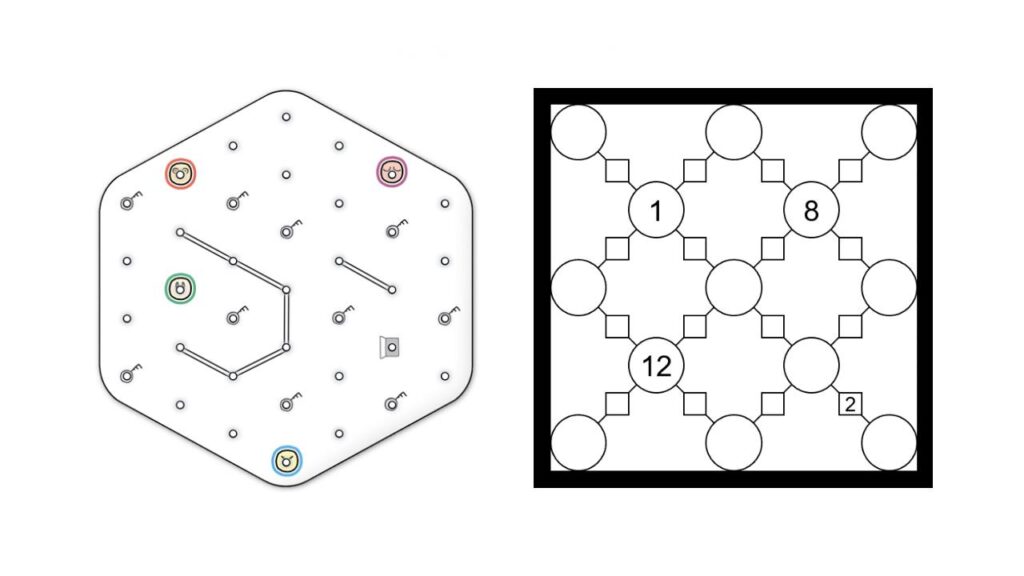
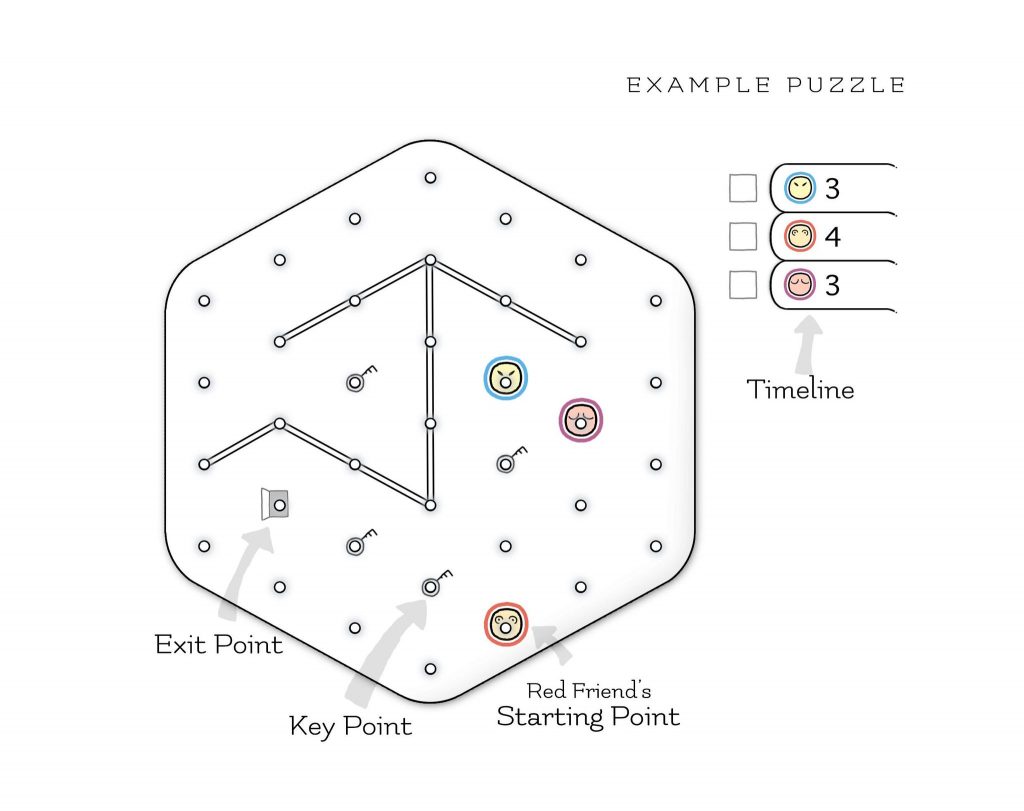
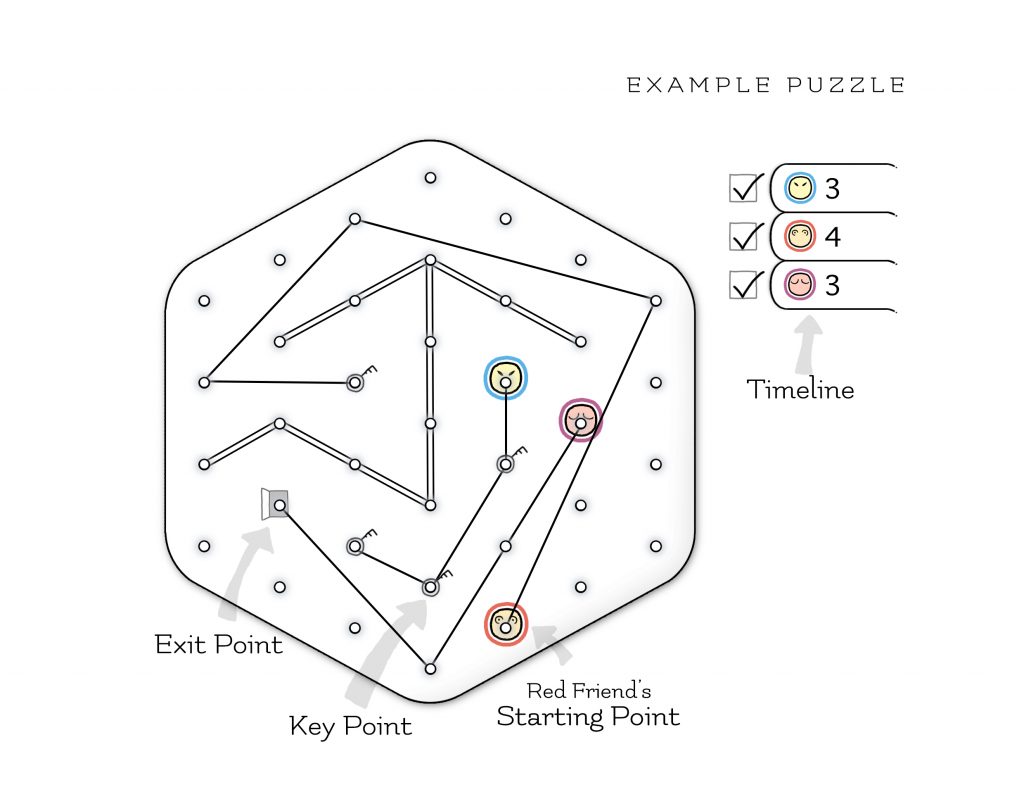
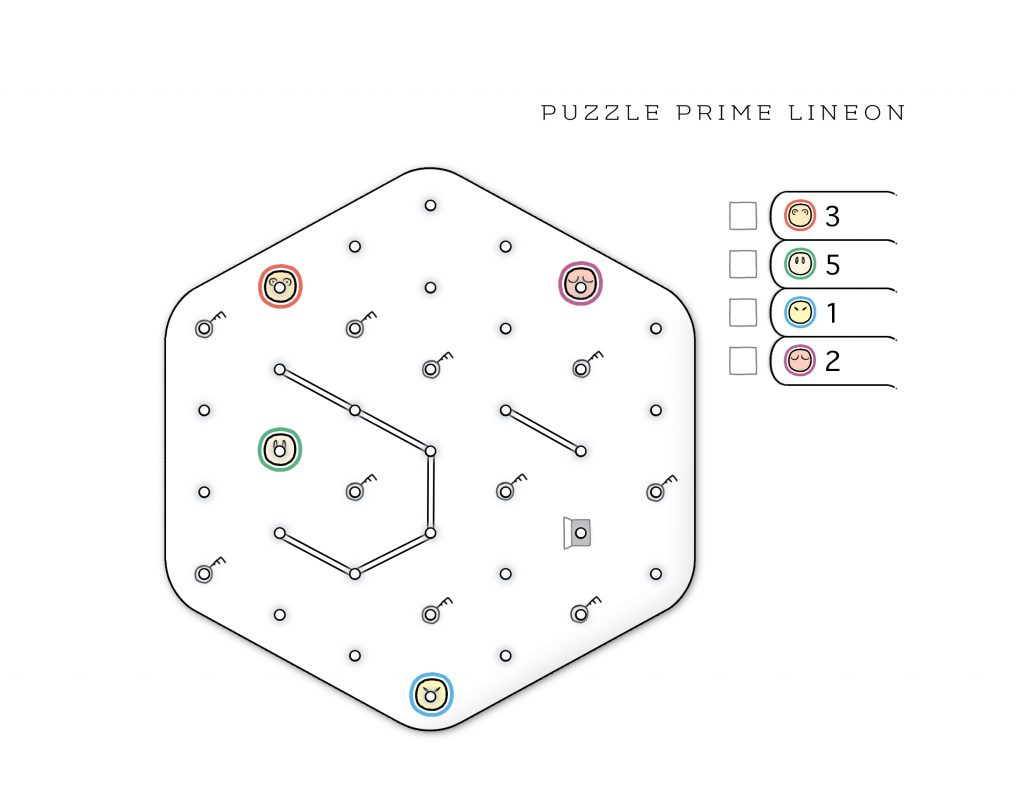
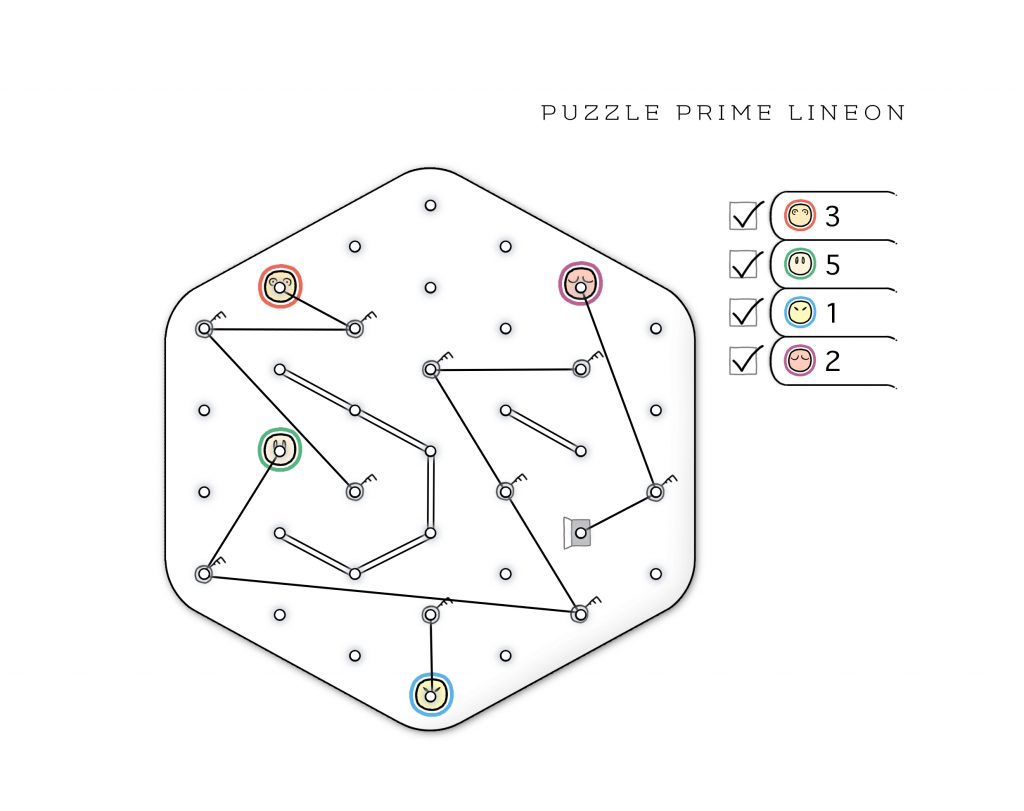
2. Lineon
by Blaž Gracar
GOAL:
Move one of the Friends to the Exit Point.
PLAYING THE GAME:
Draw lines to move Friends. A move is connecting a point on the Grid to another point on the Grid by drawing a straight line. The line can be made in any direction, as long as it connects exactly two points and doesn’t cross or touch another line.
TIMELINE:
You move each Friend as many times as it says on the Timeline, starting with the topmost Friend and continuing in the order all the way down to the bottom one.
KEY POINTS, EXIT POINT, AND WALLS:
One of the Friends must move to the Exit Point, but before he does that, each of the Key Points must be already connected with a line. A Wall is a double line and no Friend can cross or touch it.
SHOW EXAMPLE
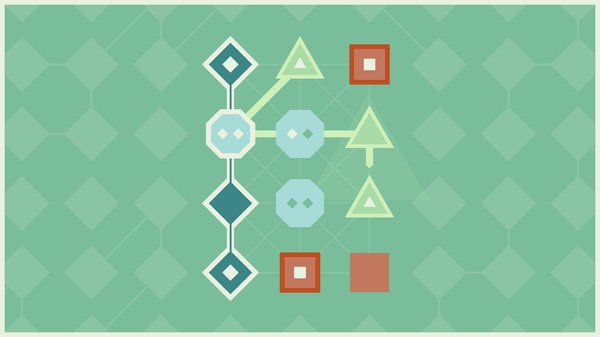
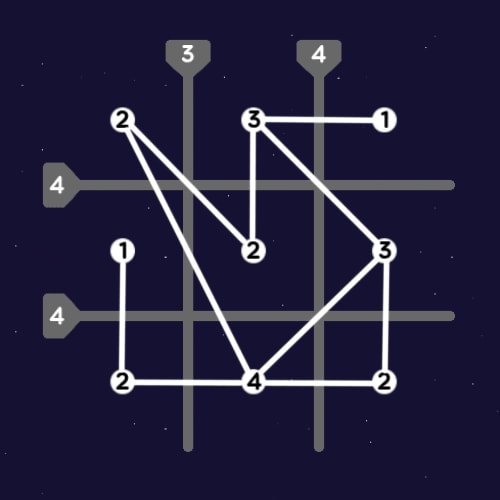
3. Vinculus
by Dr. DJ Upton
Circles are particles and lines joining them are bonds. The objective is to find all the hidden values, following these four rules:
- Particle values must be the sum of their bond values.
- Particles can have the following values: 0, 1, 2, 4, 8, 12, 16.
- Bonds can have the following values: 0, 1, 2, 4.
- If two particles have the same value, the bond between them must have value 0.
SHOW EXAMPLE
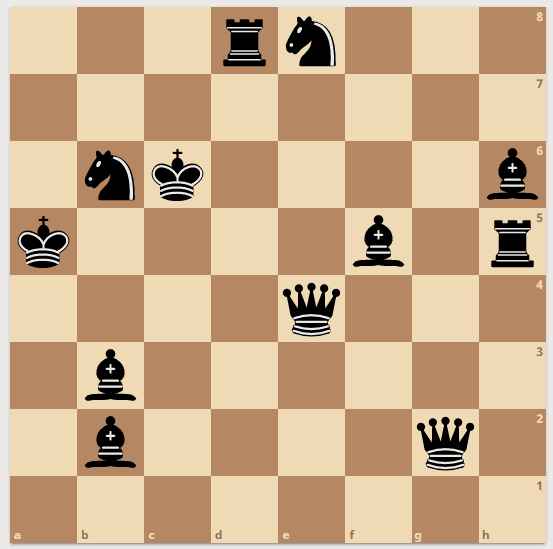
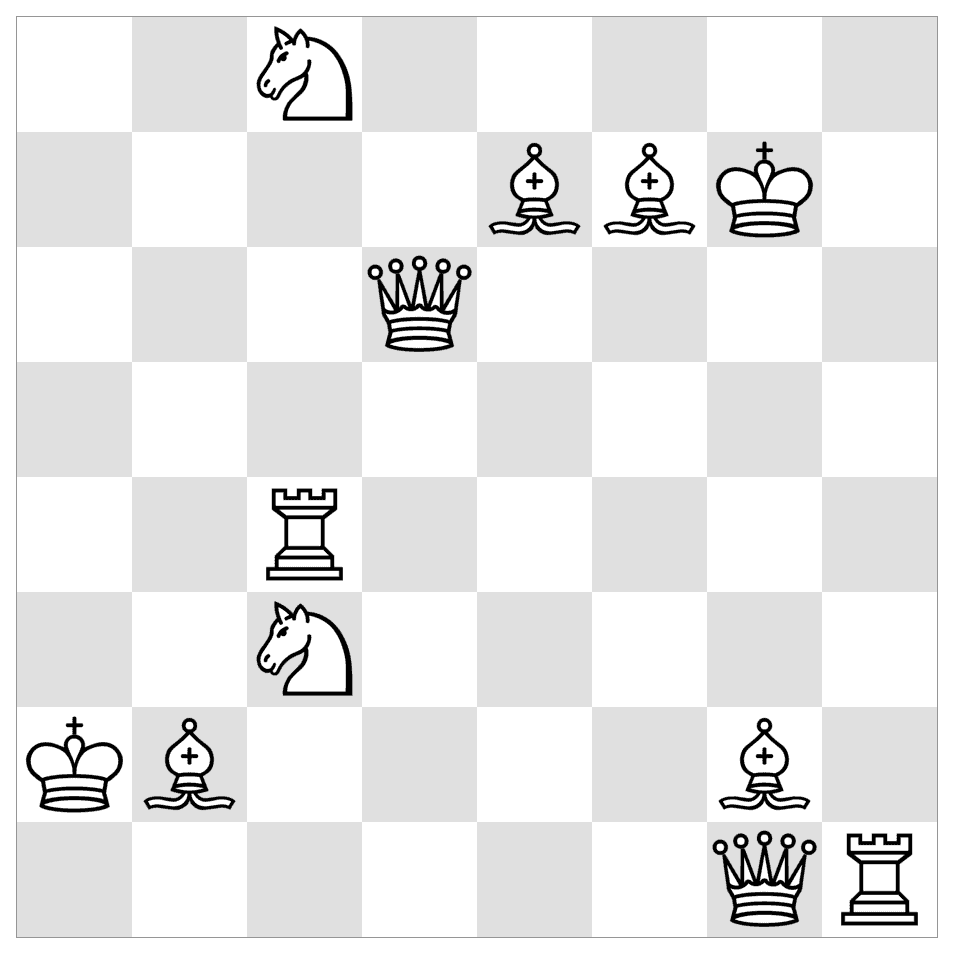
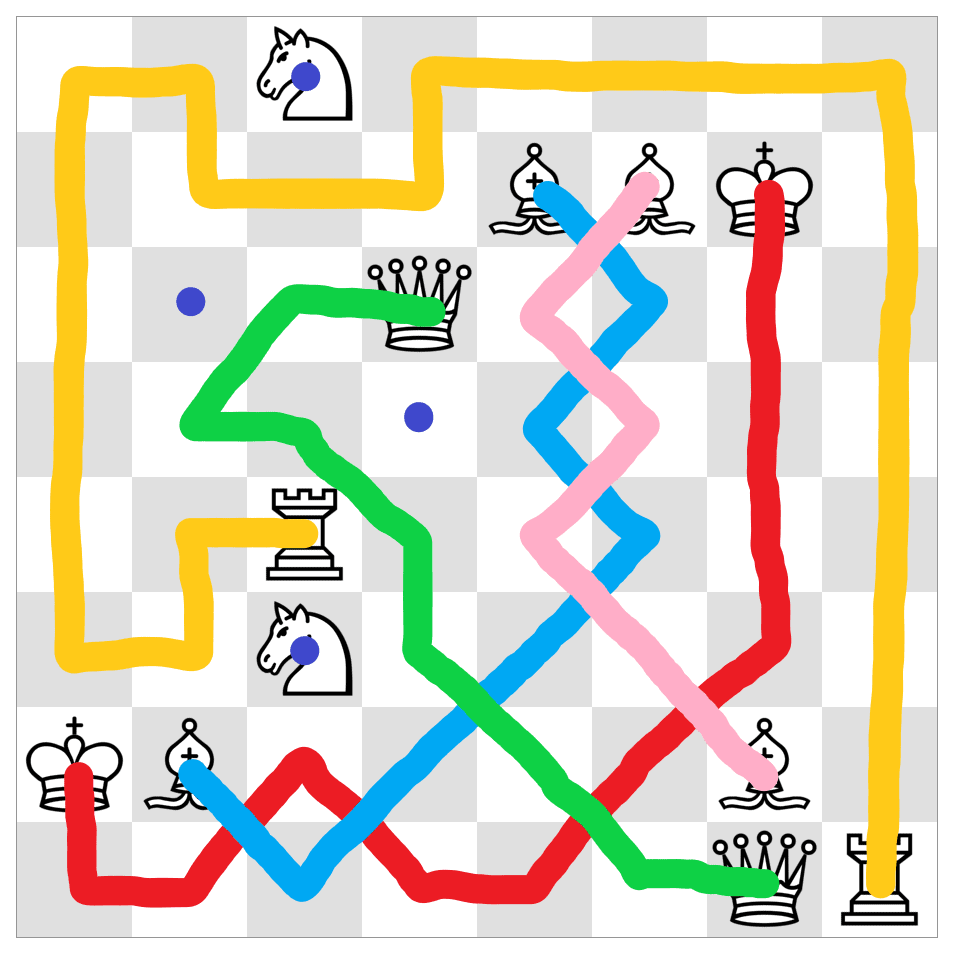
4. Chess Connect
by Puzzle Prime
The starting and ending positions of 6 chess pieces are shown on the board. Find the trajectories of the pieces, if you know that they do not overlap and completely cover the board.
Notes: The pieces can not backtrack. Two trajectories can intersect diagonally but can not pass through the same square. Only the Knight has a discontinuous trajectory.
SHOW EXAMPLE
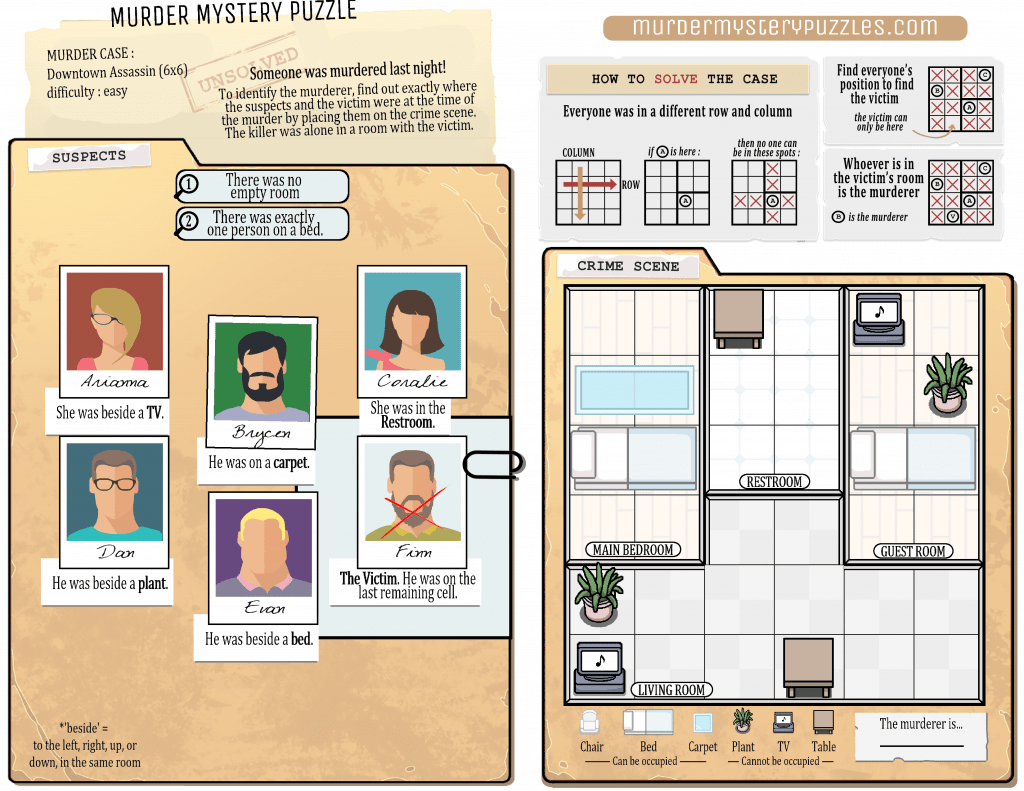
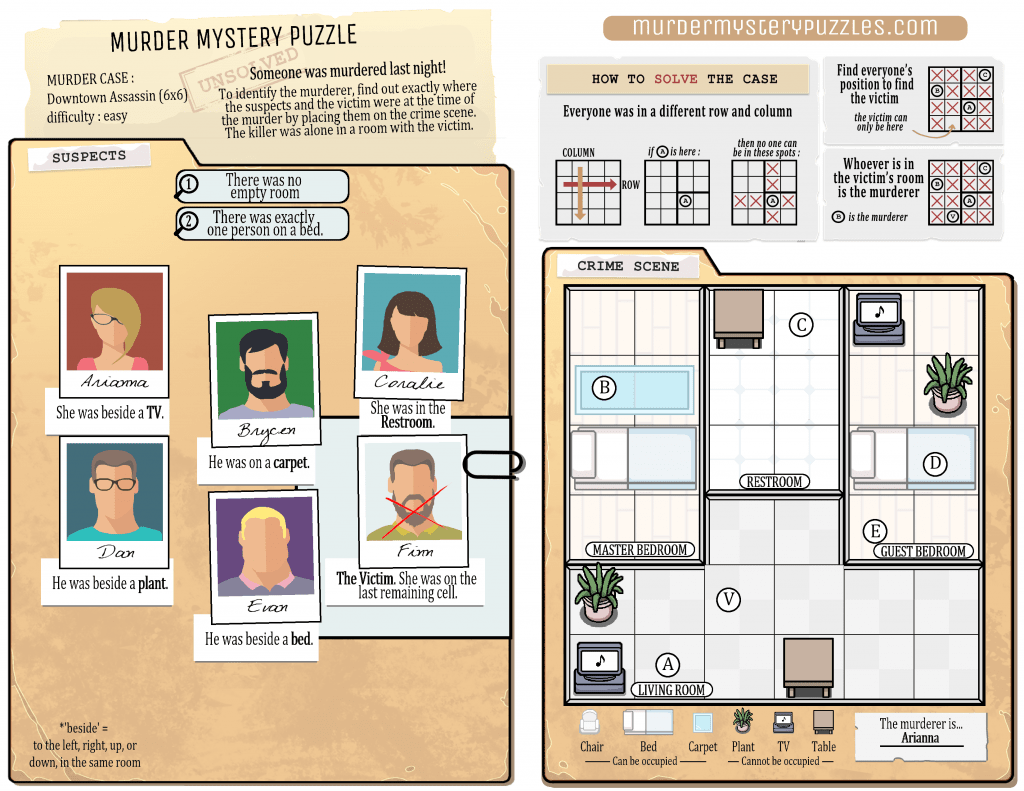
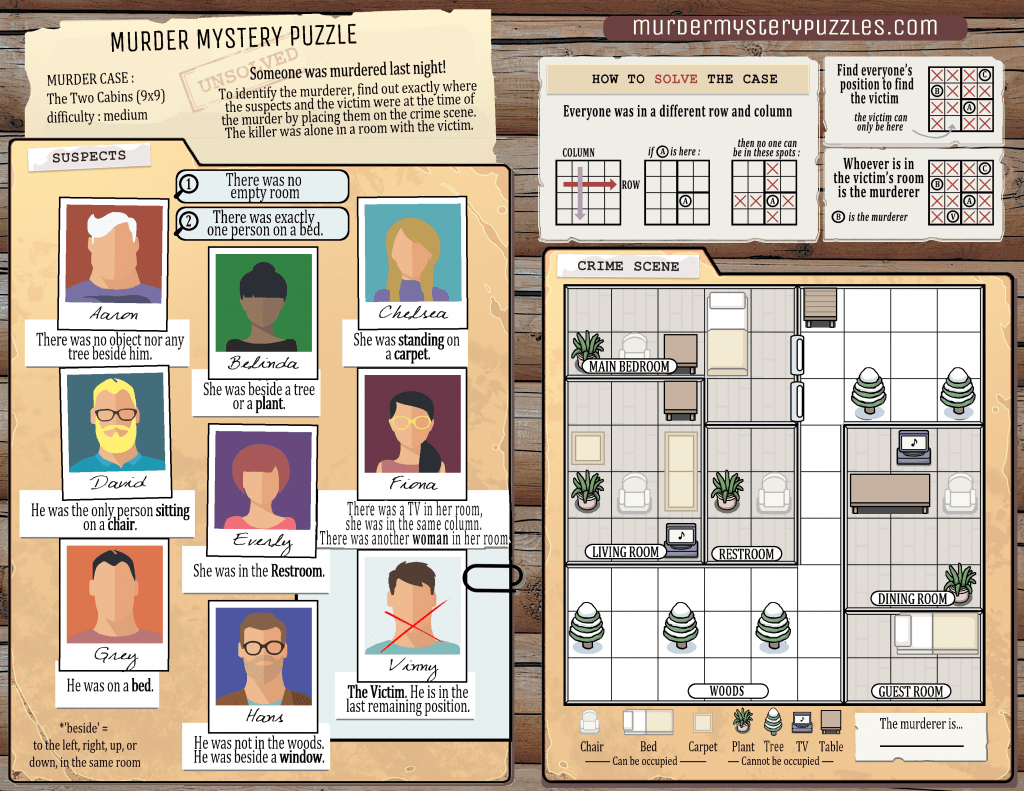
5. Murder Mystery
by Hiroji Osaka
In the three murder cases below, you can read the testimonies of all suspects. For each case, find who the killer is, knowing that no 2 people are in the same row or column, and that the killer was alone in a room with the victim.
SHOW EXAMPLE
Solutions
Results
| Puzzler | P1 | P2 | P3 | P4 | P5 | Total |
|---|---|---|---|---|---|---|
| Elyot G. | 0 | 1 | 0 | 1 | 1 | 3 |
| Leong W. | 0 | 1 | 0 | 0 | 0 | 1 |
| Chandan R. | 0 | 1 | 0 | 0 | 0 | 1 |
REWARDS
The TOP 3 players will win codes for some of our favorite puzzle video games. Thanks to Other Tales Interactive, Thomas Bowker, and Daniel Nora for supporting our tournament.
