T and an Island
What do the letter T and an island have in common?
SOLUTION
Both of them are in the middle of waTer.
Category: Puzzles
We do not know where this puzzle originated from. If you have any information, please let us know via email.
Thoka’s Rebus 2
Can you figure out which word is depicted by this rebus?
SOLUTION
The first image depicts a SEA. When you switch the third letter to C, you get SEC. The second image depicts RED. When you make the third letter a hard consonant, you get RET. The last two images depict a DIARY and DI (501 in Roman numerals). Therefore, you get:
SEC + RET + DIARY – DI = SECRETARY
Creepy Beasts Inc.
At Creepy Beasts Inc., three of the most dreaded animals, a tiger, a wolf, and a bear, sat in their boardroom in silence while they awaited their boss. Then, Mr. Tiger broke the silence.
“Isn’t it odd that our three surnames are the same as our three species, yet none of our surnames matches our own species?”
The wolf replied, “Yeah, but does anyone care?”
They sat in silence again…
Can you figure out the surname of each animal?
SOLUTION
Since the wolf replied to Mr. Tiger, his surname can be neither Tiger nor Wolf. Therefore, the wolf’s surname is Mr. Bear. Subsequently, Mr. Tiger must be a bear, and finally, Mr. Wolf must be a tiger.
Odd Rectangle
The sides of a rectangle have lengths which are odd numbers. The rectangle is split into smaller rectangles with sides which have integer lengths. Show that there is a small rectangle, such that all distances between its sides and the sides of the large rectangle have the same parity, i.e. they are all even or they are all odd.
SOLUTION
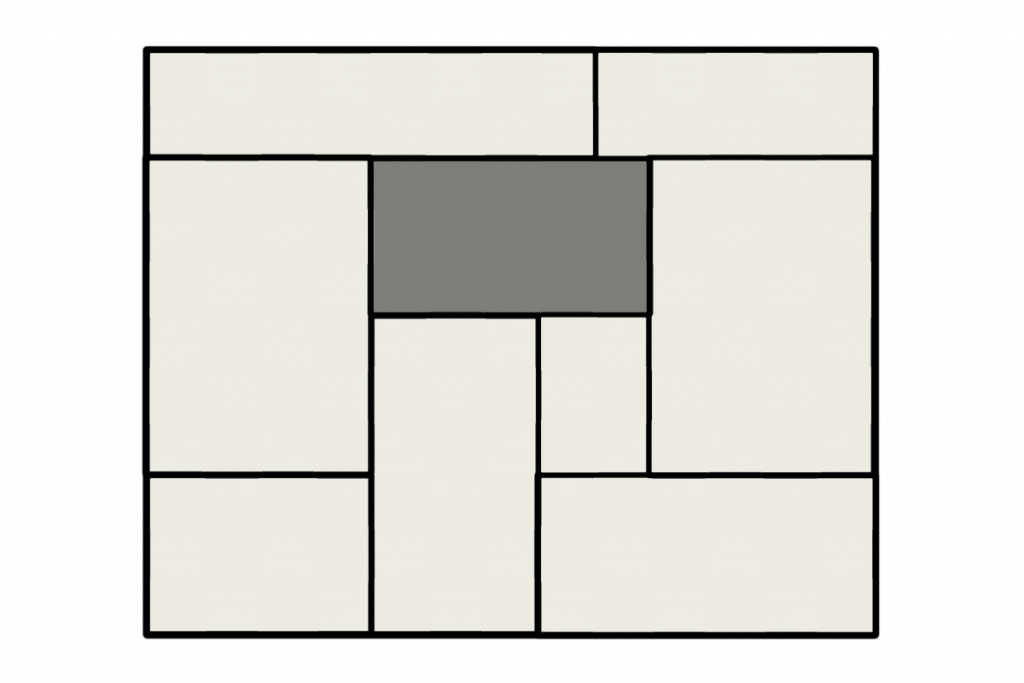
Split the large rectangle into small 1×1 squares and color it in black and white, chessboard-style, such that the four corner squares are black. Since the large rectangle has more black squares than white squares, one of the smaller rectangles also must have more black squares than white squares. Therefore, the four corners of that smaller rectangle are all black. Then, it is easy to see that all distances between its sides and the sides of the large rectangle have the same parity.
Source:
Tropical Maze
Escape from START to END in this tropical maze, created by Ben Uelk.
SOLUTION
The solution is shown below.
The Next Die
Which die completes the following sequence:
SOLUTION
If you look at dots in the top row, you will see that they are put together into groups of 1, 2, 3, 4, and so on.
Ten Lanterns
You have ten lanterns, five of which are working, and five of which are broken. You are allowed to choose any two lanterns and make a test that tells you whether there is a broken lantern among them or not. How many tests do you need until you find a lantern you know for sure is working?
Remark: If the test detects that there are broken lanterns, it does not tell you which ones and how many (one or two) they are.
SOLUTION
You need 6 tests:
(1, 2) → (3, 4) → (5, 6) → (7, 8) → (7, 9) → (8, 9)
If at least one of these tests is positive, then you have found two working lanterns.
It all of these tests are negative, then lantern #10 must be working. Indeed, since at least one lantern in each of the pairs (1, 2), (3, 4), (5, 6) is not working. Therefore, there are at least 2 working lanterns among #7, #8, #9, #10. If #10 is not working, then at least one of the pairs (7, 8), (7, 9), or (8, 9) must yield a positive test, which is a contradiction.
Buffalo Buffalo Buffalo
The sentence below is grammatically correct. Can you explain it?
Buffalo buffalo Buffalo buffalo buffalo buffalo Buffalo buffalo.
SOLUTION
The sentence says that buffalo (animals) from Buffalo (city, US), which are buffaloed (intimidated) by Buffalo (city, US) buffalo (animals), themselves buffalo (intimidate) buffalo (animals) from Buffalo (city, US).
Bridges and Crowns
I build bridges of silver and crowns of gold. Who am I?
SOLUTION
The answer is DENTIST.
Diagonal in a Rectangle
A 1000 × 1004 rectangle is split into 1 × 1 squares. How many of these squares does the main diagonal of the large rectangle pass through?
SOLUTION
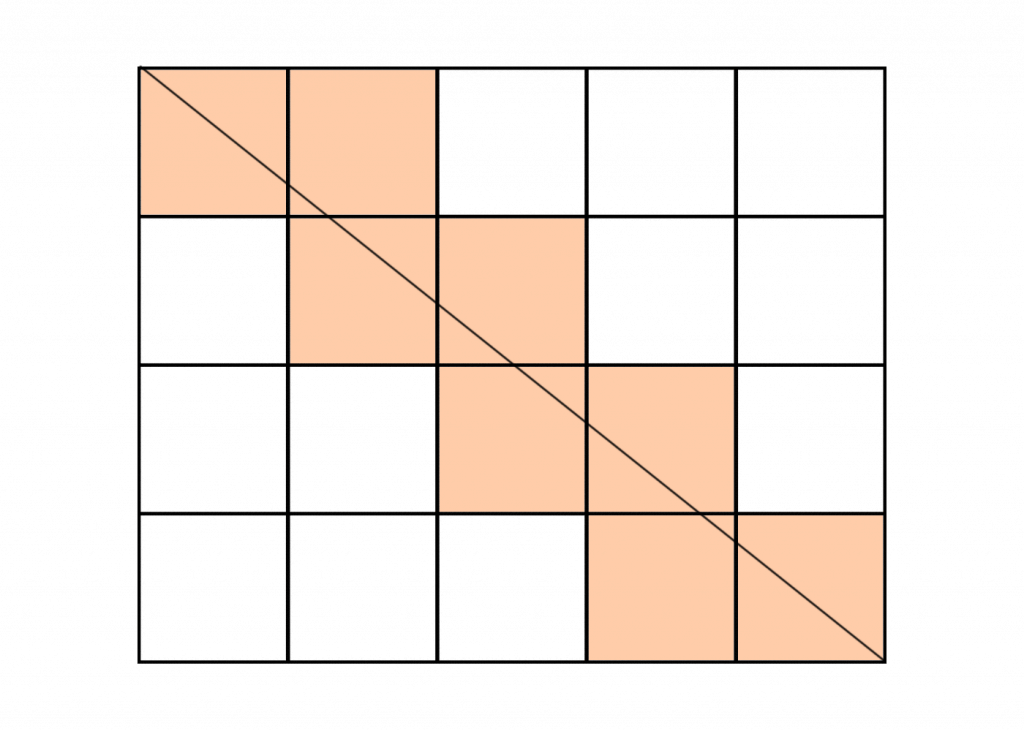
Notice that the number of small squares the main diagonal passes through is equal to the number of horizontal and vertical lines it intersects. Indeed, every time the diagonal goes through the interior of one square to the interior of another, it must intersect one of these lines.
There are 1000 + 1004 = 2004 lines which are intersected by the main diagonal. However, on four occasions (which is the greatest common divisor of 1000 and 1004), the main diagonal intersects one horizontal and one vertical line at the same time, which results in double-counting., so we must subtract 4 from the answer.
Therefore, the answer is 1000 + 1004 – 4 = 2000.