Selfmate
White starts and forces Black to mate him in 8 moves.
SOLUTION
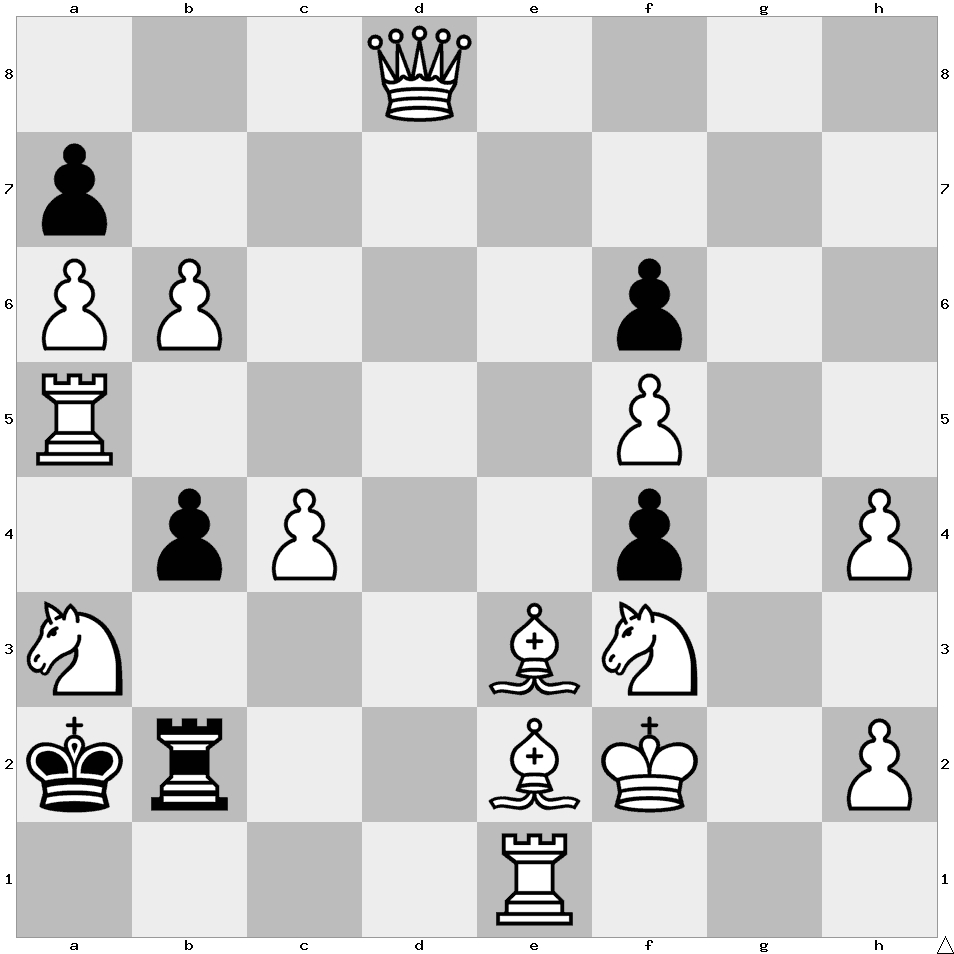
1. Nb1+ Kb3
2. Qd1+ Rc23
3. Bc1 axb6
4. Ra1 b5
5. Rh1 bxc4
6. Ke1 c3
7. Ng1 f3
8. Bf1 f2#
Category: Puzzles
We do not know where this puzzle originated from. If you have any information, please let us know via email.
WWII Planes
During World War II, the mathematician Abraham Wald was asked to help with determining which parts of the allied forces’ planes must be armored better. After examining the surviving American planes, he noticed that there were many holes in the fuselage, and very few in the engines. After careful thinking, he suggested that the armor on the engines must be improved. Why?
SOLUTION
Abraham Wald realized that the holes should have been distributed more evenly across the planes. Therefore the planes which had more holes in the fuselage survived, while the planes which had more holes in the engines got destroyed.
Dragon Maze
Find your way from the moon to the treasure, knight!
SOLUTION
The solution is shown below.
Puzzle Sum 20
What two American cities do these sums spell?
SOLUTION
SEAT + CATTLE – CAT = SEATTLE
BOY + AWL – YAWL + STONE – E = BOSTON
The Common One
Kings and queens may cling to power, and the jester’s got his call,
But, as you may all discover, the common one outranks them all.
SOLUTION
The answer is THE ACE IN A DECK OF CARDS.
Roll a Pencil
You roll a 5 sided pencil on the table. On one of its sides, it is written “HB Pencil”, the others are blank. What is the chance that the side with text on it ends up straight on top?
SOLUTION
The chance is 0%. Since the pencil has an odd number of sides, it is impossible that any of them ends up straight on top.
Divine Bell
Can you see which letters are connected with each other in this 3D maze?
SOLUTION
The solution is shown below.
Truck Too Tall
A driver needs to pass under a bridge, but his truck is one inch too tall. However, despite this issue, the driver finds a way to continue further. How?
SOLUTION
He deflated slightly the tires of the truck.
Cut the Paper
You have a sheet of paper and a rectangular piece cut from it, as shown in the picture. What is the easiest way to cut the paper into two pieces with
SOLUTION
Make a cut through the centers of the small and the big rectangle. The cut will split both the area of the big and the small (absent) rectangle by half, and therefore will do the same to their difference – the given sheet of paper.
