Category: Puzzles
Theo Guignard is a French artist, author of the book Labyrinth: Find Your Way Through 14 Magical Mazes.
Tie a Knot
First, get a completely untangled rope. Now, your task is to grab its two ends, and without letting it go, tie this knot in the middle.

In order to do this, first cross your arms, and from this position, grab the two ends of the rope. Once you untangle your arms, the knot will appear on the rope.
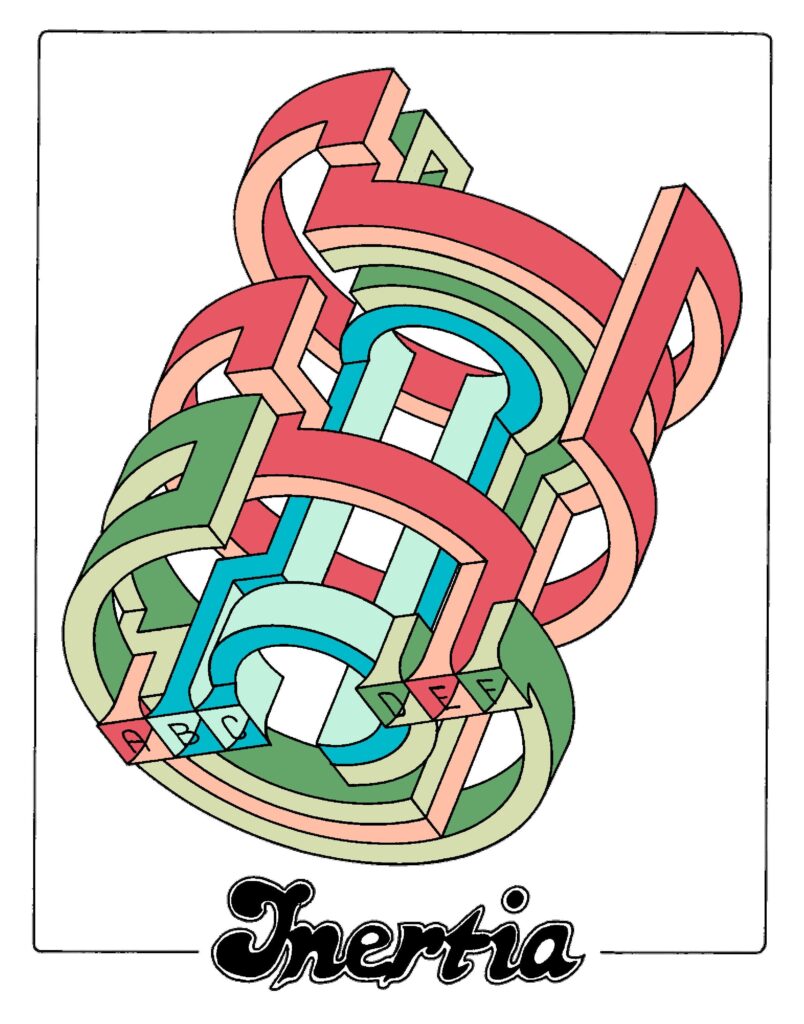
Inertia
Can you see which letters are connected with each other in this 3D maze?
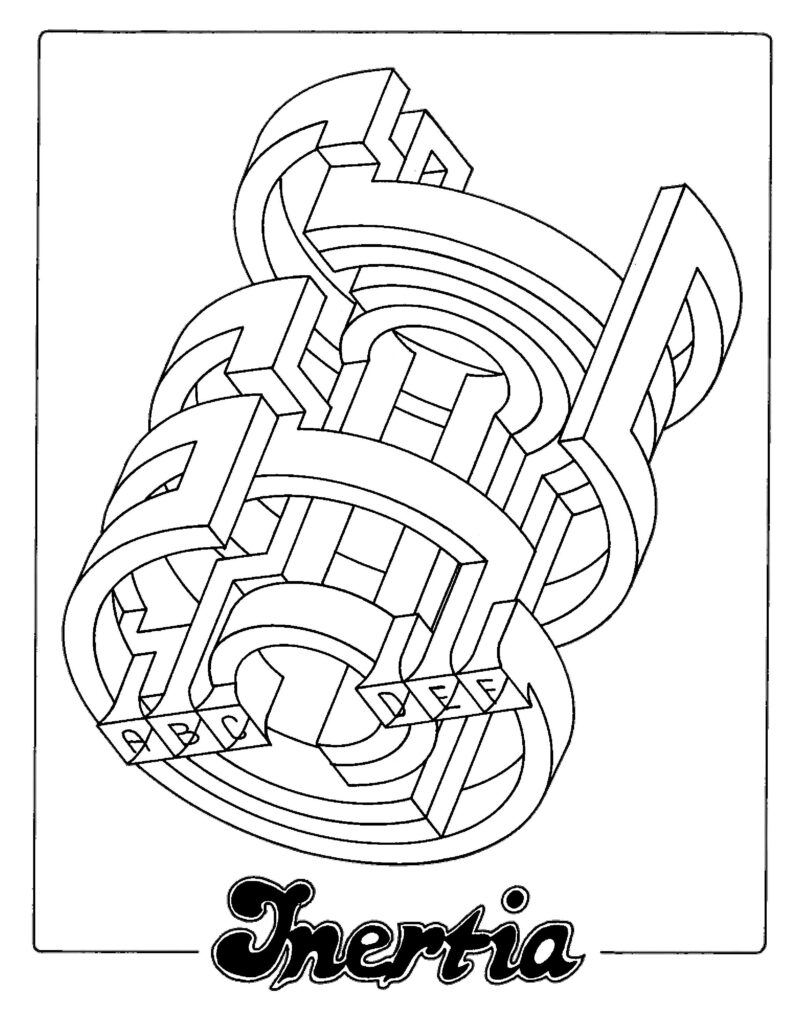
The solution is shown below.
When You Have Me
When you have me, you want to share me.
When you share me, you no longer have me.
The answer is SECRET.
Curve in a Box
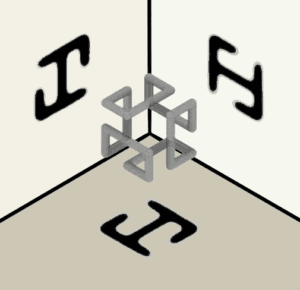
Is it possible to design a simple closed curve inside a box, such that its projections on all 6 walls of the box are trees, i.e. curves without loops?
Yes, it is possible, as shown on the image below.
Donuts and Candies
Huey has 3 donuts, Dewey has 5 donuts. Louie comes along and the three of them split the donuts equally. In exchange, Louie offers 8 candies to Huey and Dewey. What is the fair way to split the candies?
Huey must take 1 chocolate, and Dewey must take 7. This is because each of them ate 8/3 donuts, and therefore Huey gave away 1/3 of a donut, whereas Dewey gave away 7/3 of a donut.
Inside Outside
You throw away the outside and cook the inside. Then you eat the outside and throw away the inside. What do you eat?
The answer is CORN.
Puzzle Sum 16
What two animals do these sums spell?

PANTS + TRAP – STRAP + HERD + APPLE – DAPPLE = PANTHER
HIP + POP + EAR – PEAR + POTATO + EMU – TOE + SCOT – COT = HIPPOPOTAMUS
False Statements
None of these statements is correct.
At most 1 of these statements is correct.
At most 2 of these statements are correct.
…
At most 98 of these statements are correct.
At most 99 of these statements are correct.
How many of these statements are correct?
If the number of true statements is X, then statements 1, 2, … , X are wrong, and the rest are correct. Therefore X = 100 – X and X = 50. Thus, there are 50 correct statements.
Mastermind
You must find a 3-digit number. You know that:
- 682 shares one digit with the number, and it is well placed;
- 614 shares one digit with the number, but it is wrongly placed;
- 296 shares two digits with the number, but they are wrongly placed.
What is the number?
The first and second clues imply that the 6 is not a part of the number. The third clue then implies that 2 and 9 are parts of the number. Now the first clue implies that 2 is the last digit of the number, and the third clue implies that 9 is the first digit of the number. Finally, the second clue implies that 4 is the second digit of the number. Therefore, the number is 942.