Not a Nickel
I have two coins, worth 55 cents in total. If one of them is not a nickel, what are the coins?
One of them is not a nickel, but the other one is. The two coins are a 50 cents and a nickel.
We do not know where this puzzle originated from. If you have any information, please let us know via email.
I have two coins, worth 55 cents in total. If one of them is not a nickel, what are the coins?
One of them is not a nickel, but the other one is. The two coins are a 50 cents and a nickel.
In one house deep in the forest
The seventh dwarf is also playing chess; 2 people are needed for this.
There are 2 wizards and each of them has infinitely many hats on his head. Every hat has 50-50 chance to be white or black, and the wizards can see the hats of the other person, but not their own. Each wizard is asked to identify a black hat on his head without looking, and they win if both succeed to guess correctly. If the wizards are allowed to devise a strategy in advance, can they increase their chance of winning to more than 25%?
Each wizard guesses the position of the lowest black hat on the head of the other wizard. Then the chance of winning becomes 1/4 + 1/16 + 1/64 + … = 1/3. It can be shown that this is an optimal strategy as well.
Last week we found out that Puzzle Pranks Co. have invented a new type of puzzle – Rubik’s Chess. The goal is simple – you get a scrambled cube with various chess pieces on its sides, and you must unscramble it so that on each side there is one mated King, assuming the kings
We are usually good with this type of puzzles, but we spent our entire weekend trying to solve this one without any success. We even started wondering if it can be actually solved, so decided to share it with you and see if you can help us figure that out.
Below you can see the way the cube looks when seen from 8 different angles:
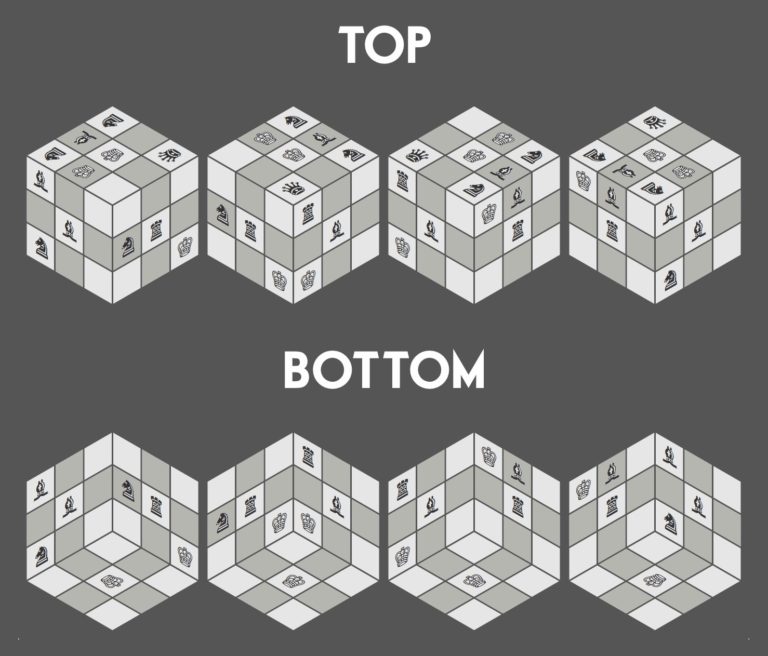
Remark: The orientations of the pieces are irrelevant to the final solution, i.e. they don’t need to be consistent on each side.
The Rubik’s Chess puzzle cannot be solved. You can see a detailed solution HERE.
There are 10 birds on a tree. One hunter shoots at them and hits 2. How many birds are left on the tree?
Zero – the remaining 8 birds get scared and fly away.
Between every pair of major cities in Russia, there is a fixed travel cost for going from either city to the other. Traveling salesman Alexei Frugal starts in Moscow and visits all cities exactly once, choosing every time the cheaper flight to a city he has not visited so far. Salesman Boris Lavish starts in St Petersburg and visits all cities exactly once, choosing every time the most expensive flight to a city he has not visited so far. Can Alexei end up spending more money than Boris after they end their journeys?
No, it is impossible. For every trip of Alexei we will choose a trip of Boris, which costs at least as much.
Let the number of cities is n and Alexei visits them in order 1 -> 2 -> … -> n.
If Boris visits city n-1 before city n, then pair Alexei’s trip (n-1, n) with Boris’ trip (n-1, #). Notice that C(n-1, n) < C(n-1, #).
If Boris also visits city n-2 before city n, then pair Alexei’s trip (n-2, n-1) with Boris’ trip (n-2, #). Notice that C(n-2, n-1) < C(n-2, n) < C(n-2, #).
Continue like this until get to a city k which Boris visits after city n. Then pair Alexei’s trip (k, k+1) with Boris’ trip (n, #). Notice that C(k, k+1) < C(k, n) < C(n, #).
Next, check whether Boris visits city k – 1 before city k, and pair Alexei’s trip (k-1, k) with either (k-1, #) or (k, #). Continue like this, until pair all of Alexei trips with more expensive Boris trips.
What gets wetter as it dries?
The answer is TOWEL.
Starting from this position, can you make 39 consecutive checks – 20 from White and 19 from Black?
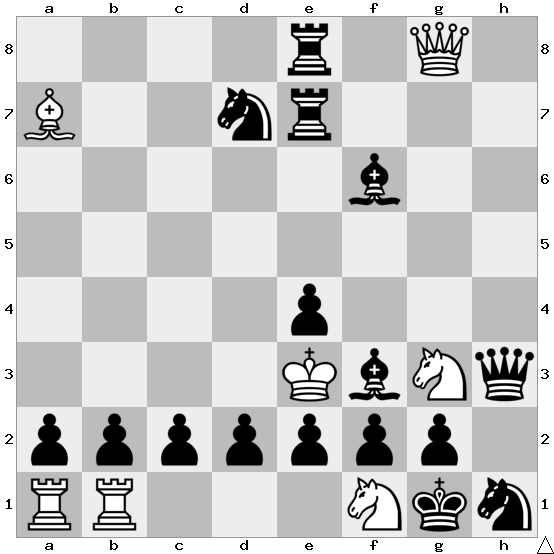
The sequence is as follows:
1. Nh2+ f1N+
2. Rxf1+ gxf1N+
3. Ngxf1+ Bg5+
4. Qxg5+ Bg2+
5. Nf3+ exf3+
6. Kd3+ Nc5+
7. Qxc5+ Re3+
8. Nxe3+ c1N+
9. Qxc1+ d1Q+
10. Qxd1+ e1N+
11. Qxe1+ Bf1+
12. Nxf1+ f2+
13. Ne3+ f1Q+
14. Qxf1+ Qxf1+
15. Nxf1+ Re3+
16. Nxe3+ b1Q+
17. Rxb1+ axb1Q+
18. Nc2+ Nf2+
19. Bxf2+
What animal does this sum spell?

MARSH + ARK – SHARK + TEN = MARTEN
Please confirm you want to block this member.
You will no longer be able to:
Please allow a few minutes for this process to complete.