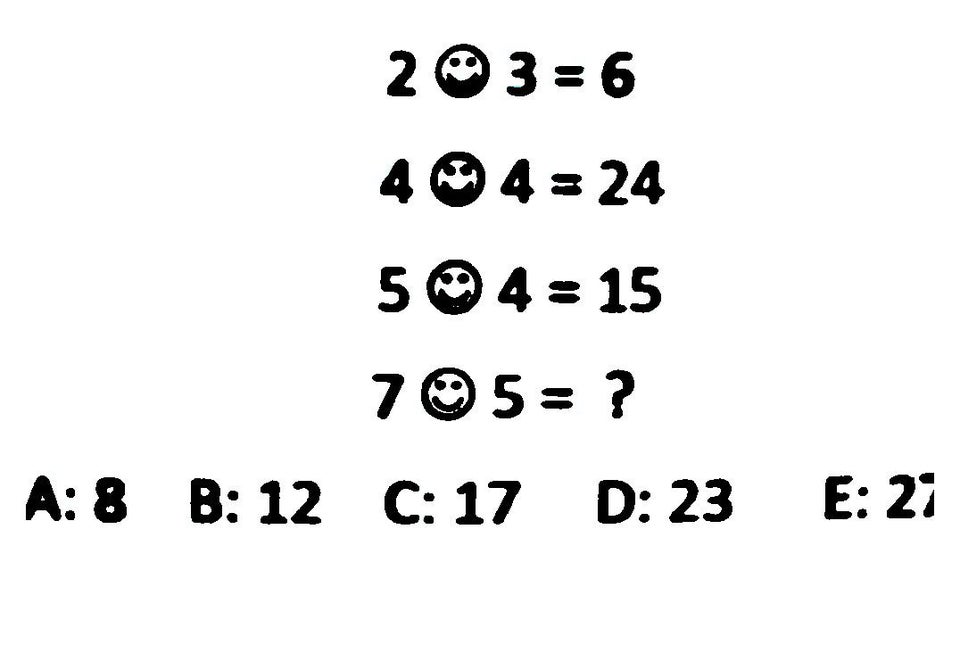Man Without a Moustache
Can you find the man without a moustache?
Archives: Community Posts
Puzzle Prime is tirelessly looking all around the internet to find the very best puzzles and bring them all to puzzleprime.com.
Calculus
Suppose f(x) is the non decreasing function such that f(x)>0 , for all x.
Prove that there exists x, such that f(x+1/f(x))<2f(x).
This is interesting and challenging…
Divisor puzzle
Here’s an interesting puzzle that you can do with a pack of cards. Start with the cards 1, 2, …, N, where N is some whole number. If you’re doing this with cards, then you might count the Jack as 11, the Queen as 12, King as 13. Let’s say, for purposes of this example, that N=5, so you start with the Ace, 2, 3, 4 and 5 of diamonds (Ace being 1). The aim of the puzzle is to play all the cards to the table obeying the following rules:
1. The first card played must be the highest card, the 5 of diamonds in this case.
2. Subsequent cards can only be played if they are a divisor of the cumulative total of the cards currently on the table. A divisor is a smaller number that evenly divides a larger number.
In the present example, a valid sequence of plays would be 5 (5), A (6), 2 (8), 4 (12), 3 (15), where I’ve put the cumulative total in brackets afterwards.
It gets progressively harder as N gets larger. Also, for N>13 you tend to run out of cards, so you have to do it in your head! I got up to N=23. How high can you go? Maybe post your solutions below so that we can compare.
Selfies
Annie took selfies with her friends. Each of 8 friends appeared in two or three photos. There are five friends and Annie in each photo. How many selfies have Annie taken?
When Worlds Collide
I thought of this problem many years ago but I’ve never been able to come up with a solution, although I feel there ought to be one. Maybe you folks would be interested in giving it a try. It goes like this:
In the 1951 movie When Worlds Collide (as I remember it), a large team works frantically to build a spaceship to escape the Earth before it’s destroyed. When someone realizes that there are more people building the ship than it can carry, it’s decided that a lottery will be held and the winners announced on launch day. When that day comes and the list of winners is posted, a young man finds his name on the list and runs to tell his girlfriend, but when he finds her she’s crying because, tragically, her name isn’t on the list.
The puzzle is this: How could a lottery be held that would avoid situations like that? Can you devise a set of lottery rules that would allow couples, or perhaps even larger groups, to specify in advance that either all of the group or none of the group win, while maintaining exactly the same probability of winning for each individual person, including those who choose not to pair up with anyone?
