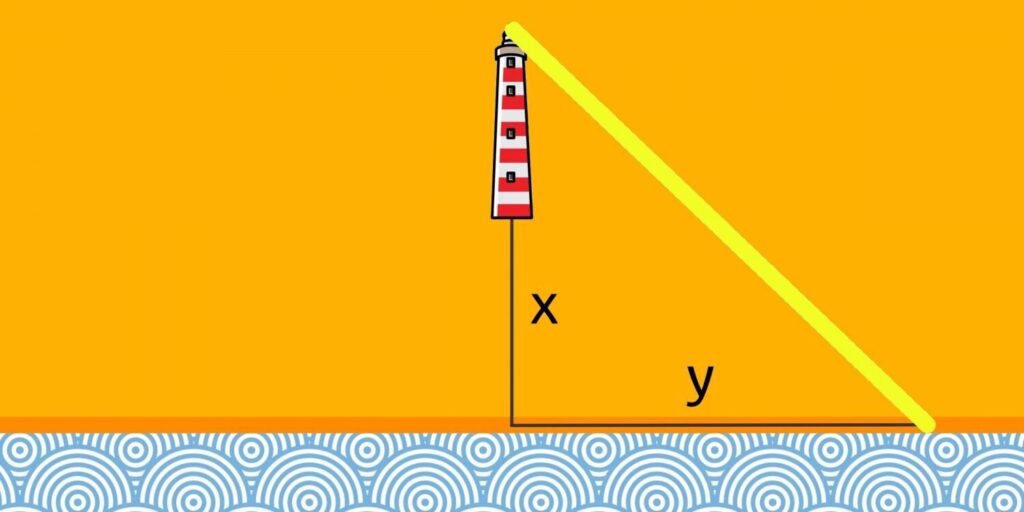
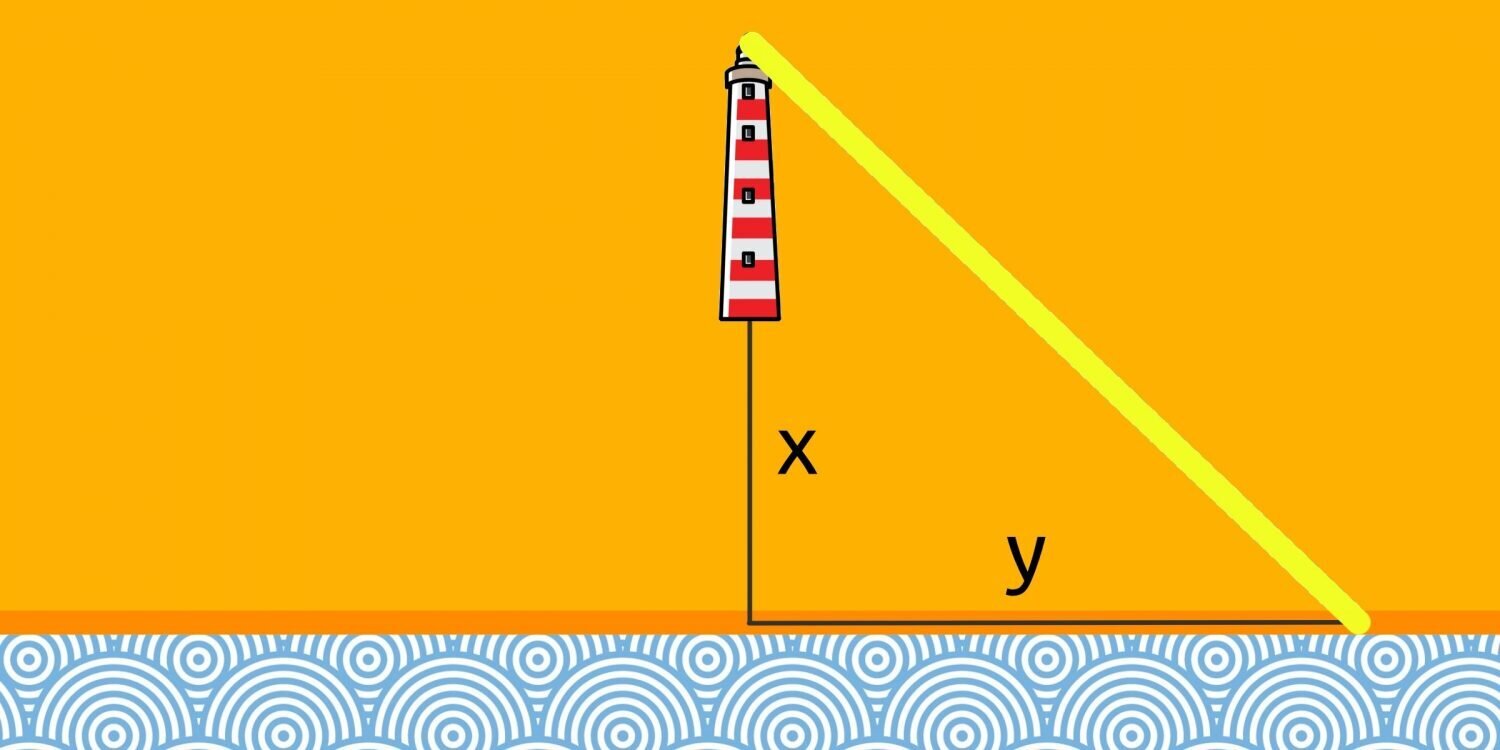
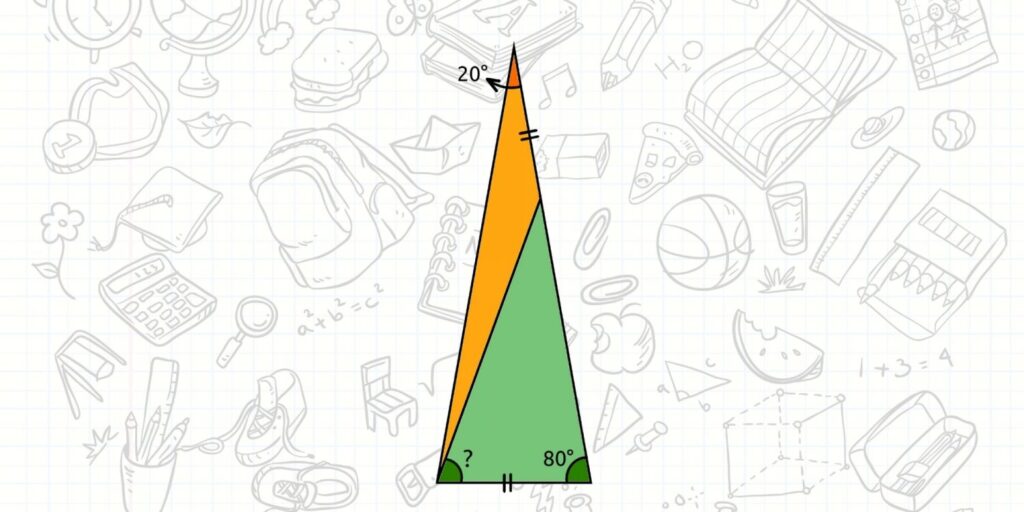
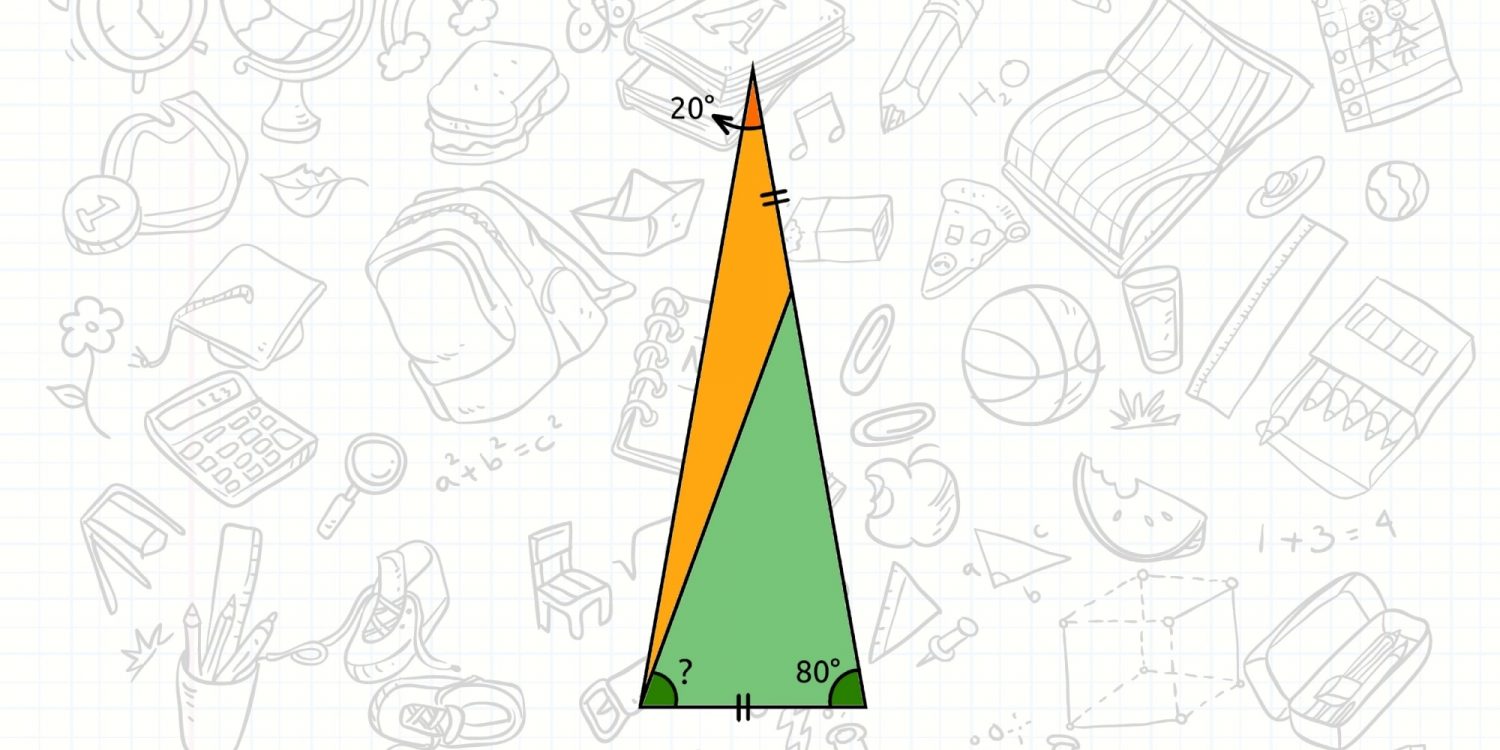
Community Category: Math

Find all positive integers (n) such that n/d(n) is the prime number, Where d(n) is the number of divisors of n. For example, d(15)=4 {1,3,5,15}.

Suppose f(x) is the non decreasing function such that f(x)>0 , for all x.

Prove that there exists x, such that f(x+1/f(x))<2f(x).

This is interesting and challenging…

Annie took selfies with her friends. Each of 8 friends appeared in two or three photos. There are five friends and Annie in each photo. How many selfies have Annie taken?

I thought of this problem many years ago but I’ve never been able to come up with a solution, although I feel there ought to be one. Maybe you folks would be interested in giving it a try. It goes like this:

In the 1951 movie When Worlds Collide (as I remember it), a large team works frantically to build a spaceship to escape the Earth before it’s destroyed. When someone realizes that there are more people building the ship than it can carry, it’s decided that a lottery will be held and the winners announced on launch day. When that day comes and the list of winners is posted, a young man finds his name on the list and runs to tell his girlfriend, but when he finds her she’s crying because, tragically, her name isn’t on the list.

The puzzle is this: How could a lottery be held that would avoid situations like that? Can you devise a set of lottery rules that would allow couples, or perhaps even larger groups, to specify in advance that either all of the group or none of the group win, while maintaining exactly the same probability of winning for each individual person, including those who choose not to pair up with anyone?

What is the number of non-strictly increasing sequences of M integer numbers between 1 and N?

Does the function f(x) = 1 + x¹/1! + x²/2! + x³/3! + … + xⁿ/n! have any real roots?

You start with $20 and keep betting $1. What is the probability that you will get broke before you win $50? What is the expected number of bets until one of these 2 events happens?

100 real random numbers between 0 and 1 are written in a row. What is the expected number of local minima in the row, i.e. numbers which do not stand next to a smaller number?