Puzzles about Arranging Numbers on Edges of Directed Graphs
Hi,
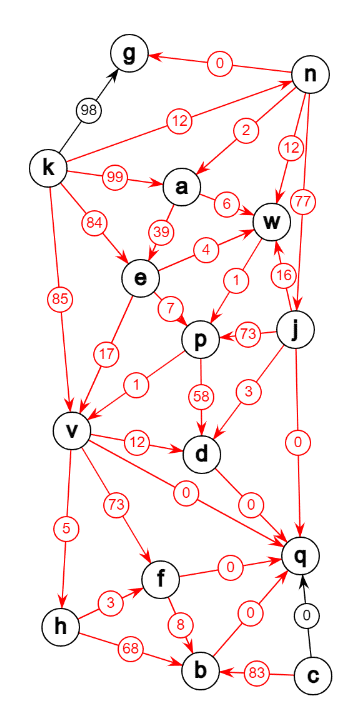
Here’s a puzzle about arranging numbers on arrows of a directed graph so that numbers on all arrows entering each node are (strictly) less than numbers on all arrows leaving that node.
To shuffle numbers between two arrows, you click on the number on one arrow and then you click on the number of the other arrow.
Here’s the link: https://game-space.org/15nodes-33arrows-puzzle2-f/
You can also find many more of those puzzles here: https://game-space.org/category/solve-puzzles/