Airplane on a Conveyor Belt
A Boeing 747 is sitting on a conveyor belt, as wide and long as a runway. The conveyor belt is designed to exactly match the speed of the wheels, moving in the opposite direction. Will the plane take off?
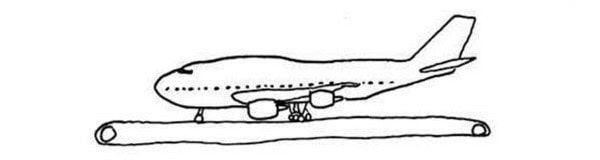
We do not know where this puzzle originated from. If you have any information, please let us know via email.
A Boeing 747 is sitting on a conveyor belt, as wide and long as a runway. The conveyor belt is designed to exactly match the speed of the wheels, moving in the opposite direction. Will the plane take off?

A teacher in English had asked James and John to describe a man who had suffered from a cold in the past. James while John had had had had had had had had had had had a better effect on the teacher.
Add punctuation to the sentence in bold, so that it makes sense.
Cut out the black shape and then fold it perfectly into a cube, without overlapping.
Three friends, A, B and C, want to find out what their average salary is without disclosing their own salaries to the others. How can they do it using only verbal communication?
What is the minimum number of folds you need in order to create a 3-inch measurement from an 8.5×11 inches paper?
Nine pirates have captured a treasure chest. In order to protect it, they decide to lock it using multiple locks and distribute several keys for each of these locks among them, so that the chest can be opened only by a majority of the pirates. What is the minimum number of keys each of the pirates should get?
A hundred fish are swimming along a stream at different velocities. If one fish catches up to another fish, it eats it and continues swimming. What is the expected number of fish that will survive?
Bobby and Garry are playing chess. If Garry is playing with the black figures and agrees to mirror every move Bobby makes, what is the minimum number of moves in which Bobby can mate his opponent?

A man decides to climb a mountain. He starts at sunrise from the bottom of the mountain and arrives at the top at sunset. He sleeps there and on the next day he goes back the same way, descending at higher speed. Prove that there is some point of his path, on which the man will be at the same time on both days.
Please confirm you want to block this member.
You will no longer be able to:
Please allow a few minutes for this process to complete.
Notifications