Going Back Home
A man leaves home and makes three left turns, only to return home facing two men wearing masks. Who are those two men?
SOLUTION
The person is a baseball player. The men are a catcher and an umpire.
Difficulty: Advanced
We do not know where this puzzle originated from. If you have any information, please let us know via email.
Crowns and Lions
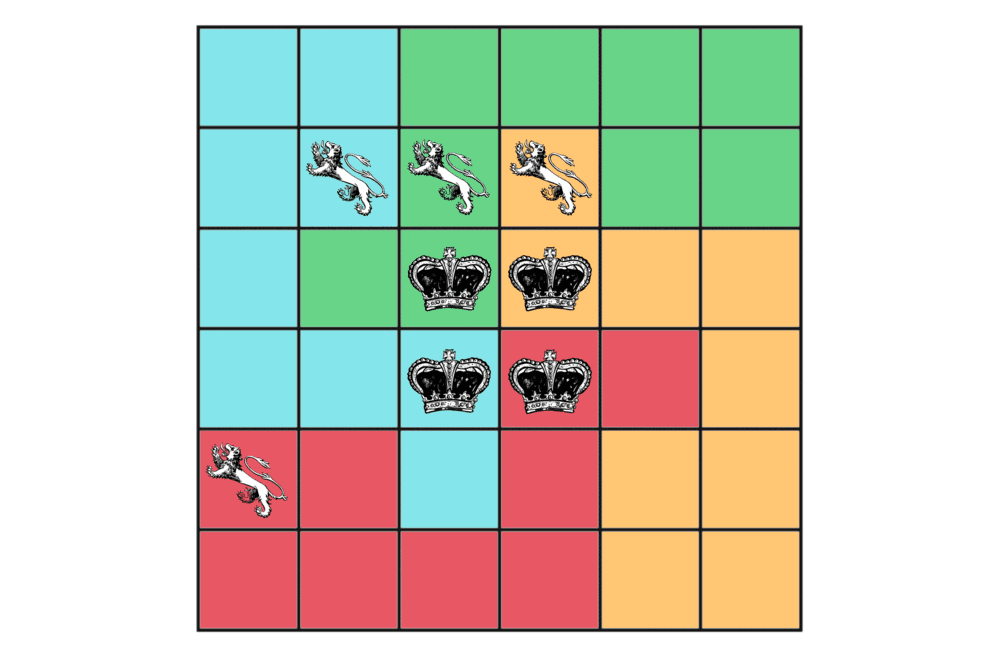
Split the grid into four identical regions, such that each region contains a lion and a crown.
SOLUTION
The solution is shown below.
One to One Hundred
99 unique numbers between 1 and 100 are listed one by one, with 5 seconds pause between every two consecutive numbers. If you are not allowed to take any notes, what is the best way to figure out which is the missing number?
SOLUTION
Keep up adding the given numbers and remember only the last two digits of the sum. In the end, if the result is less than 50, subtract it from 50. If the result is larger than 50, subtract it from 150. This method works because the sum of all numbers from 1 to 100 is 5050, so if you know the sum of all the listed numbers, you will know the missing number as well.
Two Lost Cards in a Deck
Below you can read the steps of a magic trick, as well as a video of its live performance. Your goal is to figure out how the trick is done, then perform it for your friends and challenge them to figure out the trick themselves.
- Take out from your pocket a deck of cards, which is visibly shuffled.
- Ask your first assistant to cut the deck, then take the top card from the bottom pile of cards and memorize it.
- Ask your second assistant to take the next card from the bottom pile and memorize it.
- Ask your first assistant to return his card back on the top of the bottom pile, then ask your second assistant to do the same.
- Place the two piles of cards on top of each other and cut the deck multiple times.
- Split the deck into two piles of cards, dealing consecutively one card on the left, then one card on the right, and so on, until you run out of cards.
- Take one of the two piles of cards, look at it, and guess correctly what cards were chosen by your assistants.
How does the magic trick work? Below you can see a live performance of the magic trick from Penn and Teller’s show Fool Us.
SOLUTION
The secret of the trick is to memorize the group of cards which are located in even positions and the group of cards which are located in odd positions in the original deck. An easy way for doing this is to split the cards into two groups, such that the cards in the first group are only spades and diamonds, and the cards in the second group are only clubs and hearts.
When the two assistants pick their cards and then return them back into the deck, the order of the cards is reversed. When you split the original deck into two piles (even after cutting it several times), each of the piles will contain a card which should not be there. For example, the group of spades and diamonds will contain one clubs card, and the group of clubs and hearts will contain one diamonds card. These two cards are the ones which were picked by the assistants.
A Beetle and Four Spiders
A beetle is located in the center of a square carpet. The edges of the carpet are colored in red, green, blue, and yellow. Four spiders of the same colors are on the carpet’s corners. Each spider can only move on the edge with its matching color. Can the beetle escape the carpet and flee without encountering the spiders if it is 1.5 times slower than them?
SOLUTION
No, the spiders will always be able to contain the beetle within the carpet. We draw two perpendicular lines passing through the beetle which are parallel to the diagonals of the square. The spiders’ strategy is to follow the four points where these lines intersect with the boundary of the square. When a spider’s corresponding intersection point moves to an edge of a different color, the spider waits in the corner. In order to accomplish this strategy, the speeds of the spiders need to be at least √2~1.4 times higher than the speed of the beetle.
Programmers and Coins
One programmer draws on a sheet of paper several circles in a line, representing coins, and puts his thumb on the first circle, covering the rest with his hand. Then he asks another programmer to guess how many different head-tail combinations are possible if someone flips all the (imaginary) coins on the paper. The second programmer, without knowing the number of circles, takes the pen and writes down a number. Then the first programmer lifts his hand and sees that the correct answer is written on the paper. How did the second programmer manage to do this?
SOLUTION
The second programmer wrote down “1” in front of the first circle. When the second programmer lifted his hand, he saw the number “10…00”, which is exactly the number of possible head-tail combinations in binary system.
Unusual Position
What is the smallest number of moves needed to result in this unusual position?
SOLUTION
The shortest game takes just 4 moves:
1. Nf3 e5
2. Nxe5 Ne7
3. Nxd7 Nec6
4. Nxb8 Nxb8
Pass Through a Card
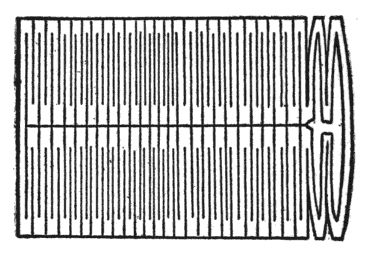
Take a small piece of paper – 4in by 6in, and scissors. Can you cut the paper in such a way, so that you can pass through it
SOLUTION
Yes, you can, as shown on the image below.
Be brave!
Which is the best move for White in this position?
SOLUTION
The best move is 1. Rc8+. Then either 1. … Kxb7 2. Rxd8, or 1. … Rxc8 2. Qxa7 Kxa7 3. bxc8 = N+, and Black loses both the Rook and the Queen.
Non-Transitive Dice
This is a non-transitive dice set, i.e. every dice in it is weaker than some other dice. Can you design a non-transitive set with only 3 dice?
Remark: “Weaker” means that it loses more often than it wins.
SOLUTION
The simplest solution is given by:
2, 2, 4, 4, 9, 9;
1, 1, 6, 6, 8, 8;
3, 3, 5, 5, 7, 7.
Another solution is given by the so-called “Miwin’s dice”. They are as follows:
1, 1, 3, 5, 5, 6;
2, 3, 3, 4, 4, 5;
1, 2, 2, 4, 6, 6.