0 > 2, 2 > 5, 5 > 0
0 > 2, 2 > 5, 5 > 0. What is this?
SOLUTION
This is the game “Rock, Paper, Scissors”. Rock (0 fingers) beats scissors (2 fingers). Scissors (2 fingers) beats paper (5 fingers). Paper (5 fingers) beats rock (0 fingers).
Difficulty: Advanced
We do not know where this puzzle originated from. If you have any information, please let us know via email.
Seven Sevens
Seven sevens are given. Find the other digits in this multiplication.
SOLUTION
The answer is:
21817 x 96787 = 2111601979
Pac-Men Maze
Find a path between the two Pacmen in this double-sided maze. You can not switch between the top and the bottom sides of the path you are traversing.
SOLUTION
The solution is shown below.
Mystery Mate
White plays and mates Black in one move. However, there is a mystery in this position that has to be revealed first.
SOLUTION
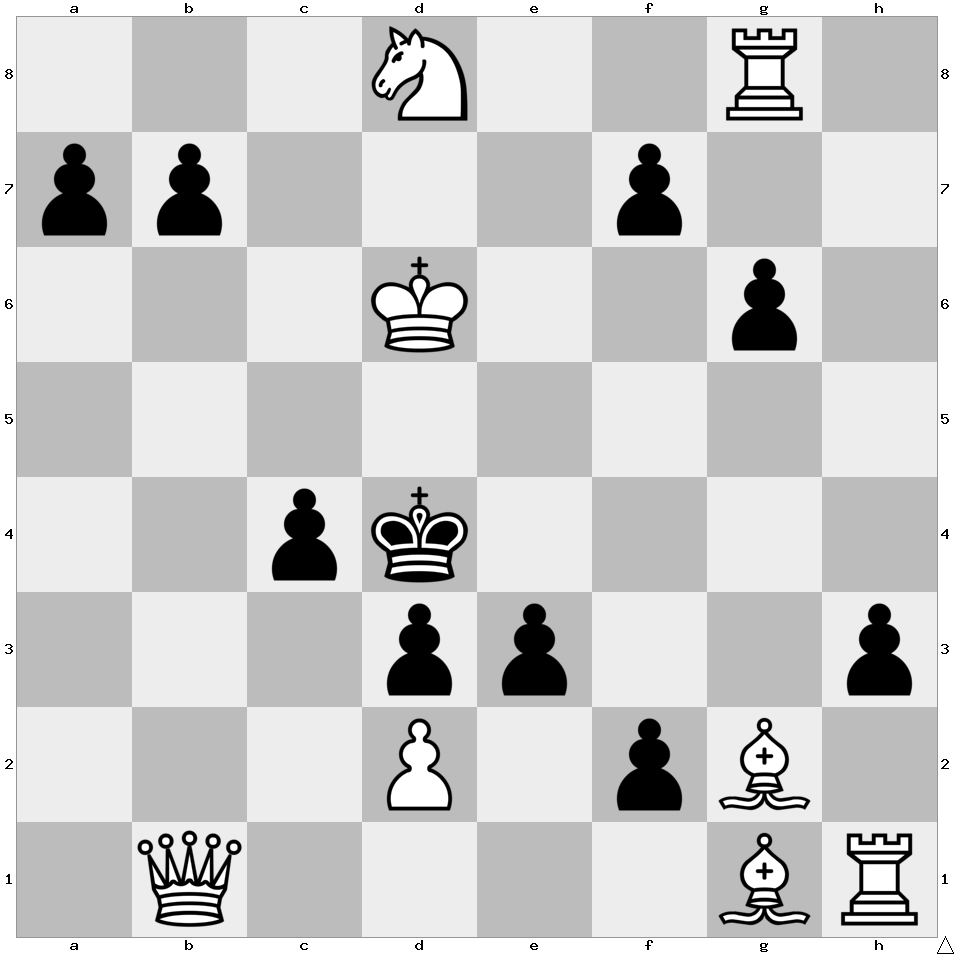
The mystery is that someone has just placed one extra black pawn on the board – there are 9 in total. Also, no matter which one is the added pawn, there always exists a mate in one move.
If the extra pawn was a7 – Qb6
If the extra pawn was b7 – Kc6
If the extra pawn was c4 – Qb4
If the extra pawn was d3 – Qe4
If the extra pawn was e3 – Bxf2
If the extra pawn was f7 – Ke6
If the extra pawn was g6 – Rg4
If the extra pawn was h3 – Rh4
FEATURED
Repetitive
You have two groups of words:
- black, word, English, brief, noun, grandiloquent, last
- white, number, Russian, long, verb, unpretentious, first
To which group does “repetitive” belong?
SOLUTION
The first group contains self-explanatory words (known as autologicals), the second group does not. Therefore “repetitive” should belong to the first group.
Four Points in the Plane
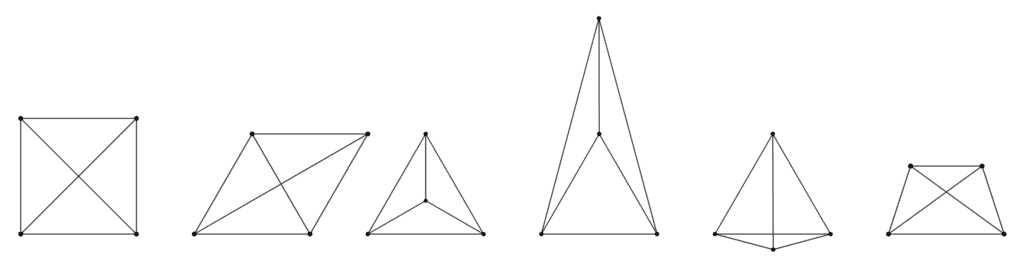
Find all configurations of four points in the plane, such that the pairwise distances between the points take at most two different values.
SOLUTION
All 6 configurations are shown below: a square, a rhombus with 60°-120°-60°-120°, an equilateral triangle with its center, an isosceles triangle with 75°-75°-30° and its center, a quadrilateral with 75°-150°-75°-150°, and a trapezoid with base angles of 72°.
Twiddled Bolts
Two identical bolts are placed together so their grooves intermesh. If you move the bolts around each other as you would twiddle your thumbs, holding each bolt firmly by the head so it does not rotate and twiddling them in the direction shown below, will the heads:
(a) move inward
(b) move outward, or
(c) remain the same distance from each other?
SOLUTION
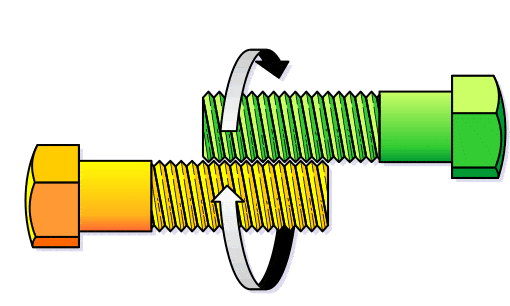
One of the bolts will be screwing itself, and the other one will be unscrewing itself. This will happen at the same pace and the bolts will remain the same distance from each other. Thus the answer is (c).
Driver’s Seat
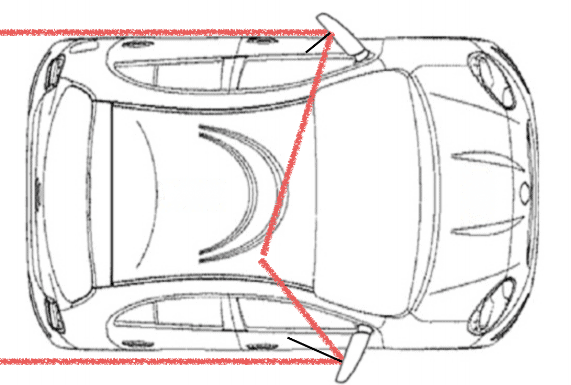
Where is the driver sitting in this car?
SOLUTION
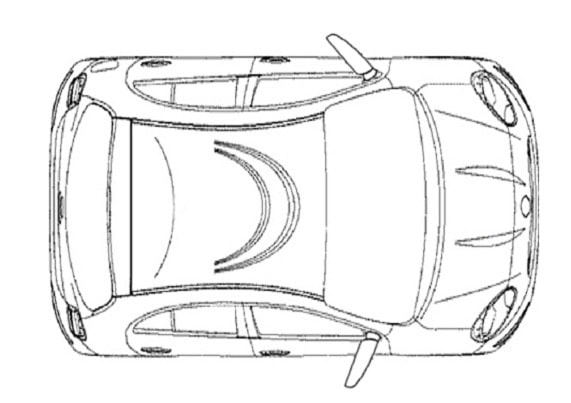
Using the positioning of the mirrors, you can conclude that the driver is sitting on the right.
Lab Mice
A scientist has 9 bottles, exactly one of which contains poison. The poison kills any creature which drinks it within 24 hours. If the scientist has 2 lab mice at his disposal, how can he find which is the poisonous bottle within 2 days only?
SOLUTION
Label the bottles B1, B2, B3, … , B9.
The first day he lets the first mouse drink B1, B2, B3, and let the second mouse drink B1, B4, and B5. If after 24 hours both mice die, then the poisonous bottle is B1. If only one mouse dies, say the first one, then he lets the second mouse drink B2. If it dies, then the poisonous bottle is B2, otherwise, it is B3. Finally, if neither mouse dies, then he lets the first mouse drink B6 and B7, and lets the second mouse drink B6 and B8. If both mice die after 24 hours, then the poisonous bottle is B6. If only one mouse dies, say the first one, then the poisonous bottle is B7. If neither mouse dies, then the poisonous bottle is B9.
FEATURED
Parking Lot
On top of which number is the car parked?
SOLUTION
You are looking at the parking lot upside-down. The numbers on the picture are from 85 to 92. The car is parked on top of 87.