Nine Fifty
Move the minus sign to make an expression equivalent to nine fifty.
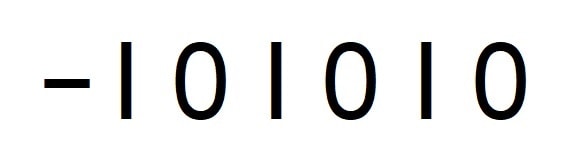
Move the minus sign to the top of the second vertical line to get “10 to 10”, i.e. 9:50.
Mel Stover (1912-1999) is a Canadian magician who has created numerous puzzles, optical illusions, and mind games.
Move the minus sign to make an expression equivalent to nine fifty.
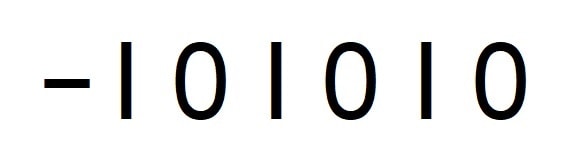
Move the minus sign to the top of the second vertical line to get “10 to 10”, i.e. 9:50.
What are the names of the three girls in this rock band?
T _ _ _ _ & D _ _ _ _ _ _ & L _ _ _

The vocalist’s name is Tessa. On her notebook it is written “I’m diving into the DARK gloom End to start“. On the poster in the top right corner it is written DARK and underneath ASSET. “Asset” spelled backwards becomes TESSA.
The bassist’s name is Delilah. Her shirt features a cat, which is also present on the Freddy Mercury poster. The lyrics written on it are from the song “Delilah” by Queen.
The drummer’s name is Lisa. Inside her backpack there is a copy of the book “1984” by G. Orwell. On her backpack there is a sticker which also appears on the poster behind Delilah. The poster says “Local punk’o’matIc AnarchiSts bazAr”. If one selects the 1st, the 9th, the 8th, and the 4th letters from each word, the resulting name is LISA.
We have written the numbers from 1 to 12 on the faces of a regular dodecahedron. Then, we have written on each vertex the sum of the five numbers on the faces incident with it. Is it possible that 16 of these 20 sums are the same?
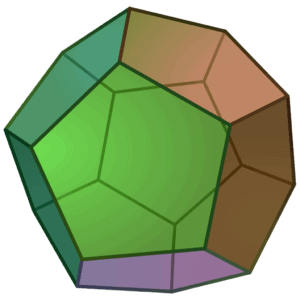
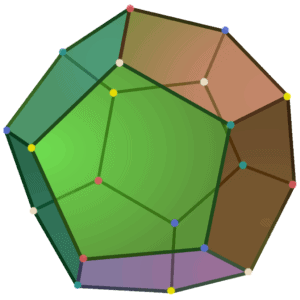
We color the vertices in five colors as shown in the image below, such that each face of the dodecahedron has 1 vertex of each color. Then, the sum of the four numbers from each color must be equal to the sum of all numbers written on the faces: 1 + 2 + … + 12 = 78.
If 16 of the vertices have the same number written on them, then by the pigeonhole principle there will be 4 vertices with identical colors and identical numbers. Since 78 is not divisible by 4, we conclude that this is impossible.
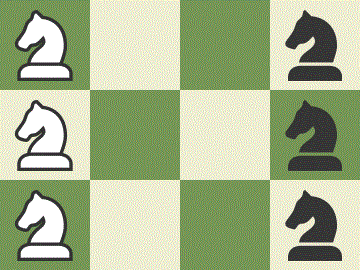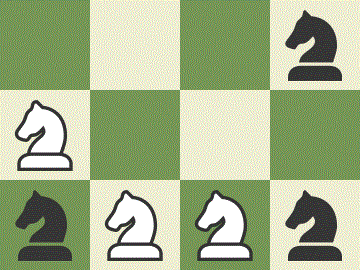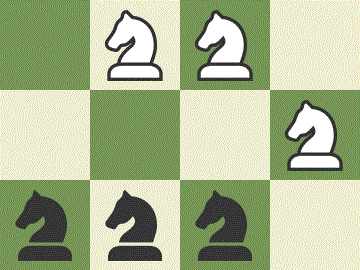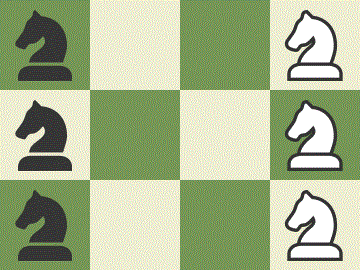
Your goal is to switch the positions of the three white knights with the positions of the three black knights. What is the least number of moves required to do this?

The least number of moves required to switch the positions of the knights is 16. An example is shown below.
Next, we prove that it is impossible to switch the positions of the knights with less than 16 moves. Since the white knights occupy 2 black and 1 white squares, they need to end up on 2 white and 1 black squares, and each knight must make at least 2 moves in order to get to the opposite side, the total number of moves for the white knights should be an odd number, larger or equal to 2+2+2=6. The same applies to the total number of moves for the black knights. Therefore, the only possible way to get a total number of moves less than 16 is if both the white knights and the black knights move exactly 7 times.
We assume it is possible to switch the positions with 7+7=14 moves in total. Then, the white knight on A2 and one of the white knights on A1, A3 should make 2 moves each, and the third white knight should make 3 moves and land on a white square, either D1 or D3. Without loss of generality, we assume the knight on A1 makes 3 moves: A1-B3-C1-D3. Then, the knight on A2 should make 2 moves: A2-C3-D1, and the knight on A3 should make 2 moves: A3-B1-D2.
We make the same argument for the black knights. Since it is impossible that the white knight on A1 moves along the trajectory A1-B3-C1-D3 and also the black knight on D3 moves along the trajectory D3-C1-B3-A1, we conclude that the black knight on D1 should make 3 moves: D1-C3-B1-A3, the black knight on D2 should make 2 moves: D2-B3-A1, and the black knight on D3 should make 2 moves: D3-C1-A2.
This is only possible if:
We get a contradiction which means that the least number of moves is 16.
Recognize the phrases depicted by the “terrible rebuses” below.

Fill the three missing numbers (using words) in the shoe below.
Remark: The missing words can be of any length.

You should fill the words FIVE, THREE, FOUR to get:
“In this shoe, there are five H’s, three O’s, and four T’s.”
You are chasing a criminal riding a bicycle, and you find his tracks left in the dirt. By investigating the tracks, can you determine which direction the criminal has fled to: left or right?

The front wheels of the bicycle are traveling more distance and making sharper turns. Thus, the red tracks (as shown on the image below) correspond to the front wheel, and the green tracks correspond to the back wheel.

Then, since the back wheel is always pointing towards the front wheel, we conclude that the bicycle is moving towards the right.

Recognize the phrases depicted by the “terrible rebuses” below.

Find 27 figures of speech in the illustration by Ella Baron below.

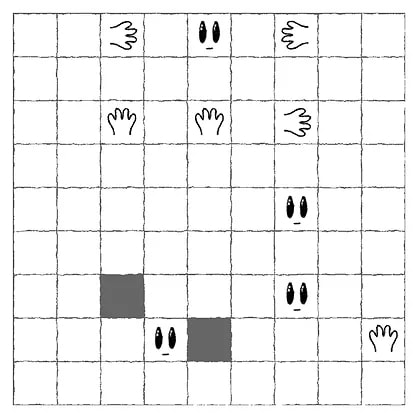
Partition the grid into disjoint “creatures”, according to the following rules:
Examine the first example, then solve the other three puzzles.
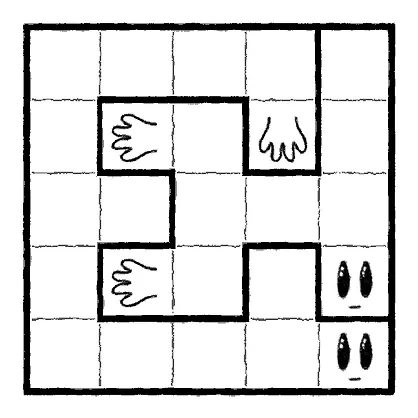

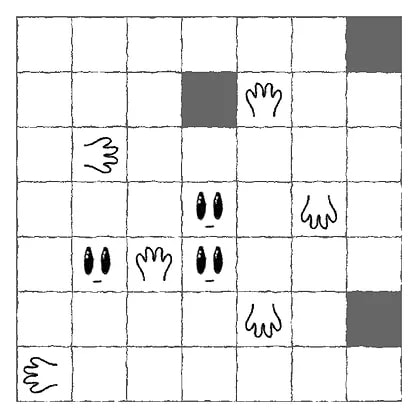
The solutions are shown below.



Please confirm you want to block this member.
You will no longer be able to:
Please allow a few minutes for this process to complete.