Ants Maze
Find a non-intersecting closed path, passing through all four ants, which traverses this double-sided maze. You can not switch between the top and the bottom side of the path at any times.
SOLUTION
The solution is shown below.
Difficulty: Advanced
DescriptionDave Phillips is a maze and puzzle designer, and writer of The Zen Of The Labyrinth—Mazes For The Connoisseur. Phillips has provided puzzles for Reader's Digest, Highlights, National Geographic World, Die Zeit, Ranger Rick, Omni, Games, Scientific American, and United Features Syndicate.
FEATURED
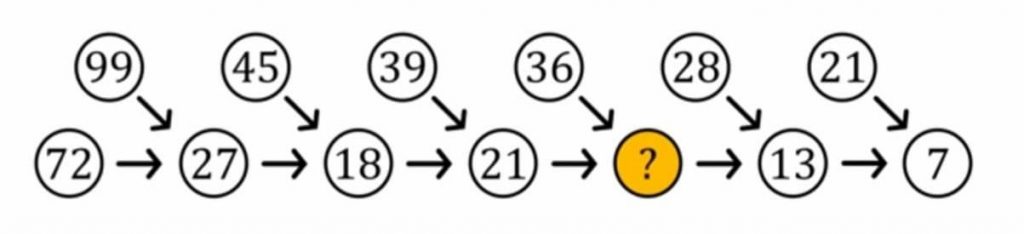
Gun Duel
Mick, Nick, and Rick arrange a three-person gun duel. Mick hits his target 1 out of every 3 times, Nick hits his target 2 out of every 3 times, and Rick hits his target every time. If the three are taking turns shooting at each other, with Mick starting first and Nick second, what should be Mick’s strategy?
SOLUTION
Clearly, Mick should not aim for Nick, because if he kills him, then he will be killed by Rick. Similarly, Nick should not aim for Mick, because if he kills him, then he also will be killed by Rick. Therefore, if Rick ends up against alive Mick and Nick, he will aim at Nick, because he would prefer to face off a weaker
Thus, if Mick shoots at Rick and kills him, then he will have to face off Nick with chance of survival less than 1/3. Instead, if he decides to shoot in the air, then he will face off Nick or Rick with chance of survival at least 1/3. Therefore, Mick’s strategy is to keep shooting in the air, until he ends up alone against one of his opponents.
The Number in the Yellow Circle
Which is the missing number in the yellow circle?
SOLUTION
The missing number is 12. Each number is equal to the sum of the digits of the numbers pointing towards it.
Vinculus Puzzles
Circles are particles and lines joining them are bonds. The objective is to find all the hidden values, following these four rules:
- Particle values must be the sum of their bond values.
- Particles can have the following values: 0, 1, 2, 4, 8, 12, 16.
- Bonds can have the following values: 0, 1, 2, 4.
- If two particles have the same value, the bond between them must have value 0.
EASY 
MEDIUM 
HARD
SOLUTION
The solutions are shown below.
Scoring penalties
At some point in Leonel Messi’s career, the football player had less than 80% success when performing penalty kicks. Later in his career, he had more than 80% success when performing penalty kicks. Show that there was a moment in Leonel Messi’s career
SOLUTION
Let us see that it is impossible for Messi to jump from under 80% success rate to over 80% success rate in just one attempt. Indeed, if Messi’s success rate was below 80% after N attempts, then he scored at most 4N/5 – 1/5 = (4N-1)/5 times. If his success rate was above 80% after N+1 attempts, then he scored at least 4(N+1)/5 + 1/5 = (4N-1)/5 + 6/5 times. However, Messi can not score more than one goal in a single attempt, which completes the proof.
Five Men in the Rain
There were five men going to church and it started to rain. The four that ran got wet and the one that stood still stayed dry.
SOLUTION
Four of the men were carrying a dead man in a coffin to his funeral.
Sequence 4, 2, 3, 4
What is the next number in this sequence:
4, 2, 3, 4, 6, 2, 4, ?
SOLUTION
The answer is 8. The numbers represent the lengths of the words in the question:
what → 4
is → 2
the → 3
next → 4
number → 6
in → 2
this → 4
sequence → 8
Canals on Mars Maze
Starting with the letter “T” at the bottom, visit all spots exactly once before returning to the beginning, so that the letters you pass through spell a complete sentence.
SOLUTION
The path goes through the letters “T”, “H”, “E”, “R”, “E”, “I”, “S”, “N”, “O”, “P”, “O”, “S”, “S”, “I”, “B”, “L”, “E”, “W”, “A”, “Y”, to spell the sentence “There is no possible way”.
53 Bicycles and a Dead Man
There is a room with a table, 53 bicycles, and four men. One of the four men is dead. How did he die?
SOLUTION
The “bicycles” are the (famous) Bicycle playing cards. The four men were playing poker, but one of them was cheating with an extra card, so he got killed.
Raise Me None
Raise me none and I am unbeaten.
Raise me once and I am excessive.
Raise me twice and I am forward.
Raise me thrice and I am eaten.
All said right, but wrongly spelled.
Who am I?
SOLUTION
The answer is the NUMBER 2:
2⁰ = 1 (“one”), which is unbeaten;
2¹ = 2 (“too”), which is excessive;
2² = 4 (“fore”), which is forward;
2³ = 8 (“ate”), which is eaten.