The Letter E
Click the image to enlarge it and download it. Then print it, cut out the three pieces, and rearrange them so that you get the letter “E”.
SOLUTION
Rearrange the pieces, so that they form the shadow of the letter “E”, as shown below.
Difficulty: Expert
We do not know where this puzzle originated from. If you have any information, please let us know via email.
The Connect Game
Two friends are playing the following game:
They start with 10 nodes on a sheet of paper and, taking turns, connect any two of them which are not already connected with an edge. The first player to make the resulting graph connected loses.
Who will win the game?
Remark: A graph is “connected” if there is a path between any two of its nodes.
SOLUTION
The first player has a winning strategy.
His strategy is with each turn to keep the graph connected, until a single connected component of 6 or 7 nodes is reached. Then, his goal is to make sure the graph ends up with either connected components of 8 and 2 nodes (8-2 split), or connected components of 6 and 4 nodes (6-4 split). In both cases, the two players will have to keep connecting nodes within these components, until one of them is forced to make the graph connected. Since the number of edges in the components is either C^8_2+C^2_2=29, or C^6_2+C^4_2=21, which are both odd numbers, Player 1 will be the winner.
Once a single connected component of 6 or 7 nodes is reached, there are multiple possibilities:
- The connected component has 7 nodes and Player 2 connects it to one of the three remaining nodes. Then, Player 1 should connect the remaining two nodes with each other and get an 8-2 split.
- The connected component has 7 nodes and Player 2 connects two of the three remaining nodes with each other. Then, Player 1 should connect the large connected component to the last remaining node and get an 8-2 split.
- The connected component has 7 nodes and Player 2 makes a connection within it. Then, Player 1 also must connect two nodes within the component. Since the number of edges in a complete graph with seven nodes is C^7_2=21, eventually Player 2 will be forced to make a move of type 1 or 2.
- The connected component has 6 nodes and Player 2 connects it to one of the four remaining nodes. Then, Player 1 should make a connection within the connected seven nodes and reduce the game to cases 1 to 3 above.
- The connected component has 6 nodes and Player 2 connects two of the four remaining nodes. Then, Player 1 should connect the two remaining nodes with each other. The game is reduced to a 6-2-2 split which eventually will turn into either an 8-2 split, or a 6-4 split. In both cases Player 1 will win, as explained above.
FEATURED
Imprisoned Logicians
Two friends, logicians – Ein and Stein – get imprisoned in two distant cells in a castle. Both cells have just one door, and a window with 8 bars in the first cell, and 12 bars in the second cell. The first day both logicians get the same letter from the prison master:
“The total number of bars in the two prison cells in this castle is either 18 or 20. Starting tomorrow, every morning I will go first to Ein and then to Stein, and will ask how many bars the other logician has. If one of you answers correctly, I will immediately let both of you leave the castle. If one of you answers incorrectly, I will execute both of you. Of course, you can always decide not to answer and just stay imprisoned.
I have sent a copy of this letter to you and your friend. There is no point in trying to communicate with him – your cells are far away from each other, and he won’t hear you.”
Will the logicians manage to escape the castle eventually? When will they do it?
SOLUTION
Solution coming soon.
FEATURED
Lost In the Forest
You are lost in the middle of a forest, and you know there is a straight road exactly 1 km away from you, but not in which direction. Can you find a path of distance less than 640 m which will guarantee you to find the road?
SOLUTION
Imagine there is a circle with a radius of 100 m around you, and you are at its center O. Let the tangent to the circle directly ahead of you be t. Then, follow the path:
- Turn left 30 degrees and keep walking until you reach the tangent t at point A for a total of 100×2√3/3 meters, which is less than 115.5 meters.
- Turn left 120 degrees and keep walking along the tangent to the circle until you reach the circle at point B for a total of 100×√3/3 which is less than 58 meters.
- Keep walking around the circle along an arc of 210 degrees until you reach point C for a total of 100×7π/6 which is less than 366.5 meters.
- Keep walking straight for 100 meters until you reach point D on the tangent t.
FEATURED
Kings and Queens
What should follow the sequence of diagrams shown below?
SOLUTION
The diagrams represent consecutive monarchs of England:
- King Edward the 8-th → Ke8
- King George 6-th → Kg6
- Queen Elizabeth 2-nd → Qe2
Therefore, the next diagram should represent King Charles the 3-rd → Kc3.
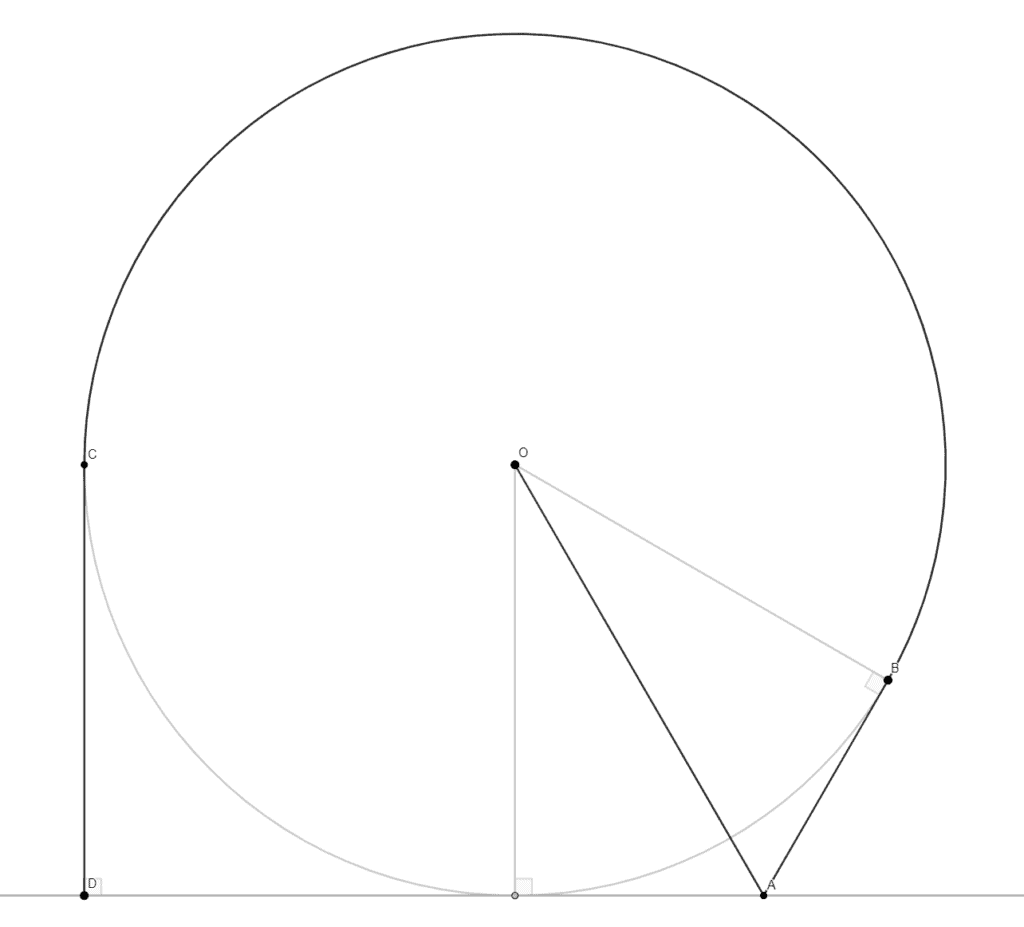
Saavedra Position
White to play. Is this game a win for White, Black, or a draw?
SOLUTION
This game is a win for White.
1. c7 Rd6+
2. Kb5 Rd5+
3. Kb4 Rd4+
4. Kb3 Rd3+
5. Kc2! Rd4!
6. c8=R! Ra4
7. Kb3
Now Black will either lose the rook, or get mated in one. If White promoted a Queen instead of a Rook, then 6… Rc4+ would lead to 7. Qxc4, which is a stalemate.
FEATURED
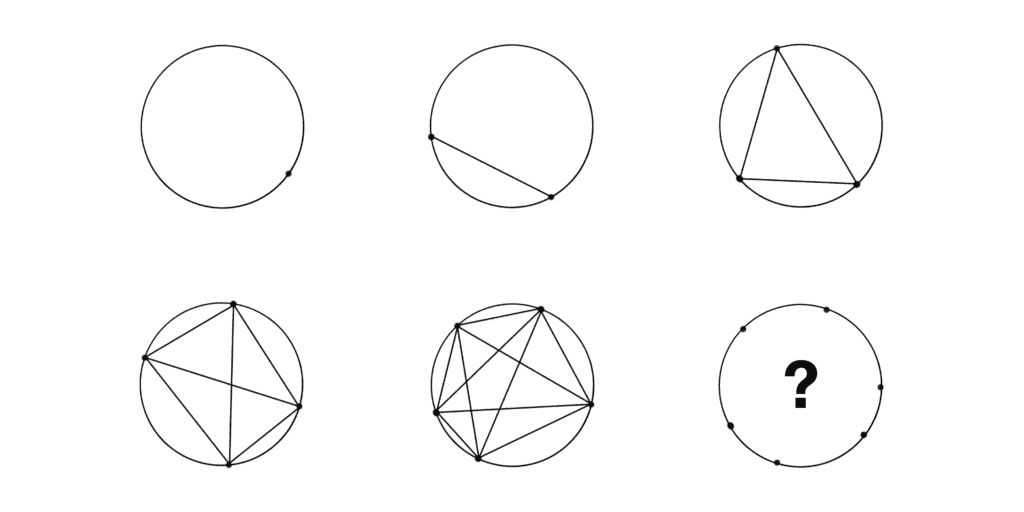
A Broken Circle
There are N points on a circle. If we draw all the chords connecting these points and no three of them intersect at the same point, in how many parts will the interior of the circle get broken?
For example, when N is equal to 1, 2, 3, 4, and 5, we get 1, 2, 4, 8, and 16 parts respectively.
SOLUTION
The answer, somewhat surprisingly, is not 2ᴺ⁻¹, but 1 + N(N-1)/2 + N(N-1)(N-2)(N-3)/24.
In order to see that, we start with a single sector, the interior of the circle, and keep successively drawing chords. Every time we draw a new chord, we increase the number of parts by 1 and then add 1 extra part for each intersection with previously drawn chords.
Therefore, the total number of parts at the end will be:
1 + the number of the chords + the number of the intersections of the chords
Each chord is determined by its 2 endpoints and therefore the number of chords is N(N-1)/2.
Each intersection is determined by the 4 endpoints of the two intersecting chords and therefore the number of intersections is N(N-1)(N-2)(N-3)/4!.
A Short, Brutal Riddle
Left alone, I’m a word with five letters.
I’m honest and fair, I’ll admit.
Rearranged, I’m of no use to trains.
Again, and I’m an overt place, warm and well lit.
What am I?
SOLUTION
The answer is LIAR. After rearranging the letters, you can get RAIL – important for trains, or LAIR – a dark, hidden place. Since the riddler is a liar, the resulting words are exactly the opposite of his descriptions.
Source:
FEATURED
Sum Up to 15
Tango and Cash are playing the following game: Each of them chooses a number between 1 and 9 without replacement. The first one to get 3 numbers that sum up to 15 wins. Does any of them have a winning strategy?
SOLUTION
Place the numbers from 1 to 9 in a 3×3 grid so that they form a magic square. Now the game comes down to a standard TIC-TAC-TOE, and it is well-known that it always leads to a draw when both players use optimal strategies.
FEATURED
David Copperfield
David Copperfield and his assistant perform the following magic trick. The assistant offers a person from the audience to pick 5 arbitrary cards from a regular deck and then hands them back to him. After the assistant sees the cards, he returns one of them to the audience member and gives the rest one by one to David Copperfield. After the magician receives the fourth card, he correctly guesses what card the audience member holds in his hand. How did they perform the trick?
SOLUTION
Out of the five cards, there will be (at least) two of the same suit; assume they are clubs. Now imagine all clubs are arranged in a circle in a cyclic manner – A, 2, 3, … J, Q, K (clock-wise), and locate the two chosen ones on it. There are two arks on the circle which are connecting them and exactly one of them will contain X cards, with X between 0 and 5. Now the assistant will pass to David Copperfield first the clubs card which is located on the left end of this ark, will return to the audience member the clubs card which is located on the right end of it and, with the remaining three cards, will encode the number X. In order to do this, he will arrange the three extra cards in increasing order – first clubs A-K, then diamonds A-K, then hearts A-K and finally spades A-K. Let us call the smallest card in this order “1”, the middle one “2” and the largest one “3”. Now, depending on the value of X, the assistant will pass the cards “1”, “2” and “3” in the following order:
X=0 ⇾ 1, 2, 3
X=1 ⇾ 1, 3, 2
X=2 ⇾ 2, 1, 3
X=3 ⇾ 2, 3, 1
X=4 ⇾ 3, 1, 2
X=5 ⇾ 3, 2, 1
In this way David Copperfield will know the suit of the audience member’s card and also with what number he should increase the card he received first in order to get value as well. Therefore, he will be able to guess correctly.