Hard – Page 2 – Puzzle Prime

Cut the Pizza

Section: Brain Teasers Category: Mathematics

Difficulty: Hard Tags: Geometry

Cut a circular pizza into 12 congruent slices, such that exactly half of them contain crust.

Remark: We say that a slice contains crust if it shares an arc with the boundary of the pizza (with non-zero measure).

SOLUTION

First, cut the pizza into 6 congruent circular triangles, and then split each of them in half, as shown on the image below.

Unknown Author July 13, 2023

4 Comments

Spot the Robber

Section: Brain Teasers Category: Mathematics

Difficulty: Hard

The streets of the city are a square grid that extends infinitely in all directions. One of the streets has a police officer stationed every 100 blocks and there is a robber is somewhere in the city.

Can you devise a strategy that guarantees the robber will be spotted by a police officer at some point, no matter how he tries to avoid them?

Note: The officers can see infinitely far, but their running speeds are lower than the speed of the robber.

SOLUTION

Let the police officers are located at points with coordinates (100N, 0) for N = 0, ±1, ±2… First, we fix the positions of all officers stationed at points (±200N, 0), then repeatedly perform the following procedure, step by step:

On step M, we let the non-fixed officers who are closest to the center move to the free points with coordinates (K, 0) and (0, K) for K = 0, ±1, ±2, … ±M. Then we fix their positions.

Since there are fixed officers at points (200N, 0) at all times, the robber is contained within some vertical strip the entire time. Therefore, at some point there will be two fixed officers that will restrict the robber within a horizontal segment of size 1, at coordinates (x, T) for x ∈ (S, S+1) and some T. Finally, at some point an officer will move to the point (0, T) and will spot the robber.

Alex Lvovsky June 13, 2023

0 Comments

Symm-Sala-Bim

Section: Brain Teasers Category: Deduction

Difficulty: Hard

Rearrange the three polyominoes so that they form a symmetrical shape.

SOLUTION

The solution is shown below.

Alexander Magyarics May 4, 2023

0 Comments

A Bunch of Words

Section: Casual Puzzles Category: Rebus

Difficulty: Hard Tags: Words

Examine the 12 words below and determine what popular proverb is represented by them.

mimic	iris	picnic
pilgrim	love	giving
love	rigid	icing
spirit	vigil	crisis

SOLUTION

The answer is LOVE IS BLIND.

All the words in the table have 2 “eyes” (i’s), except for the word “love”.

Unknown Author April 1, 2023

0 Comments

Clean Death

Section: Brain Teasers Category: Science

Difficulty: Hard

A man was going to bleach his socks because they had gotten muddy the day before. As he was pouring the bleach into the washing machine, he spilled some on the floor. He got some cleaning fluid and mopped it up with a rag. Minutes later he was dead. What killed him?

SOLUTION

When the ammonia (NH₃), found in cleaning fluids, is mixed with bleach (a dilute solution of sodium hypochlorite, NaOCl), a deadly gas (monochloramine, NH₂Cl) is produced that can kill a person instantly. The resulting chemical reactions are the following:

Bleach decomposes, forming hydrochloric acid and subsequently chlorine gas:
NaOCl → NaOH + HOCl
HOCl → HCl + O
NaOCl + 2HCl → Cl₂ + NaCl + H₂O
The chlorine gas reacts with the sodium hypochlorite in the bleach, releasing chloramine as a vapor:
2NH₃ + Cl₂ → 2NH₂Cl

Unknown Author March 25, 2023

3 Comments

STANDARD Word

Section: Brain Teasers Category: Insight

Difficulty: Hard

Given the word STANDARD, take away two letters and then add three digits to make a logical sequence.

SOLUTION

Remove the two letters A to get ST-ND-RD and then add the digits 1, 2, 3 to get 1ST-2ND-3RD.

Unknown Author March 7, 2023

0 Comments

FEATURED

The Bicycle Problem

Section: Brain Teasers Category: Science

Difficulty: Hard Tags: Featured

If you pull straight back on a pedal of a bicycle when it is at its lowest position, will the bicycle move forward or backward?

SOLUTION

The surprising answer is that (usually) the bicycle will move backward.

When a bicycle moves forward, the trajectory its pedal traces with respect to the ground is called a trochoid. Depending on the selected gear of the bicycle, that trochoid could be:

Curtate trochoid (for almost all gears of most bicycles)
Prolate trochoid (if the gear is very low and the bicycle moves slowly)
Common trochoid, a.k.a. cycloid (if the wheels of the bicycle and the pedal spin at identical speeds, practically never happens)

Since we are fixed with respect to the ground, by pulling the pedal backward, we are causing it to move leftward along the trochoid and therefore the bicycle will be moving backward. We note that despite that, the pedal will be moving forward with respect to the bicycle (but not with respect to the ground).

You can see a visual explanation of this puzzle in the video below.

Unknown Author January 1, 2023

2 Comments

Leave No Squares

Section: Brain Teasers Category: Deduction

Difficulty: Hard Tags: Matchsticks

How many matchsticks do you need to remove so that no squares of any size remain?

SOLUTION

Nine matchsticks are enough, as seen from the solution below.

To see that eight matchsticks are not enough, notice that removing an inner matchstick reduces the number of 1×1 squares at most by 2. Since there are 16 such small squares, in order to get rid of them all, we need to remove only inner matchsticks. However, in this case, the large 4×4 square will remain.

Unknown Author December 19, 2022

0 Comments

Symmetry and Perplexion

Section: Brain Teasers Category: Mathematics

Difficulty: Hard

Find an X > 1, such that:

SOLUTION

If we pick X=√2, (using a somewhat ambiguous notation) we get:

To see that the equality above holds, simply note that 2=(√2)² and take √2 root of both sides.

Unknown Author November 28, 2022

0 Comments

Conflicting Words

Section: Brain Teasers Category: Insight

Difficulty: Hard Tags: Words

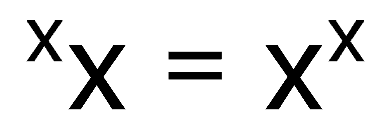
What unique feature do the following words share?

FRIEND, FEAST, THERE, THOROUGH, FLIGHT, WONDERFUL, RESIGN, ENDURING, PEST, COVERT

SOLUTION

Each of these words contains its antonym as a sub-word:

FRIEND – FIEND, FEAST – FAST, THERE – HERE, THOROUGH – ROUGH, FLIGHT – FIGHT, WONDERFUL – WOEFUL, RESIGN – REIGN, ENDURING – ENDING, PEST – PET, COVERT – OVERT

Unknown Author October 4, 2022

0 Comments