Hard – Page 5 – Puzzle Prime

FEATURED

Cut and Arrange

Section: Brain Teasers Category: Practical

Difficulty: Hard Tags: Featured

Get a piece of paper with dimensions 9×12 with a 1×8 rectangular hole in the middle. Then, cut the paper into two pieces that can be arranged into a square. You can print out the shape below.

SOLUTION

The solution is shown below.

Unknown Author May 13, 2021

0 Comments

Normal Person

Section: Casual Puzzles Category: Riddle

Difficulty: Hard

I caused my mother’s death and didn’t get convicted.
I married 100 women and never got divorced.
I got born before my father, but I am considered perfectly normal?

Who am I?

SOLUTION

A priest, whose mother dies from labor, who marries 100 women to 100 men, and whose father attends his birth.

Unknown Author March 28, 2021

0 Comments

Crashing Light Bulbs

Section: Brain Teasers Category: Insight

Difficulty: Hard

You are living in a 100-floor apartment block. You know that there is one floor in the block, such that if you drop a light bulb from there or anywhere higher, it will crash upon hitting the ground. If you drop a light bulb from any floor underneath it however, the light bulb will remain intact. If you have two light bulbs at your disposal, how many drop attempts do you need such that you can surely find which the floor in question is?

SOLUTION

The answer is 14 drops. You can do this by throwing the first bulb from floors 14, 27, 39, 50, 60, 69, 77, 84, 90, 95, 99, 100 (notice that the difference decreases always by 1) until it crashes and then start throwing the second bulb from the floors in between. For example, if the first bulb crashes at floor 69, you start throwing the second bulb from floors 61, 62, 63, etc. This way the total number of throws would be always at most 14.

Proving that 14 is optimal is done using the same logic. In order to use at most 13 throws, the first throw should be made from floor 13 or lower. The second throw should be made from floor 13+12 or lower, the third throw should be made from floor 13+12+11 or lower, etc. Continuing with the same argument, we conclude that the 13th drop should be made from floor 13+12+…+2+1=91 or lower. However, if the first light bulb does not crash after the last throw, you will not be able to find out which number among 92-100 is X.

Unknown Author March 7, 2021

8 Comments

Coins on a Chessboard

Section: Brain Teasers Category: Mathematics

Difficulty: Hard

There is a room with a chessboard inside. On each of its 64 squares, there is placed a coin, either heads up or heads down. You enter the room and a person inside points towards one special square on the chessboard and gives you the chance to flip one of the coins (whichever you choose). Then you leave the room, your friend enters and has to guess which was the special square on the chessboard. If you two could devise a plan before entering the room, how would you make sure your friend always guesses correctly which is the special square?

SOLUTION

First, you must enumerate the coins with numbers from 1 to 64, locate the mystery coin, and calculate the binary representation of its number, padded with zeros on the left to 6 digits length. For example, if the mystery coin is the 5th one on the 4th row, its number would be 29 and will have a binary representation 011101. Then, consider the following sets of coins:

A1 = {row 1, row 2, row 3, row 4}
A2 = {row 1, row 2, row 5, row 6}
A3 = {row 1, row 3, row 5, row 7}
A4 = {column 1, column 2, column 3, column 4}
A5 = {column 1, column 2, column 5, column 6}
A6 = {column 1, column 3, column 5, column 7}

Now, the strategy is to flip the coin which makes the parity of heads in set Ai odd if and only if the i-th digit in the binary representation of the mystery coin is 1. It is easy to check that this is always a possible thing to do.

Unknown Author February 27, 2021

4 Comments

The Majority Name

Section: Brain Teasers Category: Mathematics

Difficulty: Hard Tags: Algorithm

In a long list of names, one of the names appears more than half of the time. You will be read the names one at a time, without knowing how many they are, and without being able to write them down. If you have a very weak memory, how can you figure out which is the majority name?

SOLUTION

Remember the first name and then keep track of whether it has been repeated more than half of the time. To do that, simply add 1 if you hear the name or subtract one when you hear another name. If the list finishes and your counter is positive, then the first name is the majority. If your counter drops to 0, simply restart the procedure with the next name you hear.

This algorithm, invented by R. Boyer and J. Moore, works, because if the counter ends up at 0, then each of the names up to that moment has been read at most half of the time. Therefore, the majority name appears more than half of the time in the remainder of the list.

Unknown Author February 6, 2021

1 Comment

Word 123456789

Section: Casual Puzzles Category: Riddle

Difficulty: Hard

I have a 9 letter word, 123456789.
If I lose it, I die.
If I have 234, I can 1234.
If I have 56, I am very sick.
235 is the same as 789.
What is the word?

SOLUTION

The answer is HEARTBEAT.

Unknown Author January 31, 2021

3 Comments

Ambiguous Clock

Section: Brain Teasers Category: Mathematics

Difficulty: Hard

The hands of my alarm clock are indistinguishable. How many times throughout the day their positioning is such that one cannot figure out which is the hour hand, and which is the minute hand?

Remark: AM-PM is not important.

SOLUTION

Imagine that you have a third hand which moves 12 times as fast as the minute hand. Then, at any time, if the hour hand moves to the location of the minute hand, the minute hand will move to the location of the imaginary hand. Therefore, our task is to find the number of times during the day when the hour hand and the imaginary hand are on top of each other, and the minute hand is not.

Since the imaginary hand moves 144 times faster than the hour hand, the two hands are on top of each other exactly 143 times between 12AM and 12PM. Out of these 143 times, 11 times all three arrows are on top of each other. Therefore, we have 2 × (143 – 11) = 264 times when we cannot figure out the exact time during the entire 24-hour cycle.

Unknown Author January 27, 2021

1 Comment

Einstein’s Puzzle

Section: Brain Teasers Category: Deduction

Difficulty: Hard

There are 5 houses and each of them has a different color. Their respective owners have different heritages, drink different types of beverages, smoke different brands of cigarettes, and look after different types of pets. It is known that:

The Brit lives in the red house.
The Swede keeps dogs as pets.
The Dane drinks tea.
Looking from in front, the green house is just to the left of the white house.
The green house’s owner drinks coffee.
The person who smokes Pall Malls raises birds.
The owner of the yellow house smokes Dunhill.
The man living in the center house drinks milk.
The Norwegian lives in the leftmost house.
The man who smokes Blends lives next to the one who keeps cats.
The man who keeps a horse lives next to the man who smokes Dunhill.
The owner who smokes Bluemasters also drinks beer.
The German smokes Prince.
The Norwegian lives next to the blue house.
The man who smokes Blends has a neighbor who drinks water.

The question is, who owns the pet fish?

SOLUTION

The German owns the pet fish.

Since the Norwegian lives in the leftmost house (9) and the house next to him is blue (14), the second house must be blue. Since the green house is on the left of the white house (4), the person living in the center house drinks milk (8), and the green house’s owner drinks coffee (5), the fourth house must be green and the fifth one must be white. Since the Brit lives in the red house (1) and the Norwegian lives in the leftmost house (9), the leftmost house must be yellow and the center house must be red. Therefore, the colors of the houses are: YELLOW, BLUE, RED, GREEN, WHITE.

Since the Norwegian from the yellow house smokes Dunhill (7), the man from the blue house must keep a horse (11). The person smoking Blends cannot be in the red house, because this would imply that the person in the green house keeps cats and the Swede keeps dogs in the white house (2, 10). However, in this case the Dane must be drinking tea in the blue house (3) and the person smoking Blends does not have a neighbor drinking water (5), which is a contradiction (15). Also, the person smoking Blends cannot be in the green house, because this would imply that the person in the white house drinks water (15), the Dane lives in the blue house (3), and the German and the Swede live in the last two houses. Since the German smokes Prince (13) and the Swede keeps dogs (2), there is nobody who could smoke Bluemaster and drink beer (12). The person smoking Blends cannot be in the white house either, because this would imply that the person in the green house drinks water (15), when in fact he drinks coffee (5).

Therefore, the person smoking Blends must be in the blue house, and then the German and the Swede must live in the last two houses (2, 13). Since the person who smokes Bluemasters drinks beer (12), this must be the Swede with his dogs in the white house (2). The only option for the person who smokes Pall Mall and raising birds (6) is the red house. Then the Norwegian must keep cats (10) and the German is left with the pet fish in the green house.

Albert Einstein October 24, 2020

0 Comments

Close the Loop

Section: Brain Teasers Category: Mathematics

Difficulty: Hard

Alex and Bob are playing a game. They are taking turns drawing arrows over the segments of an infinite grid. Alex wins if he manages to create a closed loop, Bob wins if Alex does not win within the first 1000 moves. Who has a winning strategy if:

a) Alex starts first (easy)
b) Bob starts first (hard)

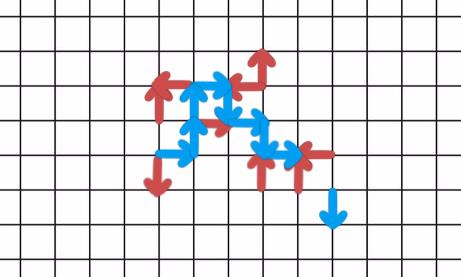
Remark: The loop can include arrows drawn both by Alex and Bob.

SOLUTION

In both cases, Bob wins. An easy strategy for part a) is the following:

Every time Alex draws an arrow, Bob draws an arrow in such a way that the two arrows form an L-shaped piece and either point towards or away from each other. Since every closed loop must contain a bottom left corner, Alex cannot win.

For part b), Bob should use a modification of his strategy in part a). First, he draws a horizontal arrow. Then, he splits the remaining edges into pairs, as shown in the image below. If Alex draws one arrow on the grid, then Bob draws its paired arrow, such that the two arrows point either towards or away from each other. The only places where a loop can have a bottom left corner are where Bob drew the first arrow or the grid points directly above it. However, if a loop has a bottom left corner there, then it is easy to see that it must have at least one more bottom left corner elsewhere, which is impossible.

Unknown Author October 12, 2020

0 Comments

Mate in the Fourth

Section: Brain Teasers Category: Chess

Difficulty: Hard

The first four moves played by White are 1. f3, 2. Kf2, 3. Kg3, 4. Kh4. If White gets mated in the fourth move, what could be the moves played by Black?

SOLUTION

The game proceeds as follows:

1. f3 e5 (or e6)
2. Kf2 Qf6
3. Kg3 Qxf3+
4. Kh4 Be7#

Boris Zlotnik August 21, 2020

11 Comments