We do not know where this puzzle originated from. If you have any information, please let us know via email.
There is a property that applies to all words in the first list and to none in the words in the second list. What is it?
The words in the first list are called “Abecederian”, i.e. their letters are in alphabetical order.
A long time ago there was a kingdom, isolated from the world. There was only one way to and from the kingdom, namely through a long bridge. The king ordered the execution of anyone caught fleeing the kingdom on the bridge and the banishment of anyone caught sneaking into the kingdom.
The bridge was guarded by one person, who was taking a 10-minute break inside his cabin every round hour. Fifteen minutes were needed for a person to cross the bridge and yet, one woman managed to escape the kingdom. How did she do it?
Once the guard entered the cabin, the woman started crossing the bridge for 9 minutes, and then turned around and pretended to be going in the opposite direction for one more minute. When the guard caught her, she said she was trying to enter the kingdom, so he banished her away.
A man is found unconscious in front of a store at two in the morning. His head is bleeding and there is a brick laying next to him. When the police arrive, they carry the man to jail. Why did they arrest him?
The man was a burglar who tried to break the store’s glass with the brick. The glass turned out to be bullet proof, so the brick bounced back and hit him in the head, knocking him out.
Can you figure out what common phrases these rebuses represent?
The answers are:
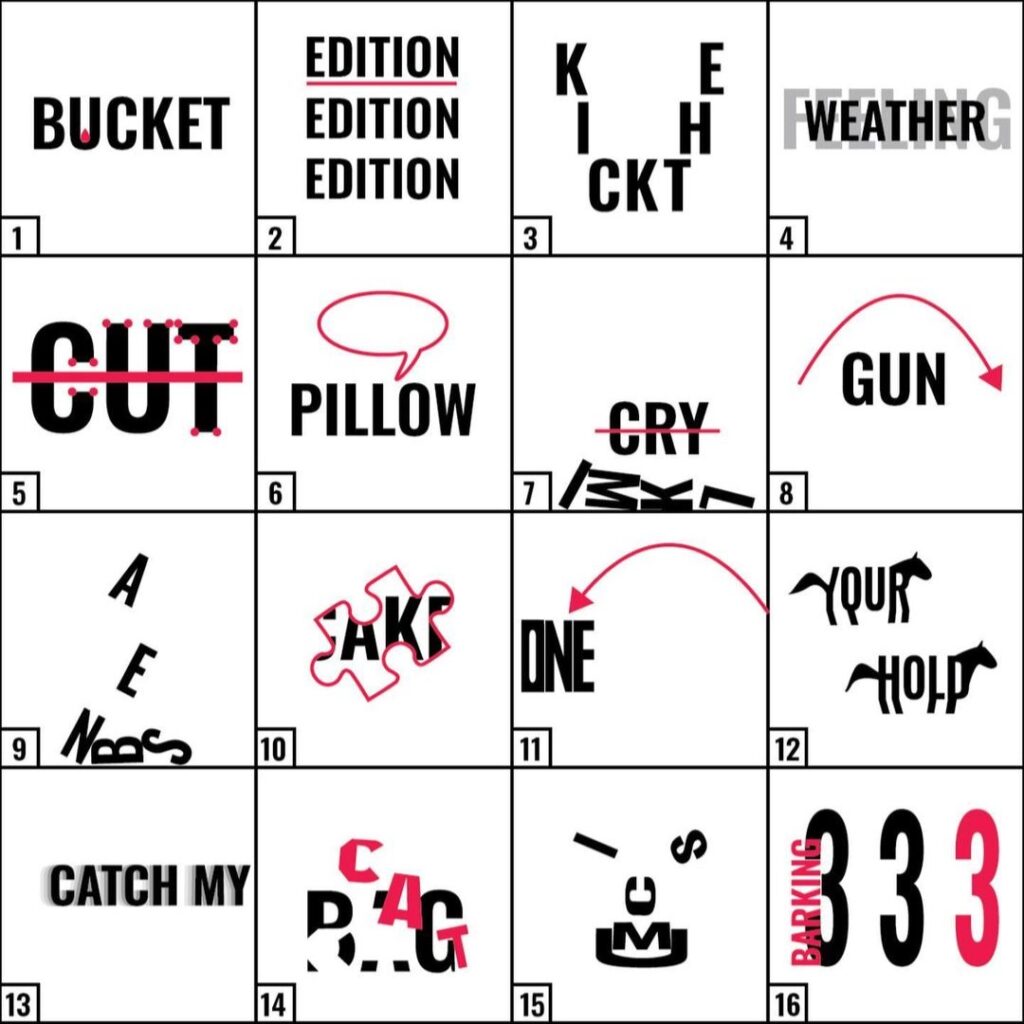
Can you recognize the four words below?
If you rotate the screen by 90°, you will read vertically:
A string is wound around a circular rod with circumference 10 cm and length 30 cm. If the string goes around the rod exactly 4 times, what is its length?
Imagine the circular rod is actually a paper roll and the string is embedded inside the paper. When we unroll it, we get a paper rectangle 30cm×40cm with the string embedded along the diagonal. Using the Pythagorean theorem, we find that the length of the string is 50cm.
I have a heart that doesn’t beat.
I have a mouth that doesn’t speak.
I have a head that doesn’t think.
What am I?
The answer is ARTICHOKE.
An ant is positioned at one of the vertices of a cube and wants to get to the opposite vertex. If the edges of the die have length 1, what is the shortest distance the ant needs to travel?
We unfold a cube to get a cross-shaped figure. Then, the problem is to find the shortest path between two points separated by a horizontal distance of 2 units and a vertical distance of 1 unit.
It is easy to see that the path in question is the one passing through the middle of the edge between the start and end points, and which has a distance of √5.
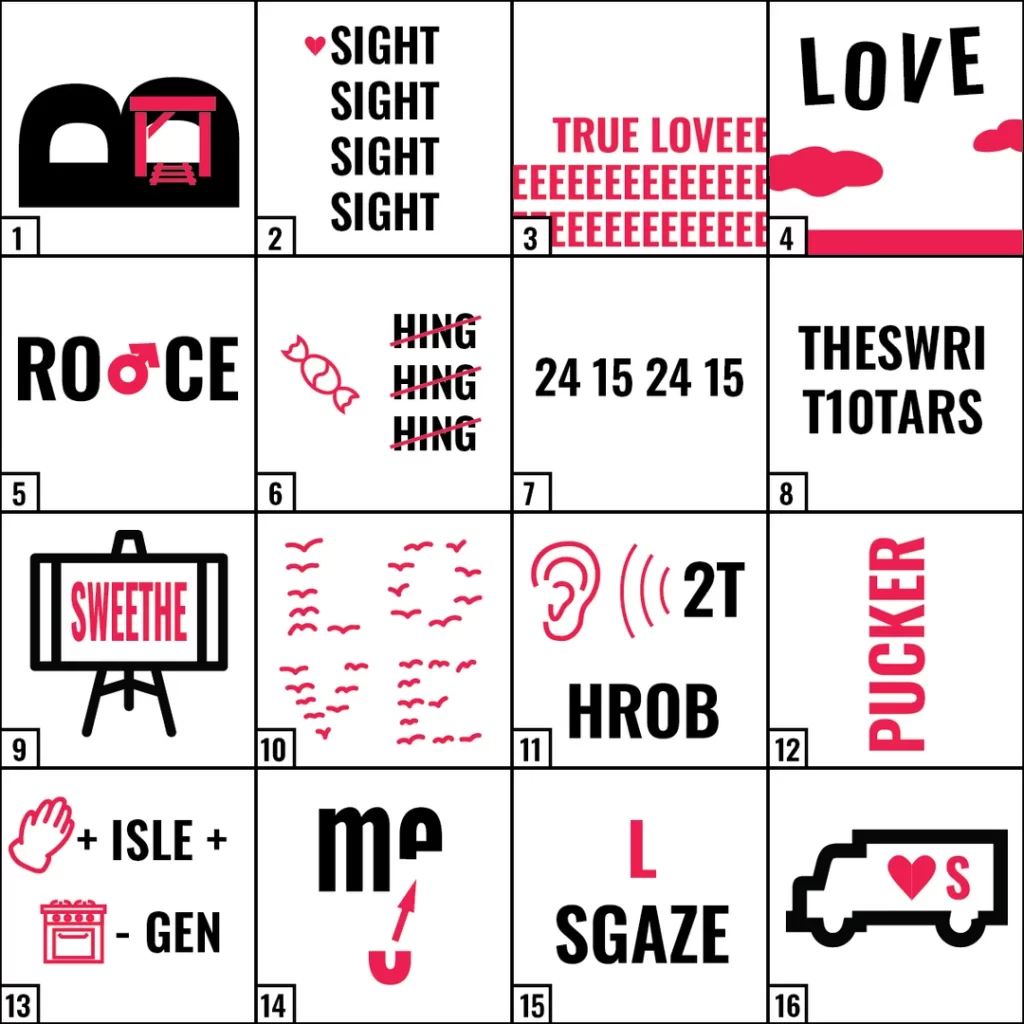
Can you figure out what these love-related expressions these rebuses represent?
The answers are:
There is a square drawn on a piece of paper and also a point marked with invisible ink. You are allowed to draw 3 lines on the paper and for each of them you will be told whether the point is on its left, on its right, or lies on the line. Your task is to find out whether the point is inside the square, outside the square, or on its boundary. How do you do it?
Draw one of the diagonals of the square. Then, draw the 2 lines containing the sides of the square that are on the same side as the invisible point.
Please confirm you want to block this member.
You will no longer be able to:
Please note: This action will also remove this member from your connections and send a report to the site admin. Please allow a few minutes for this process to complete.
