We do not know where this puzzle originated from. If you have any information, please let us know via email.
What numbers should you put on the sides of two cubes, so that every date of the month can be expressed using these cubes?
You put the numbers 0, 1, 2, 3, 4, 5 on the first die and the numbers 0, 1, 2, 7, 8, 6/9 on the second die.
When do the hour and the minute hands of the clock lie on top of each other, and also between the numbers 1 and 2?
One such time is around 1:05 – at 1 o’clock and 5.454… minutes. This can be easily found by solving the linear equation x = 12(x – 5) => x=60/11.
Another time you possibly didn’t think about is 12:00 o’clock. At that time, the hour and minute hands are on top of each other and just between the two digits of the number 12.
Get from START to FINISH in this special maze created by Joe Wos for Puzzle Prime.
The solution is shown below.
John gets off work at random times between 3 and 5 PM. His mother lives uptown, his girlfriend lives downtown. John takes the first subway that comes in either direction and eats dinner with the one he is delivered to. Even though John believes he has 50-50 chance to have dinner with either his mother or his girlfriend, he visited the former only 2 times out of the last 20. How come?
The subway heading downtown arrives at 3:00, 3:10, 3:20, etc, and the subway heading uptown arrives at 3:01, 3:11, 3:21, etc. Thus, the chance that John goes to his girlfriend is about 90% (depending on train delays).
First, get a completely untangled rope. Now, your task is to grab its two ends, and without letting it go, tie this knot in the middle.
In order to do this, first cross your arms, and from this position, grab the two ends of the rope. Once you untangle your arms, the knot will appear on the rope.
Can you see which letters are connected with each other in this 3D maze?
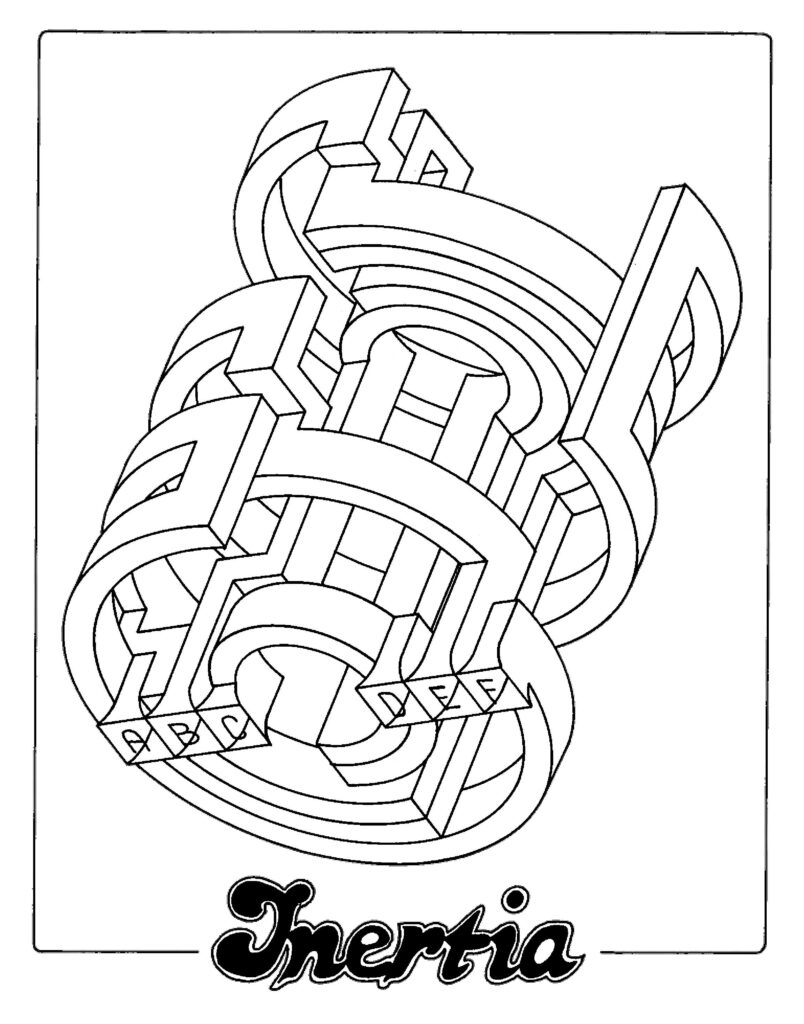
The solution is shown below.
None of these statements is correct.
At most 1 of these statements is correct.
At most 2 of these statements are correct.
…
At most 98 of these statements are correct.
At most 99 of these statements are correct.
How many of these statements are correct?
If the number of true statements is X, then statements 1, 2, … , X are wrong, and the rest are correct. Therefore X = 100 – X and X = 50. Thus, there are 50 correct statements.
Get from START to FINISH in this landscape maze, created by Matthew Haussler.
The solution is shown below.
Consider an arbitrary acute triangle ABC. Let E be the intersection of the bisector at vertex C and the bisection of the side AB. Let F and G be the projections of E on AC and BC respectively.
Since E belongs to the bisection of AB, we must have AE = BE. Also, since E belongs to the bisector of C, we must have EF = EG. However, this would imply that triangles AEF and BGF are identical, and then AF = BF. We also have that CF = CG, which implies that AC = BC. The arbitrarily chosen triangle ABC is isosceles!
Can you find where the logic fails?
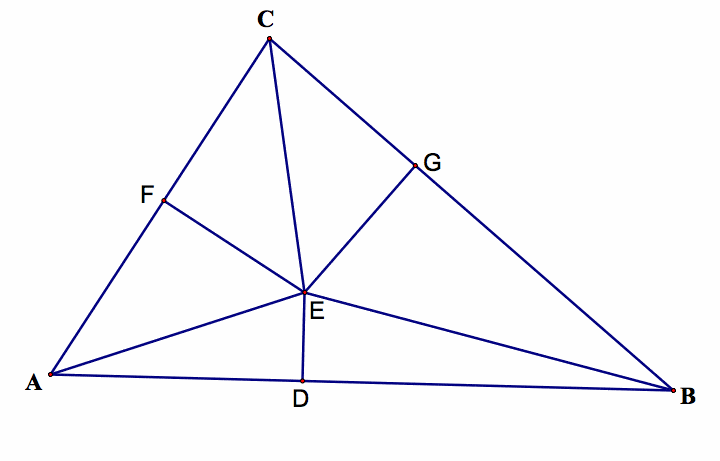
The bisector of C and the bisection of AB always intersect outside the triangle, on the circumcircle. One of the points F and G always lies on the segment AC or BC, and the other one does not.
It is White’s move next. Is this game a win for Black or a draw?
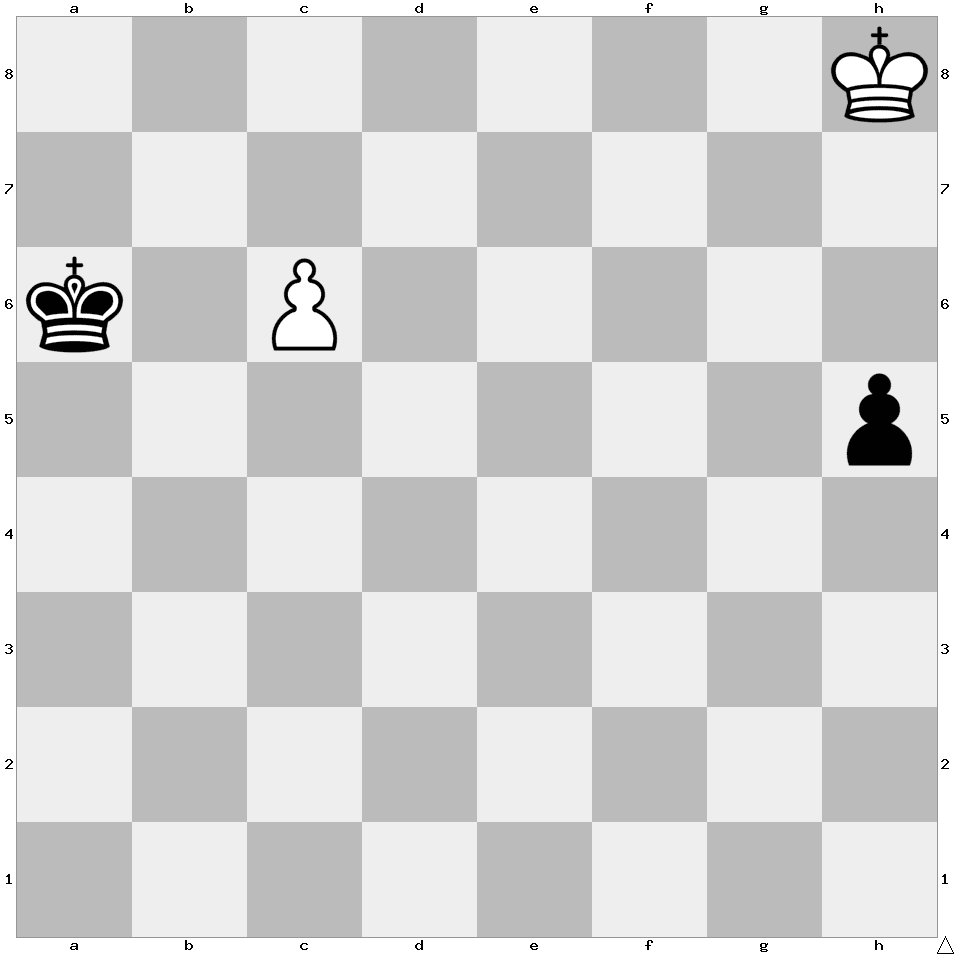
The game is a draw. The first two moves of White are Kg7 and Kf6. If Black moves the king twice in the meantime, then White can get to the pawn on the h-file and take it. If Black moves the king once, then White plays Ke5. If Black moves the king again, White can take the pawn on the h-file. Otherwise, White plays Kd6 and can promote his pawn right after Black promotes his. Finally, if after Kg7 and Kf6 Black moves the pawn twice, then White plays Ke7, and once again can promote his pawn right after Black promotes his.
Please confirm you want to block this member.
You will no longer be able to:
Please allow a few minutes for this process to complete.
