The Least Spoken Language
Which is the least spoken language in the world?
SOLUTION
The answer is THE SIGN LANGUAGE.
Difficulty: Medium
We do not know where this puzzle originated from. If you have any information, please let us know via email.
Peculiar Sequence of Words
What is the peculiar property of this sequence of words?
WHAT, HOLE, ALES, TEST
SOLUTION
If you take the first letter from each word, you will spell the first word in the sequence.
If you take the second letter from each word, you will spell the second word in the sequence.
If you take the third letter from each word, you will spell the third word in the sequence.
If you take the fourth letter from each word, you will spell the fourth word in the sequence.
| W | H | A | T |
| H | O | L | E |
| A | L | E | S |
| T | E | S | T |
Ten Matchsticks
You have these fifteen matchsticks. Remove six of them and leave ten.
SOLUTION
Remove 6 matchsticks and leave 9 that spell the word TEN.
Dead Man in a Hut
One day, the police found a man dead inside a hut. In his left hand, he was holding a gun. In his right hand, he had a recording device. When the recording was played, the police heard the man talking about how horrible his life was and how he wanted it to end. The recording ended with a gunshot. The police was about to call it a suicide until one detective pointed out a very important clue. What was it?
SOLUTION
If the man shot himself with the gun, then he would not have been able to stop recording with the device.
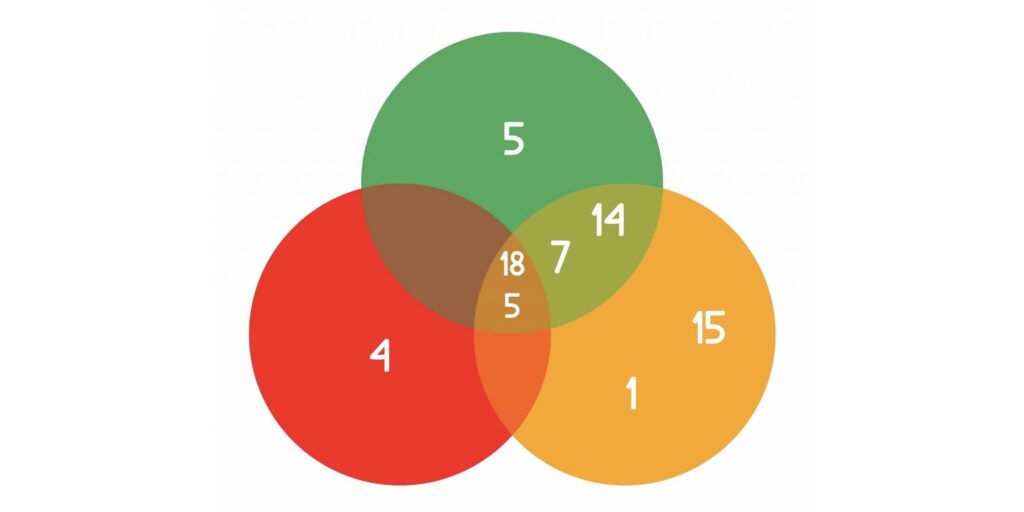
Color Venn
What does this Venn diagram depict?
SOLUTION
Each of the numbers corresponds to a letter from the alphabet:
1 – A, 4 – D, 5 – E, 7 – G, 14 – N, 15 – O, 18 – R
The three colors in the Venn diagram are GREEN, RED, YELLOW, and what is depicted is the letters they share.
Alive Without Breath
Alive without breath,
As cold as death;
Never thirsty, ever drinking,
All in mail never clinking.
SOLUTION
The answer is FISH.
Splitting Coins
You split 1000 coins into two piles and count the number of coins in each pile. If there are X coins in pile one and Y coins in pile two, you multiple the two numbers to get XY. Then you split both piles further, repeating the same counting and multiplication process, and adding the new multiplication results to the first one. The process ends when you end up with 1000 single-coin piles. Prove that you will always get the same final result, no matter how the piles have been divided during the splitting process.
For example, if you start with 5 coins and split them into a pile of 2 and a pile of 3, you get the number 2×3=6. Then, if you split the pile of 3 into a pile of 1 and a pile of 2, you will add 1×2=2 more to the 6 and get 8. Finally, if you split the two piles of 2 into single-coin piles, you will end up with 8+1+1=10.
SOLUTION
Consider the sum of the squares of the numbers of coins in each pile, plus twice the sum of the products. On each step, if you split a pile of X+Y coins into a pile of X coins and a pile of Y coins, the sum of the squares will get reduced by 2XY, exactly the amount the sum of the products will increase by. Therefore, that number remains constant throughout the entire process and ends up exactly (1000²-1000)/2=499500.
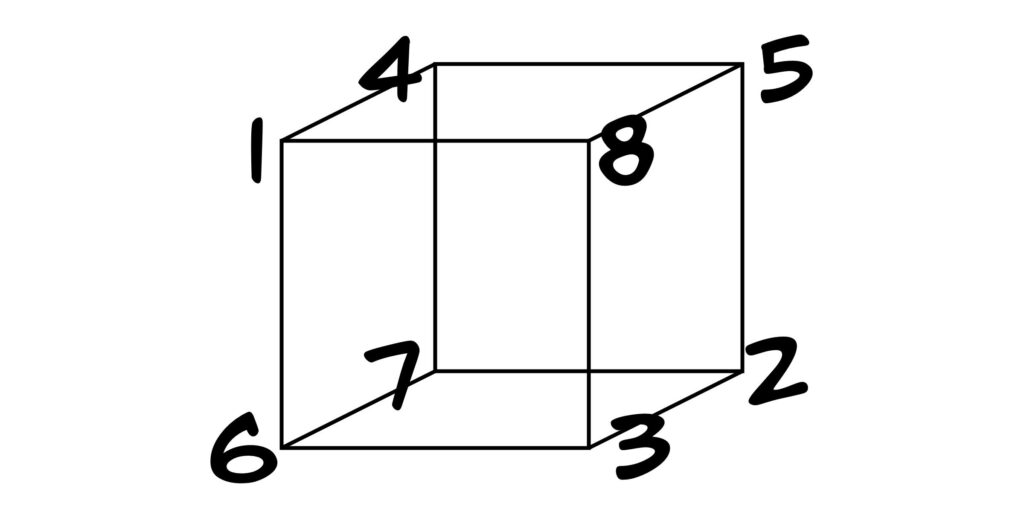
1 to 8 on a Cube
Place the numbers from 1 to 8 on the vertices of a cube so that the sum of the four numbers on every face is the same.
SOLUTION
The solution is shown below:
Sequence 1, 3, 7, 12
Which is the next number in the following sequence:
1, 3, 7, 12, 18, 26, 35, 45, 56, ?
SOLUTION
This is the so called Hofstadter Figure-Figure Sequence.
The sequence of the differences between the consecutive numbers in the original sequence is 2, 4, 5, 6, 8, 9, 10, 11… These are exactly the natural numbers missing from the original sequence. Therefore, the next number should be 56 + 13 = 69.
A Cardinal Points
A cardinal points and says, “thorn, shout, seat, and stew.” Can you explain?
SOLUTION
The sentence is a play on words and anagrams. Thorn, shout, seat, and stew are anagrams of the four cardinal directions of the compass: north, south, east, and west.