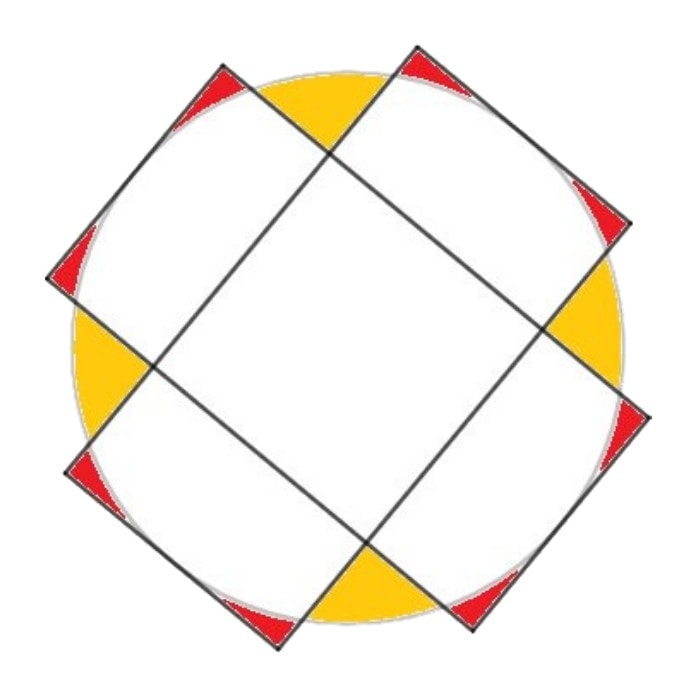
Two Rectangles in a Circle

Which is the larger area: red or orange? The points around the circumference are evenly spaced.

SOLUTION

Let the radius of the circle be $R$ . Then, its area is $S(D) = πR^2$ . The rectangles’ lengths are equal to $2R$ and their widths are equal to $R$ . Therefore,

$S_{rectangle} = 2R^2, \quad S_{square} = R^2$ ,

and then:

$S_{RED} - S_{YELLOW} = 2S_{rectangle} - S_{square} - S_{circle} = 4R^2 - R^2 - πR^2 < 0.$

Thus, the total red area is smaller than the total yellow area.

Puzzle Newsletter

Responses