Two Triangles in a Dodecagon
The difference between the orange and yellow areas is 2. What’s the total area of the regular dodecagon?
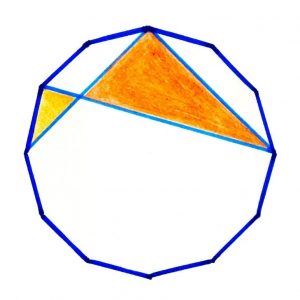
SOLUTION
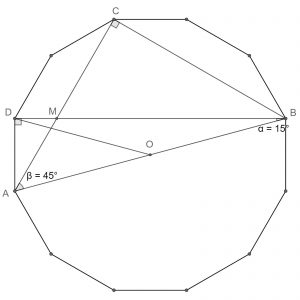
Let S be the area of the regular decagon.
The difference between the two areas is equal to the difference between the area of △ABC and the area of △ABD:
S(BCM)−S(AMD)=S(ABC)−S(ABD)
Since the hexagon is regular, we have that △ABD and △ABC are right-angle, and also ∠ABD=15° and ∠ABC=∠CAB=45°.
If AB=2R, then AD=22+3R,BD=22−3R,AC=BC=22R. Therefore, S(ABC)=4R2 and S(ABD)=2R2. If S(ABC)−S(ABD)=2, then 2R×R=2, and R=1. Finally, S=12S(AOD)=6S(ABD)=12.


Responses