An Ant's Path - Puzzle Prime

An Ant’s Path

An ant is positioned at one of the vertices of a cube and wants to get to the opposite vertex. If the edges of the die have length 1, what is the shortest distance the ant needs to travel?

SOLUTION

We unfold a cube to get a cross-shaped figure. Then, the problem is to find the shortest path between two points separated by a horizontal distance of 2 units and a vertical distance of 1 unit.

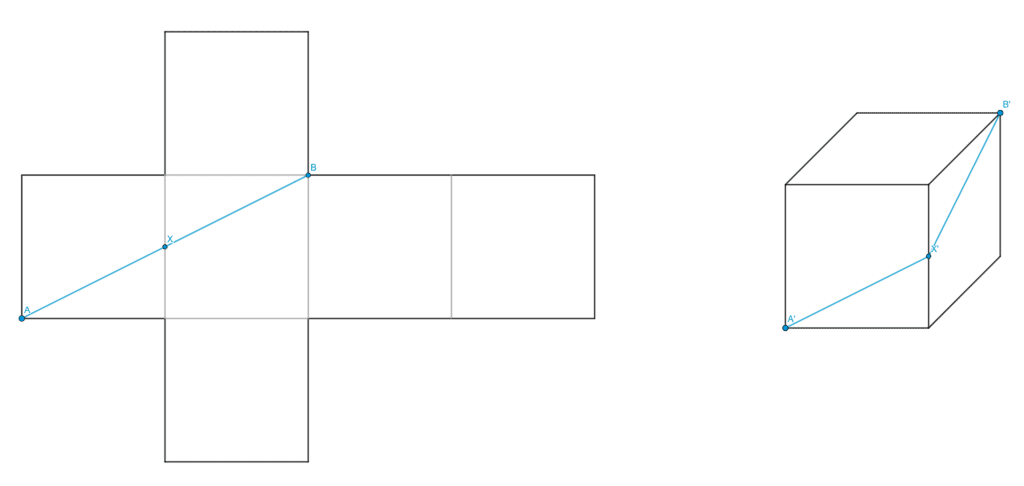
It is easy to see that the path in question is the one passing through the middle of the edge between the start and end points, and which has a distance of √5.

Unknown Author

We do not know where this puzzle originated from. If you have any information, please let us know via email.

Unknown Author

Puzzle Newsletter