Blue and Red Points
You have 100 blue and 100 red points in the plane, no three of which lie on one line. Prove that you can connect all points in pairs of different colors
SOLUTION
Connect the points in pairs of different colors so that the total length of all segments is minimal. If any two segments intersect, you can swap the two pairs among these four points and get a smaller total length.
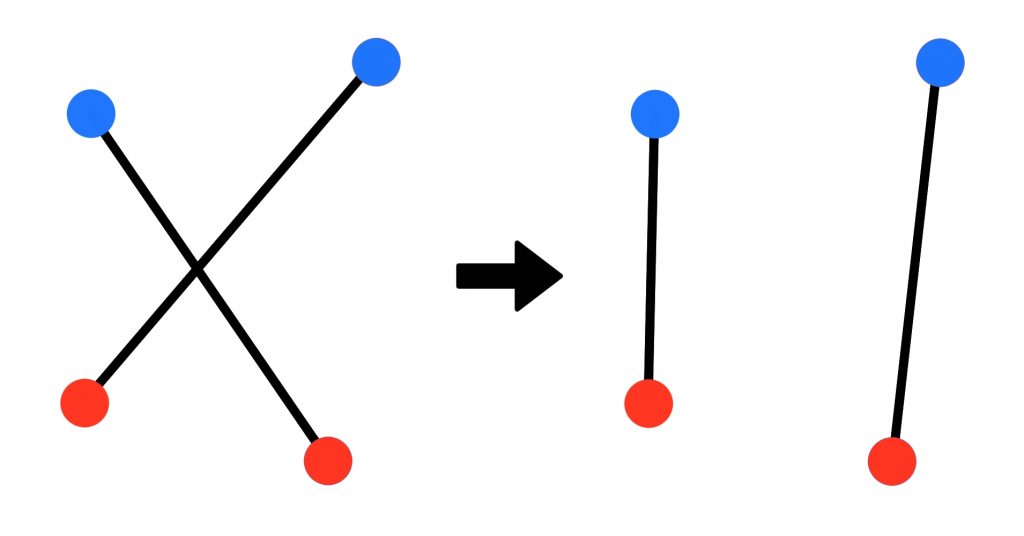
We do not know where this puzzle originated from. If you have any information, please let us know via email.


