Close the Loop
Alex and Bob are playing a game. They are taking turns drawing arrows over the segments of an infinite grid. Alex wins if he manages to create a closed loop, Bob wins if Alex does not win within the first 1000 moves. Who has a winning strategy if:
a) Alex starts first (easy)
b) Bob starts first (hard)
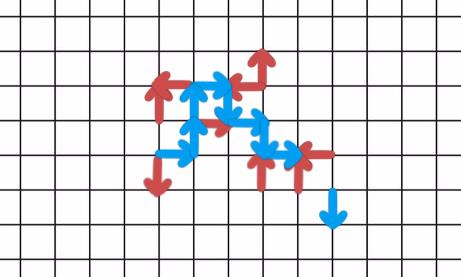
Remark: The loop can include arrows drawn both by Alex and Bob.
In both cases, Bob wins. An easy strategy for part a) is the following:
Every time Alex draws an arrow, Bob draws an arrow in such a way that the two arrows form an L-shaped piece and either point towards or away from each other. Since every closed loop must contain a bottom left corner, Alex cannot win.
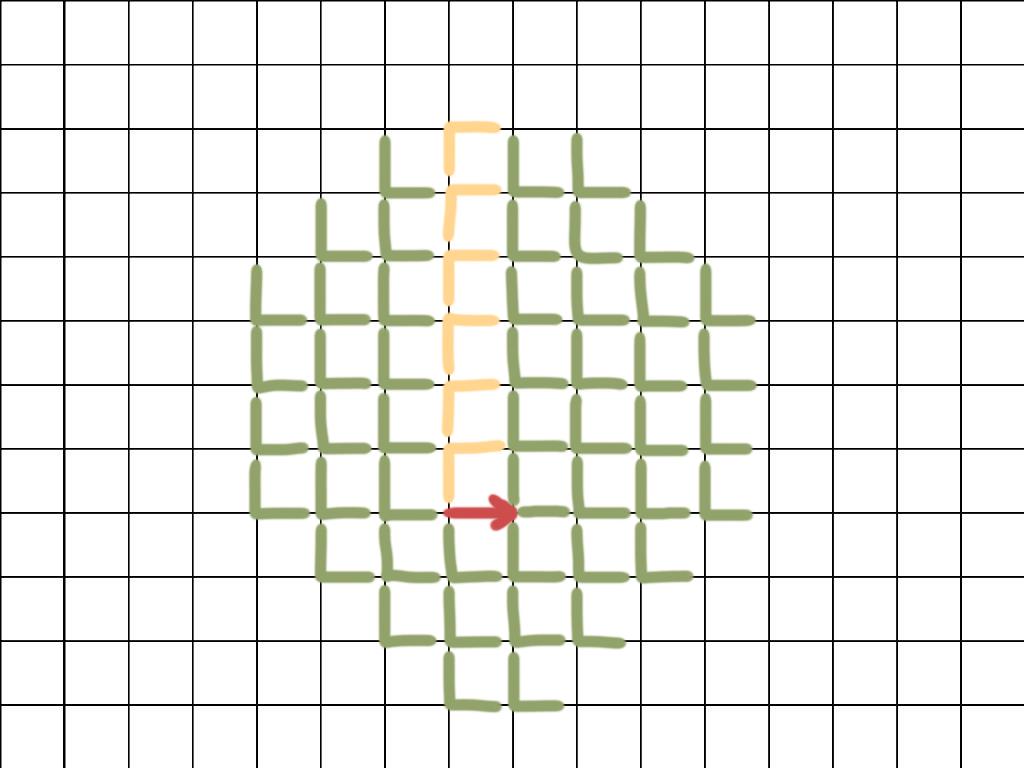
For part b), Bob should use a modification of his strategy in part a). First, he draws a horizontal arrow. Then, he splits the remaining edges into pairs, as shown in the image below. If Alex draws one arrow on the grid, then Bob draws its paired arrow, such that the two arrows point either towards or away from each other. The only places where a loop can have a bottom left corner are where Bob drew the first arrow or the grid points directly above it. However, if a loop has a bottom left corner there, then it is easy to see that it must have at least one more bottom left corner elsewhere, which is impossible.
We do not know where this puzzle originated from. If you have any information, please let us know via email.


