Tag: Featured

Puzzle Master at  | Website

Puzzle Prime is tirelessly looking all around the internet to find the very best puzzles and bring them all to puzzleprime.com.

FEATURED

Puzzle Tournament 4

Section: Contests Category: Tournament
Tags:

Puzzle Prime’s fourth puzzle tournament was organized on February 26, 2022. Congrats to REDCROUTONS who solved all the puzzles (even found a small mistake in one of them)!

REDCROUTONS

You have 60 minutes to solve 6 puzzles, each worth 1 point. Upload your solutions as a pdf, document, or image, using the form below. Good luck!

Time for work: 1 hour

Each problem is worth 1 point. Use the form at the bottom of the post to send your solutions.

1. The Grid

by Puzzle Prime

Figure out how the last portion (7×5 in yellow) of the grid should be colored in black and white.

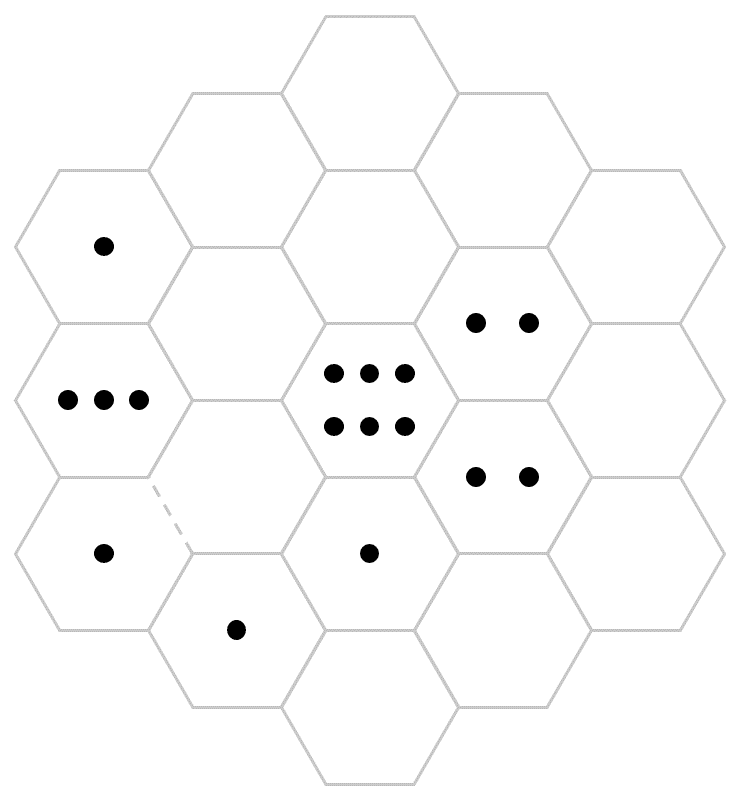
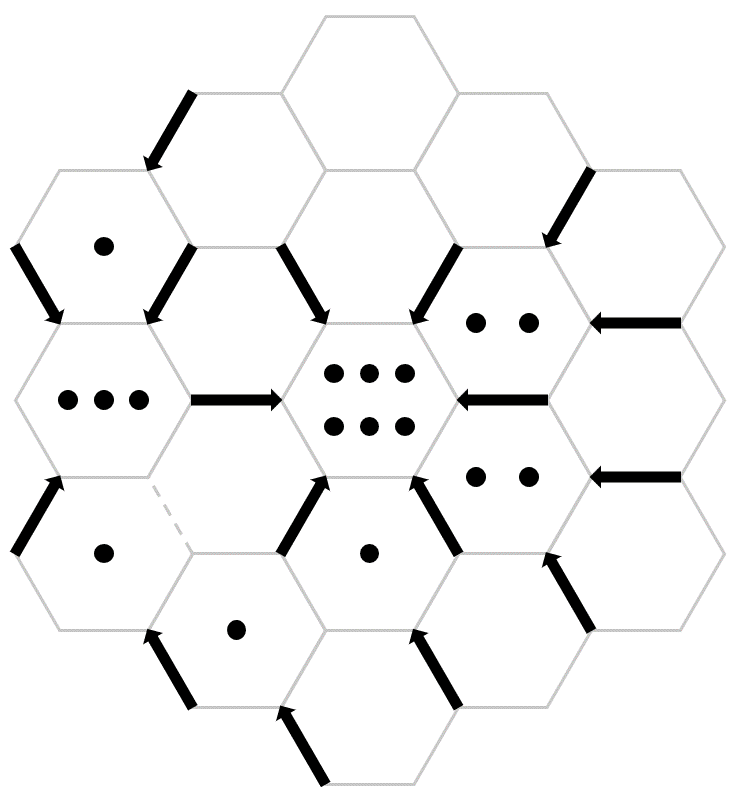
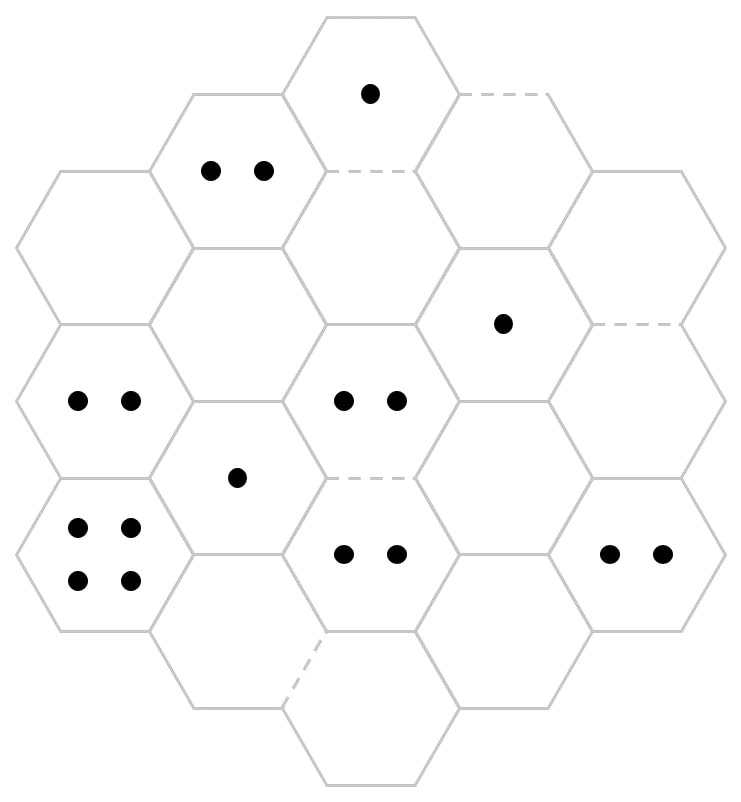
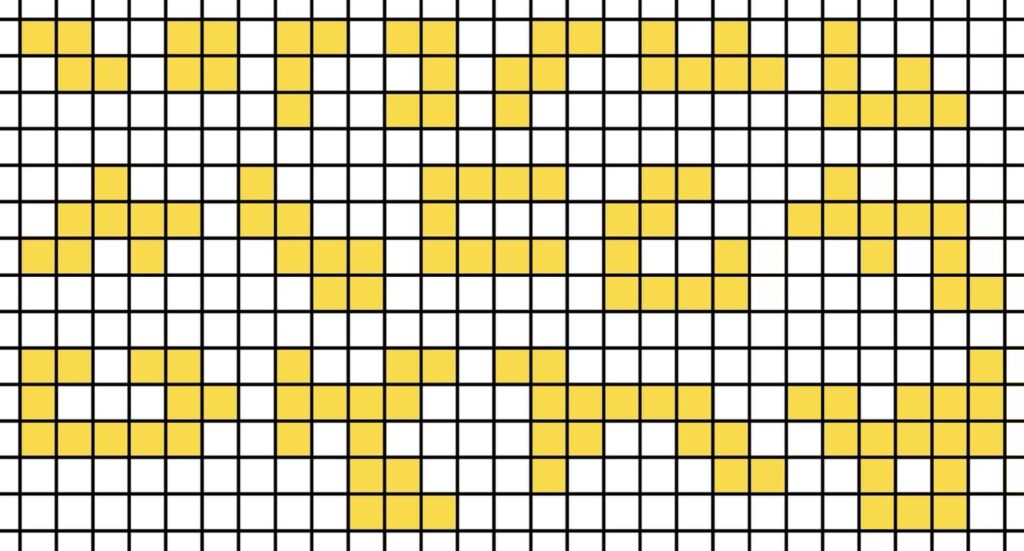
2. Hexado

by Dr. DJ Upton

Place arrows along hexagon edges so that the number of arrows pointing to each hexagon equals the number of dots inside, adhering to the following rules:

  1. Arrows cannot be touching.
  2. Arrows cannot be placed on dashed edges.
PUZZLE
SOLUTION

3. Segments

by Puzzle Prime

Use at most 27 segments to create the largest number with distinct digits.

Notes: For example, the number 273914 would use 5+3+5+6+2+4=25 segments.

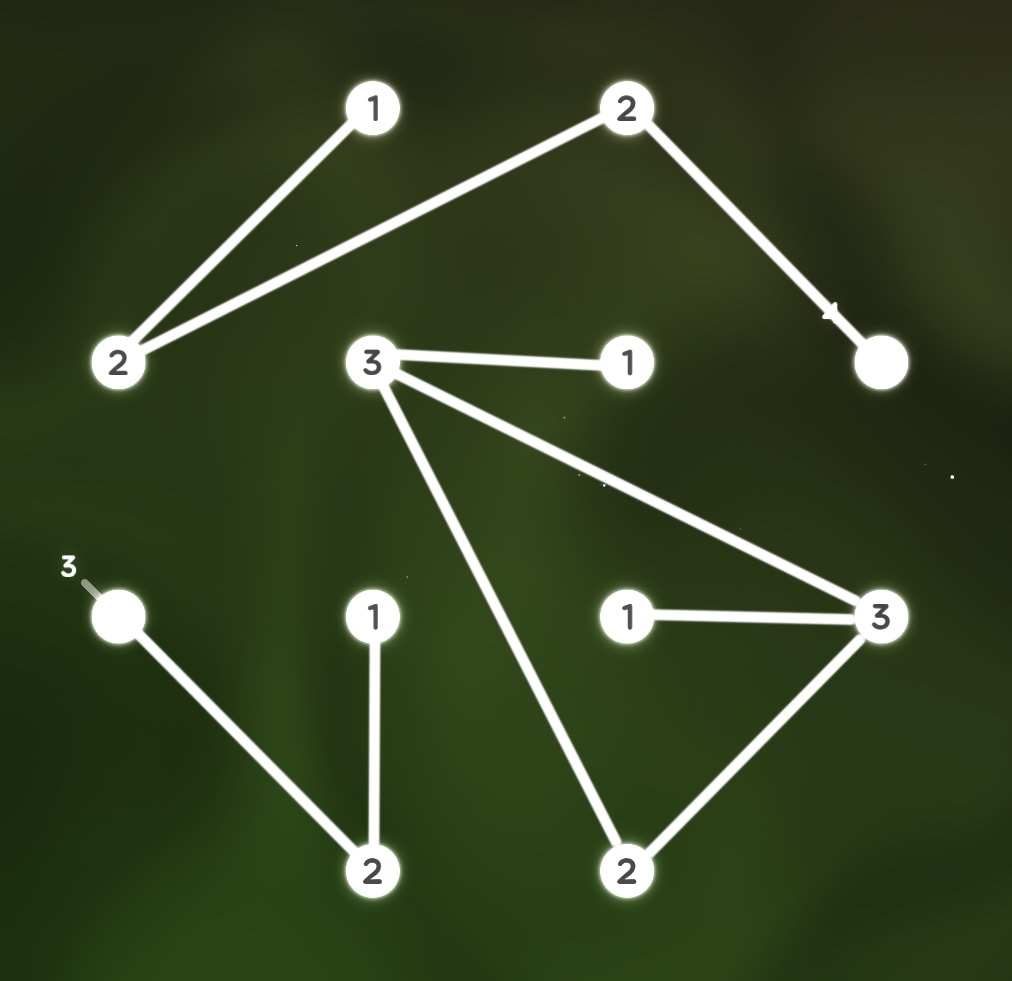
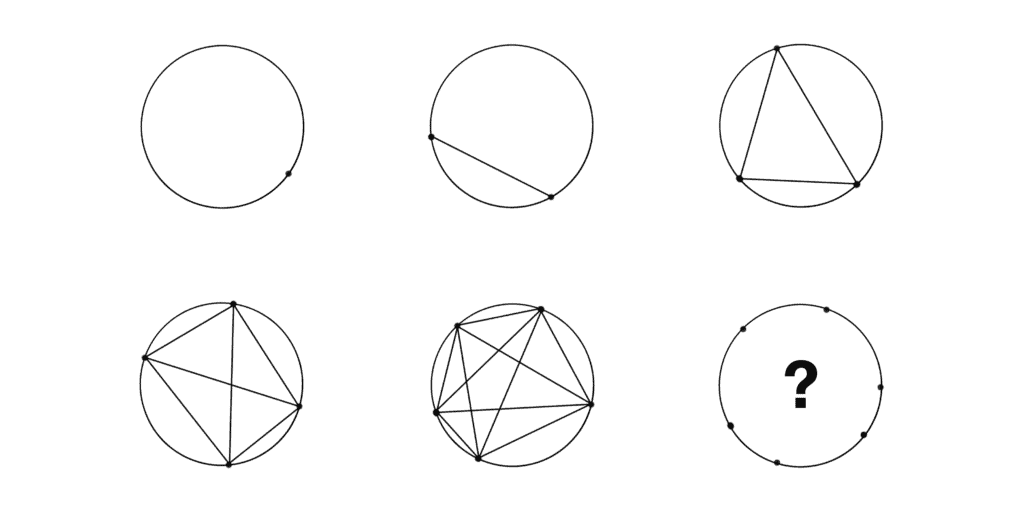
4. Constellations

by Raindrinker

Connect the stars with lines, so that the number inside each star corresponds to the number of lines connected to it, and the number outside each star corresponds to the total number of stars in its group.

Note: No line connecting two stars can pass through a third star.

PUZZLE
SOLUTION

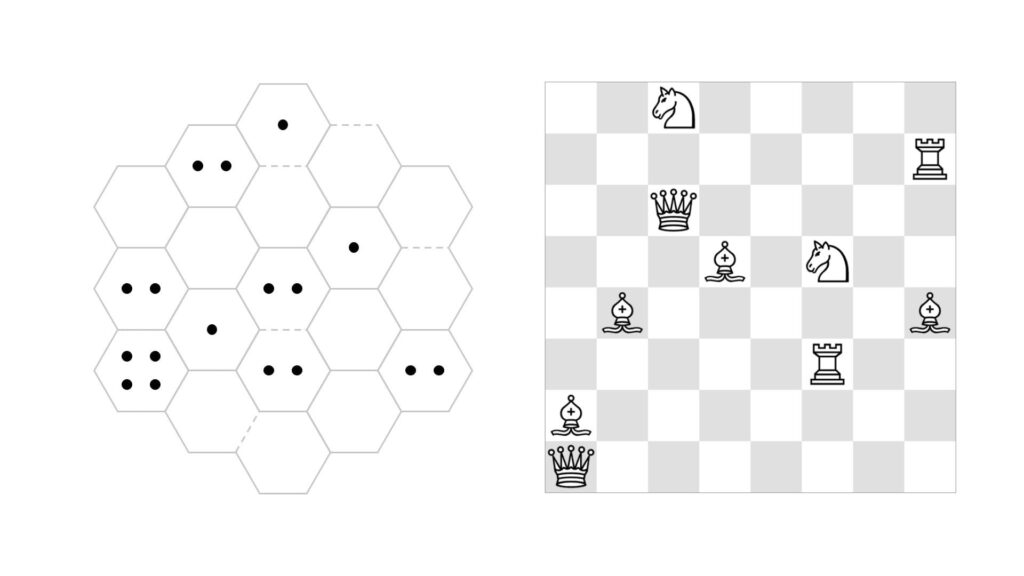
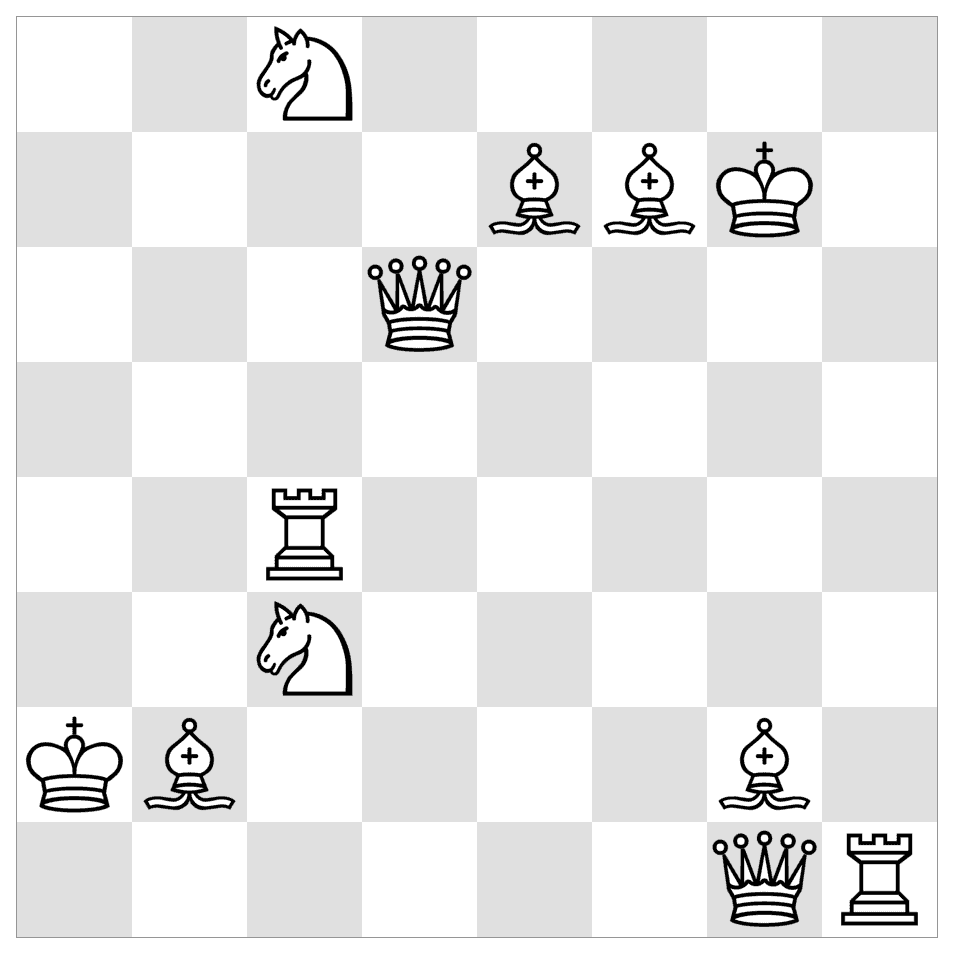
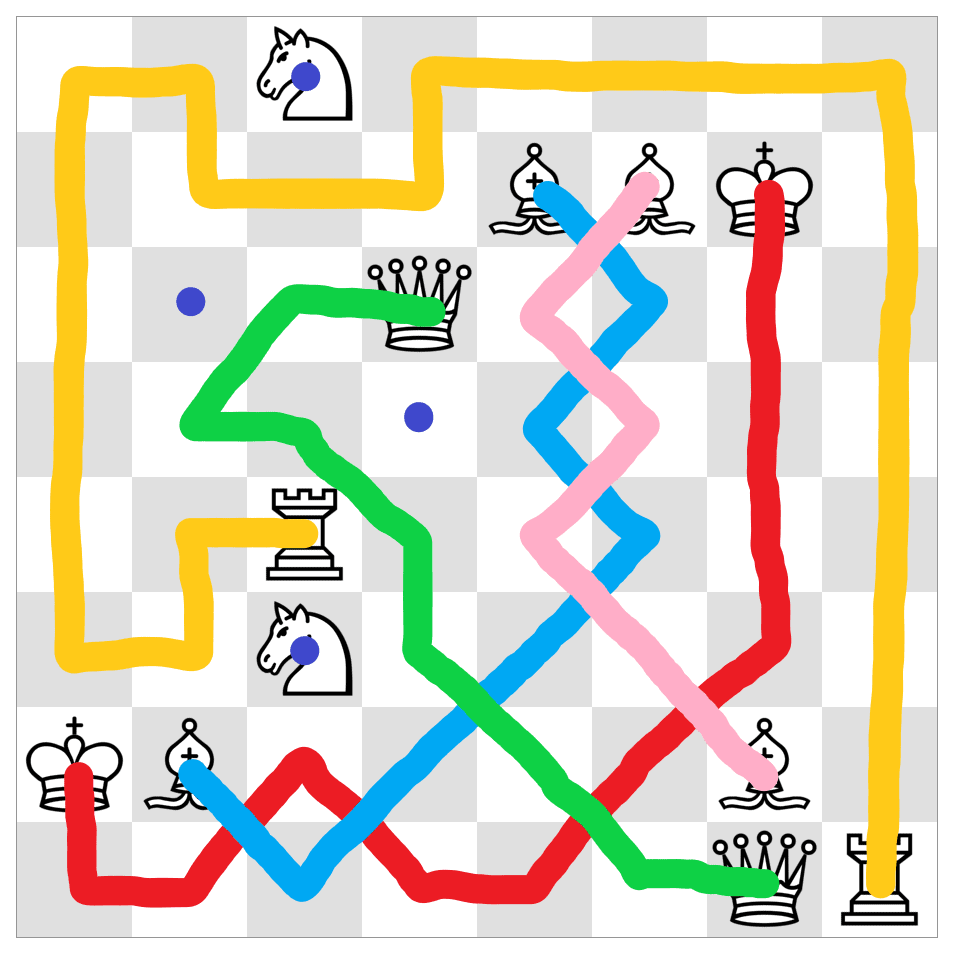
5. Chess Connect

by Puzzle Prime

The starting and ending positions of 6 chess pieces are shown on the board. Find the trajectories of the pieces, if you know that they do not overlap and completely cover the board.

Notes: The pieces can not backtrack. Two trajectories can intersect diagonally but can not pass through the same square. Only the Knight has a discontinuous trajectory.

PUZZLE
SOLUTION

6. Broken Square

by Puzzle Prime

Use exactly 5 out of these 16 pieces to build a 7×7 grid, without overlapping.

Note: You can rotate the pieces, but you cannot mirror them.

puzzle-prime
Puzzle Prime February 28, 2023
4 Comments
FEATURED

A Broken Circle

Section: Brain Teasers Category: Mathematics
Difficulty: Tags:

There are N points on a circle. If we draw all the chords connecting these points and no three of them intersect at the same point, in how many parts will the interior of the circle get broken?

For example, when N is equal to 1, 2, 3, 4, and 5, we get 1, 2, 4, 8, and 16 parts respectively.

The answer, somewhat surprisingly, is not 2ᴺ⁻¹, but 1 + N(N-1)/2 + N(N-1)(N-2)(N-3)/24.

In order to see that, we start with a single sector, the interior of the circle, and keep successively drawing chords. Every time we draw a new chord, we increase the number of parts by 1 and then add 1 extra part for each intersection with previously drawn chords.

Therefore, the total number of parts at the end will be:

1 + the number of the chords + the number of the intersections of the chords

Each chord is determined by its 2 endpoints and therefore the number of chords is N(N-1)/2.

Each intersection is determined by the 4 endpoints of the two intersecting chords and therefore the number of intersections is N(N-1)(N-2)(N-3)/4!.

unknown-author
Unknown Author January 13, 2023
0 Comments
FEATURED

The Bicycle Problem

Section: Brain Teasers Category: Science
Difficulty: Tags:

If you pull straight back on a pedal of a bicycle when it is at its lowest position, will the bicycle move forward or backward?

The surprising answer is that (usually) the bicycle will move backward.

When a bicycle moves forward, the trajectory its pedal traces with respect to the ground is called a trochoid. Depending on the selected gear of the bicycle, that trochoid could be:

  1. Curtate trochoid (for almost all gears of most bicycles)
  2. Prolate trochoid (if the gear is very low and the bicycle moves slowly)
  3. Common trochoid, a.k.a. cycloid (if the wheels of the bicycle and the pedal spin at identical speeds, practically never happens)
curtate trochoid
prolate trochoid
common trochoid (cycloid)

Since we are fixed with respect to the ground, by pulling the pedal backward, we are causing it to move leftward along the trochoid and therefore the bicycle will be moving backward. We note that despite that, the pedal will be moving forward with respect to the bicycle (but not with respect to the ground).

You can see a visual explanation of this puzzle in the video below.

unknown-author
Unknown Author January 1, 2023
2 Comments
FEATURED

Sum Up to 15

Section: Brain Teasers Category: Mathematics
Difficulty: Tags:

Tango and Cash are playing the following game: Each of them chooses a number between 1 and 9 without replacement. The first one to get 3 numbers that sum up to 15 wins. Does any of them have a winning strategy?

Place the numbers from 1 to 9 in a 3×3 grid so that they form a magic square. Now the game comes down to a standard TIC-TAC-TOE, and it is well-known that it always leads to a draw when both players use optimal strategies.

unknown-author
Unknown Author July 25, 2022
6 Comments
FEATURED

David Copperfield

Section: Brain Teasers Category: Mathematics
Difficulty: Tags:

David Copperfield and his assistant perform the following magic trick. The assistant offers a person from the audience to pick 5 arbitrary cards from a regular deck and then hands them back to him. After the assistant sees the cards, he returns one of them to the audience member and gives the rest one by one to David Copperfield. After the magician receives the fourth card, he correctly guesses what card the audience member holds in his hand. How did they perform the trick?

Out of the five cards, there will be (at least) two of the same suit; assume they are clubs. Now imagine all clubs are arranged in a circle in a cyclic manner – A, 2, 3, … J, Q, K (clock-wise), and locate the two chosen ones on it. There are two arks on the circle which are connecting them and exactly one of them will contain X cards, with X between 0 and 5. Now the assistant will pass to David Copperfield first the clubs card which is located on the left end of this ark, will return to the audience member the clubs card which is located on the right end of it and, with the remaining three cards, will encode the number X. In order to do this, he will arrange the three extra cards in increasing order – first clubs A-K, then diamonds A-K, then hearts A-K and finally spades A-K. Let us call the smallest card in this order “1”, the middle one “2” and the largest one “3”. Now, depending on the value of X, the assistant will pass the cards “1”, “2” and “3” in the following order:

X=0 ⇾ 1, 2, 3
X=1 ⇾ 1, 3, 2
X=2 ⇾ 2, 1, 3
X=3 ⇾ 2, 3, 1
X=4 ⇾ 3, 1, 2
X=5 ⇾ 3, 2, 1

In this way David Copperfield will know the suit of the audience member’s card and also with what number he should increase the card he received first in order to get value as well. Therefore, he will be able to guess correctly.

unknown-author
Unknown Author July 22, 2022
2 Comments
FEATURED

Gerrymandering

Section: Brain Teasers Category: Deduction
Difficulty: Tags:

The city has 49 districts that vote for blue, yellow, or purple as shown in the grid. Seven electoral regions are drawn up to elect a city council. Each region consists of seven districts and each region will elect one councilor. Can you gerrymander the map so that blue will win the majority?

The solution is shown below.

art-of-play
Art of Play June 22, 2022
0 Comments
FEATURED

Domino and Chess

Section: Brain Teasers Category: Insight
Difficulty: Tags:

Can you cover the chess board with 31 domino pieces, such that only two opposite corners are left uncovered?

The answer is NO. Every domino piece covers exactly one black and one white square on the chess board. Since initially you start with a different number of available white and black squares on the chess board, it is impossible to cover it with domino pieces.

unknown-author
Unknown Author May 19, 2022
2 Comments
FEATURED

Shark Attack

Section: Brain Teasers Category: Mathematics
Difficulty: Tags:

A man stands in the center of a circular field which is encompassed by a narrow ring of water. In the water there is a shark which is swimming four times as fast as the man is running. Can the man escape the field and get past the water to safety?

Yes, he can. Let the radius of the field is R and its center I. First the man should start running along a circle with center I and radius slightly less than R/4. His angular speed will be larger than the angular speed of the shark, so he can keep running until gets opposite to it with respect to I. Then, the man should dash away (in a straight line) towards the water. Since he will need to cover approximately 3R/4 distance and the shark will have to cover approximately 3.14R distance, the man will have enough time to escape.

unknown-author
Unknown Author April 25, 2022
2 Comments

Report

Harassment or bullying behavior
Contains mature or sensitive content
Contains misleading or false information
Contains abusive or derogatory content
Contains spam, fake content or potential malware

Block Member?

Please confirm you want to block this member.

You will no longer be able to:

  • Mention this member in posts
  • Message this member
  • Add this member as a connection

Please note: This action will also remove this member from your connections and send a report to the site admin. Please allow a few minutes for this process to complete.

Report

You have already reported this .